
- •Раздел 2. Элементы векторной алгебры
- •1. Определение вектора
- •2. Направление вектора. Коллинеарность векторов
- •Свойства коллинеарных векторов:
- •3. Абсолютная величина вектора
- •4. Равенство векторов
- •5. Линейные операции над векторами
- •5.1. Сложение векторов
- •Свойства сложения:
- •5.2. Вычитание векторов
- •5.3. Умножение вектора на действительное число
- •Свойства произведения вектора на число
- •6. Векторное пространство
- •7. Линейная зависимость векторов
- •Свойства линейно зависимых векторов:
- •8. Базис системы векторов и пространства
- •Свойства базиса системы векторов:
- •9. Координаты вектора в базисе
- •Свойства координат векторов:
- •Практикум 13. Векторы. Основные понятия. Линейные операции
- •2) Выполнить оставшиеся номера
9. Координаты вектора в базисе
Теорема 7.3.
Любой
вектор
![]() пространства раскладывается по базису
пространства раскладывается по базису
![]() единственным
образом:
единственным
образом:
![]() . (7.10)
. (7.10)
Определение 23.
Коэффициенты
аx,
аy,
аz
разложения вектора по базисным ортам
![]() называются координатами
вектора в данном базисе.
называются координатами
вектора в данном базисе.
![]() .
.
Координаты есть проекции вектора на соответствующие оси координат.
Свойства координат векторов:
Пусть
![]() ,
,
![]() ,
,
![]() .
Тогда
.
Тогда
1.
![]()
2.
![]()
3.
![]() (7.11)
(7.11)
4. Условие
коллинеарности векторов:
векторы
![]() и
и
![]() ,
коллинеарны тогда и только тогда, когда
их одноименные координаты пропорциональны:
,
коллинеарны тогда и только тогда, когда
их одноименные координаты пропорциональны:
![]() . (7.12)
. (7.12)
Пример 4. Выяснить, образуют ли
векторы
![]() ,
,
![]() ,
,
![]() базис.
базис.
Решение. Система векторов образует
базис, если она линейно независима, т.е.
равенство
![]() справедливо только при
справедливо только при
![]() .
.
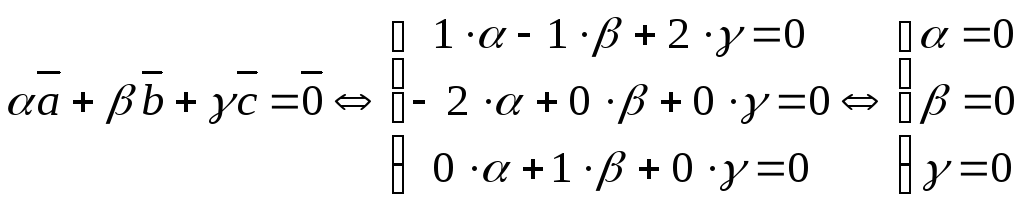 .
Значит, векторы образуют базис.
.
Значит, векторы образуют базис.
Практикум 13. Векторы. Основные понятия. Линейные операции
-
Задача 1 (Элементы векторной алгебры. С.7)
-
Задача 2 (ЭВА. С.7)
-
В треугольнике АВС сторона АВ точками M и N разделена на части: АМ=MN=NB. Найдите вектор
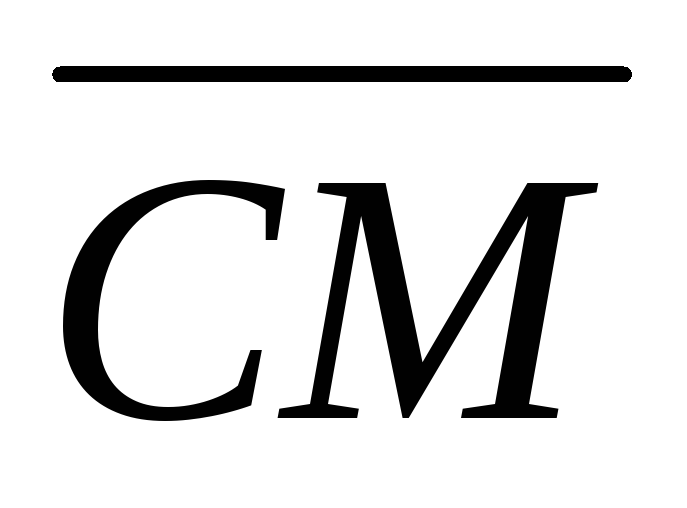 ,
если
,
если
 ,
,
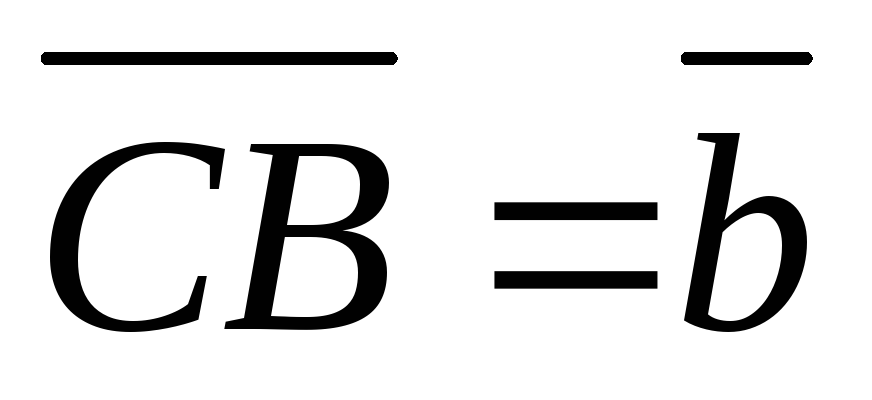 .
. -
В треугольнике АВС сторона АМ – биссектриса угла ВАС, причем точка М лежит на стороне ВС. Найдите вектор
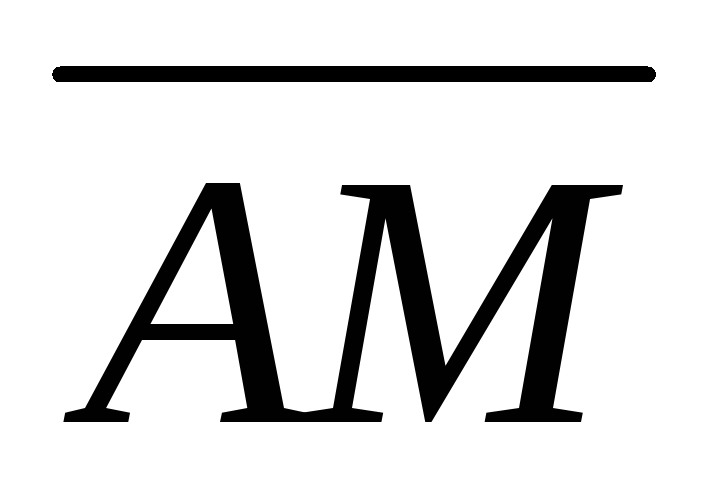 ,
если
,
если
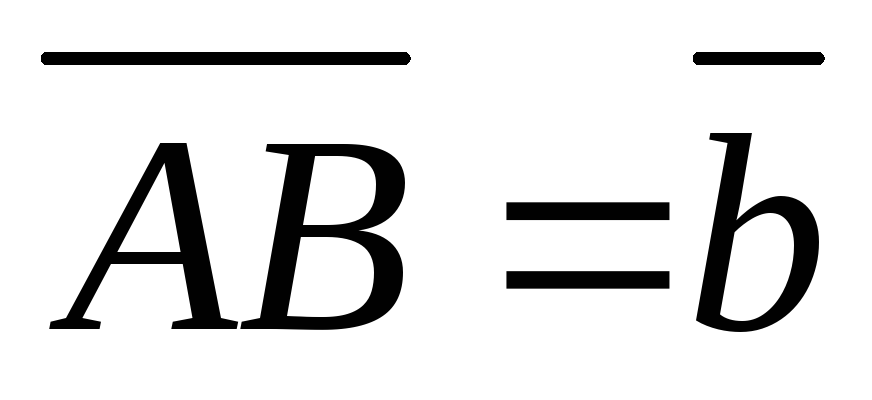 ,
,
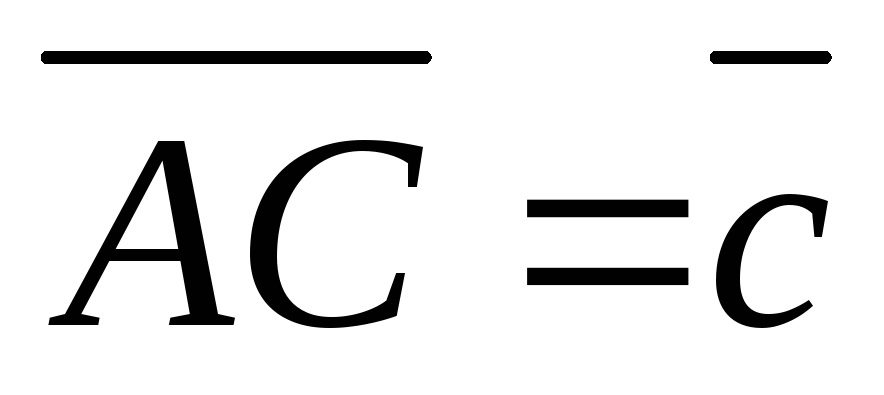 .
. -
Пример 7 (ЭВА. С.9)
-
Пример 9 (ЭВА. С.11)
-
Пример 8 (ЭВА. С.10)
-
Найдите линейную комбинацию векторов
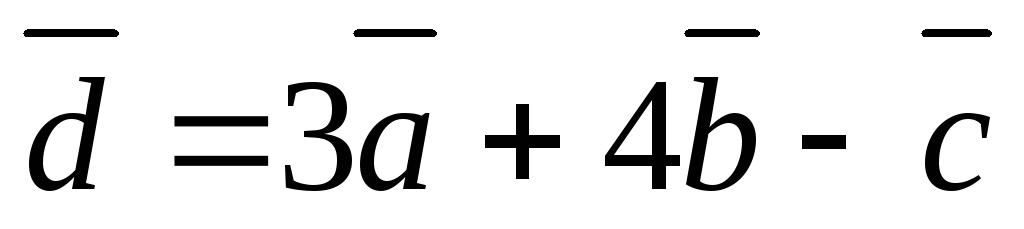 ,
где
,
где
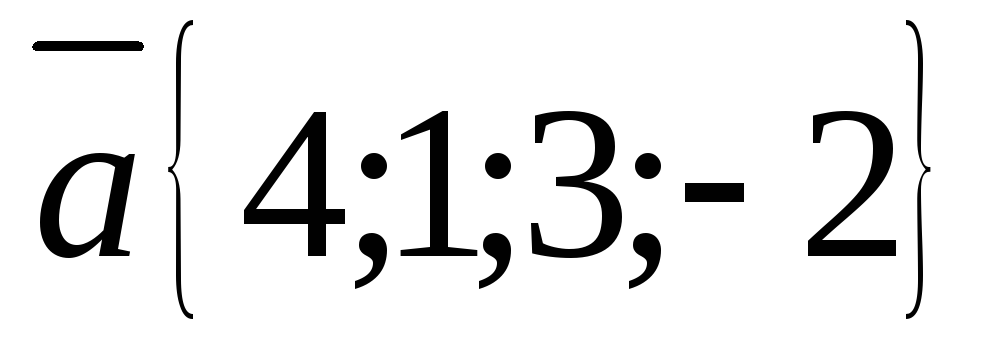 ,
,
 ,
,
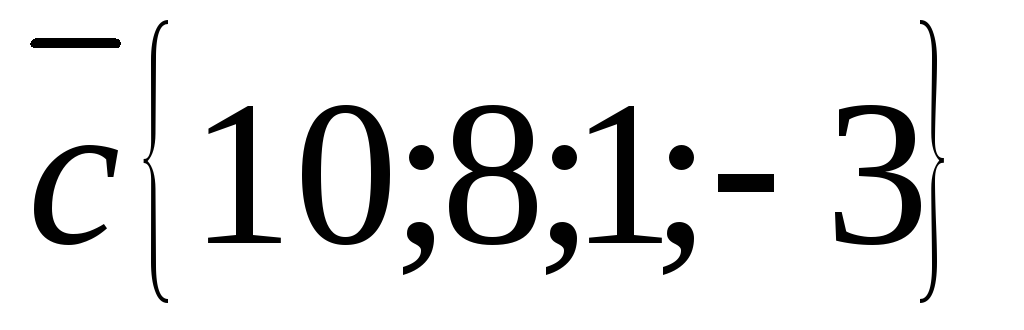 .
. -
Вычислите координаты линейной комбинации векторов
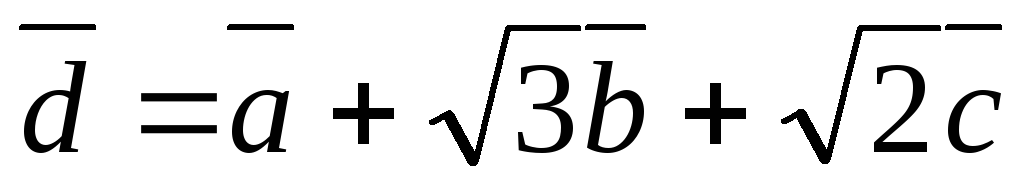 ,
где
,
где
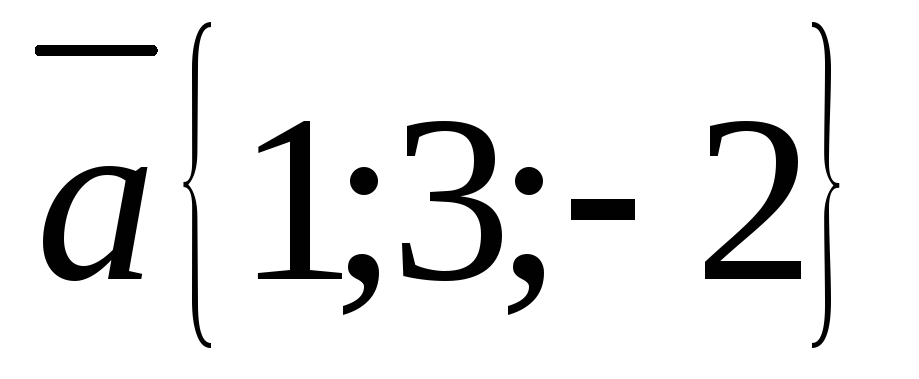 ,
,
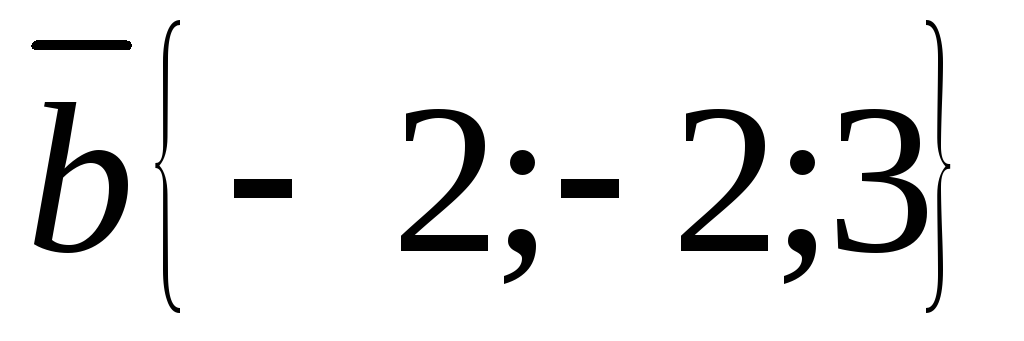 ,
,
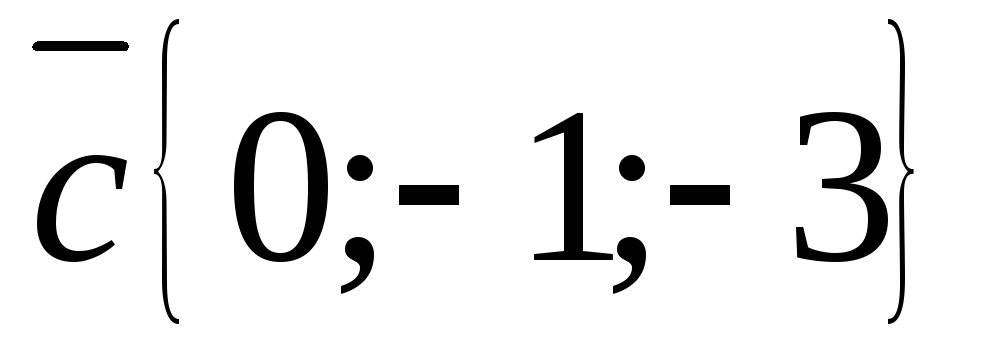 .
. -
Вычислите координаты вектора
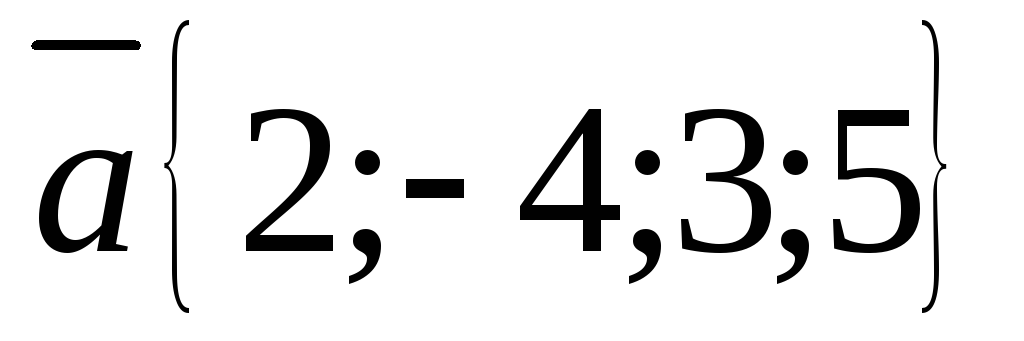 в базисе
в базисе
 ,
где
,
где
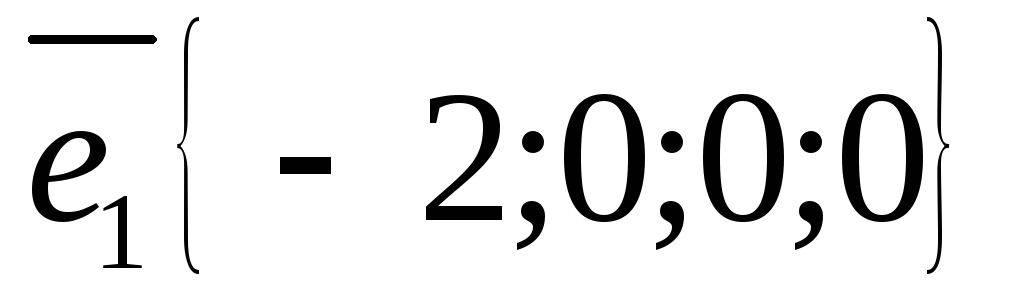 ,
,
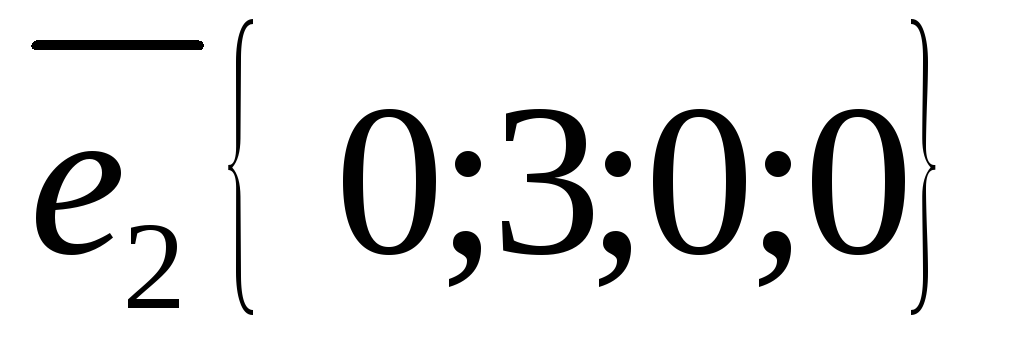 ,
,
 ,
,
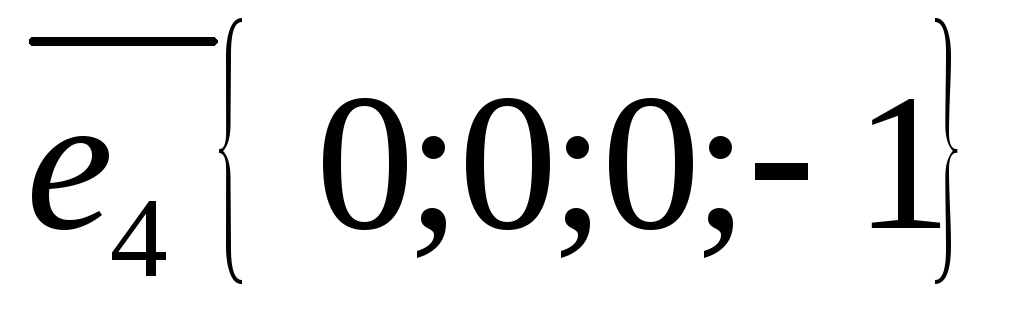
-
Выясните, является ли система векторов линейно независимой
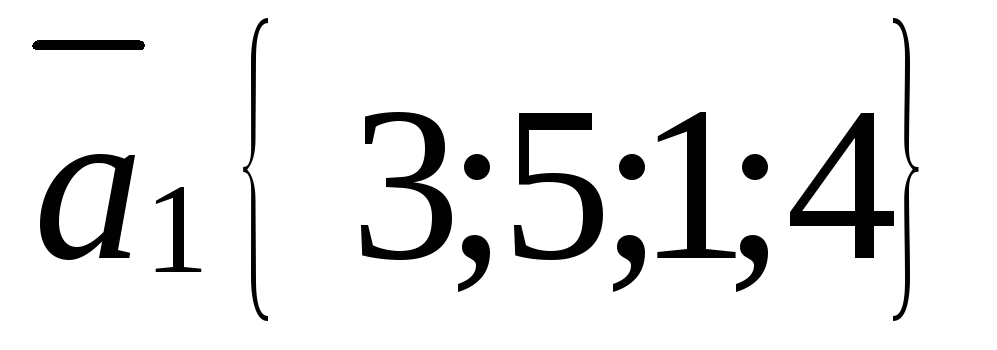 ,
,
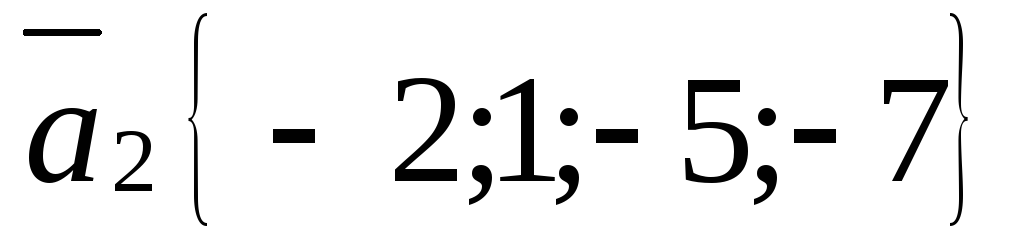 ,
,
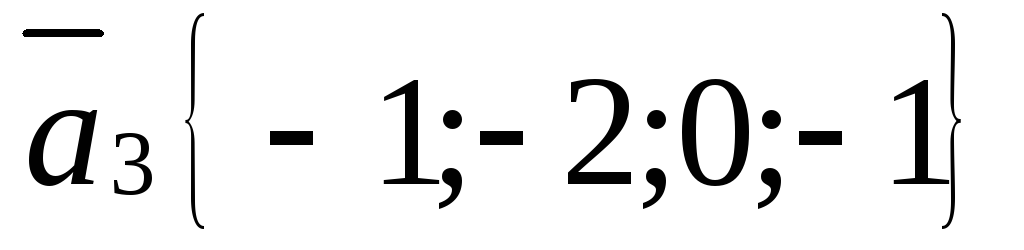 .
.
-
Выясните, является ли система векторов линейно независимой
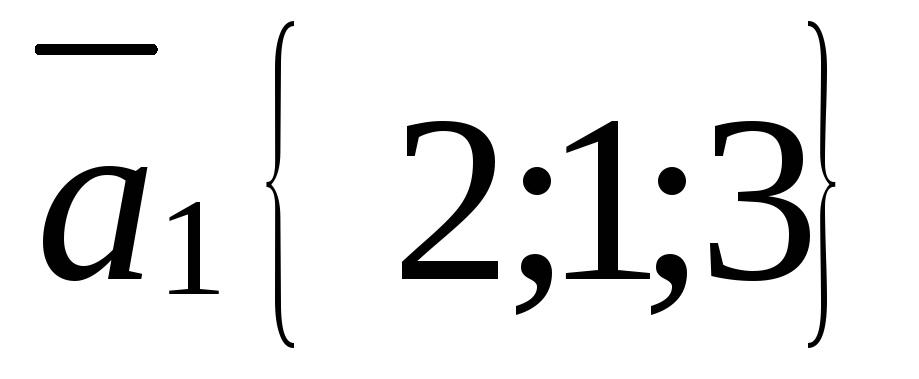 ,
,
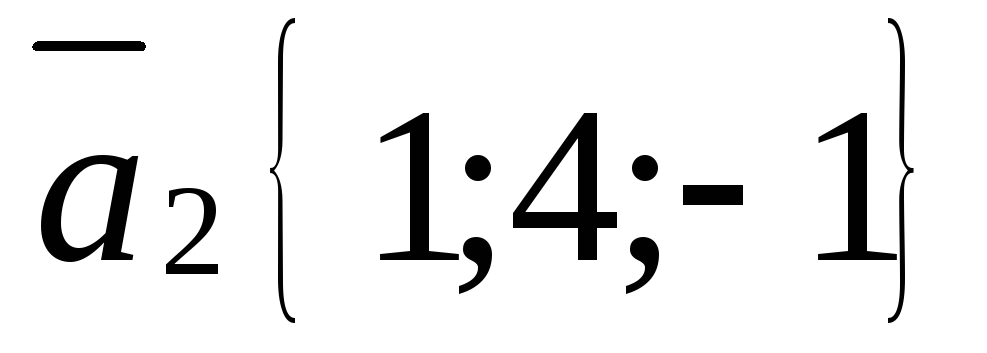 ,
,
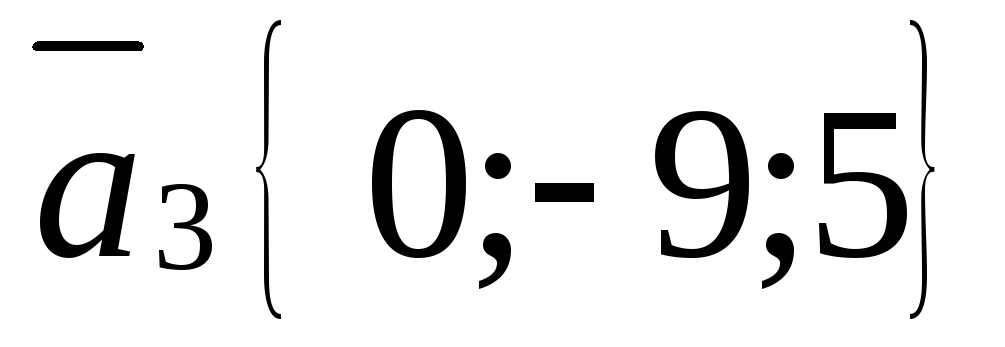 .
.
-
Даны векторы
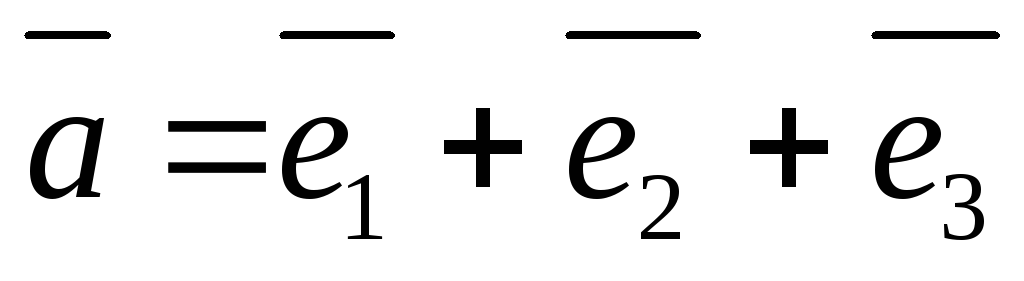 ,
,
 ,
,
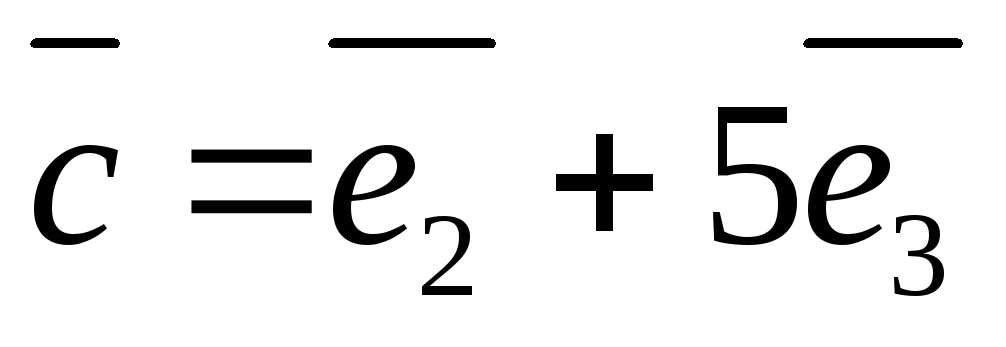 в базисе
в базисе
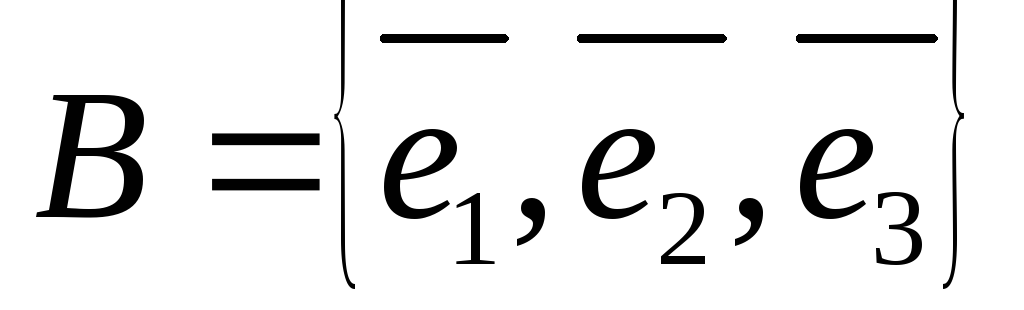 .
Докажите, что векторы
.
Докажите, что векторы
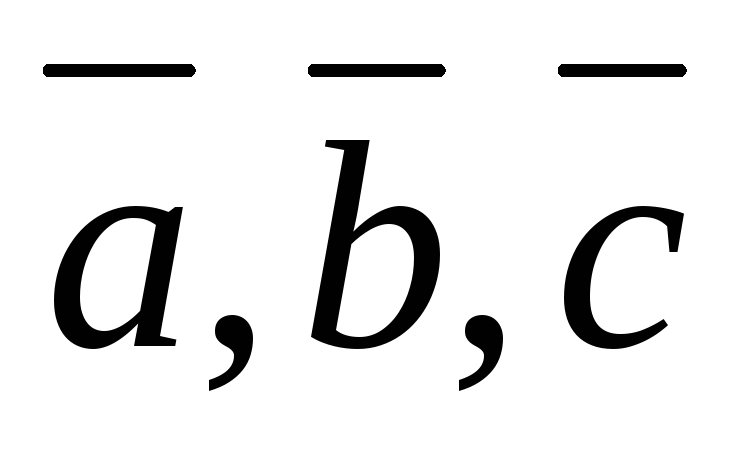 образуют базис. Вычислите координаты
вектора
образуют базис. Вычислите координаты
вектора
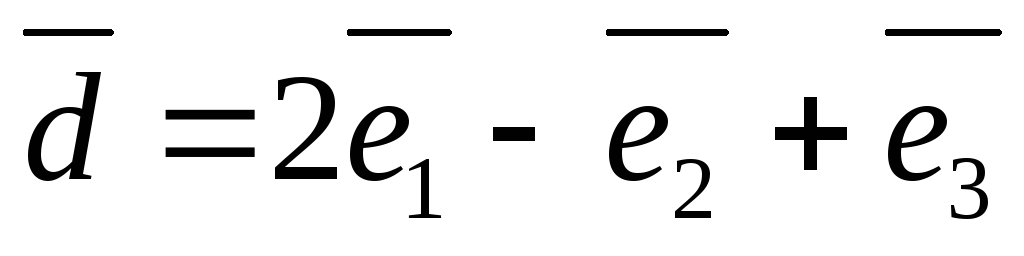 в базисе
в базисе
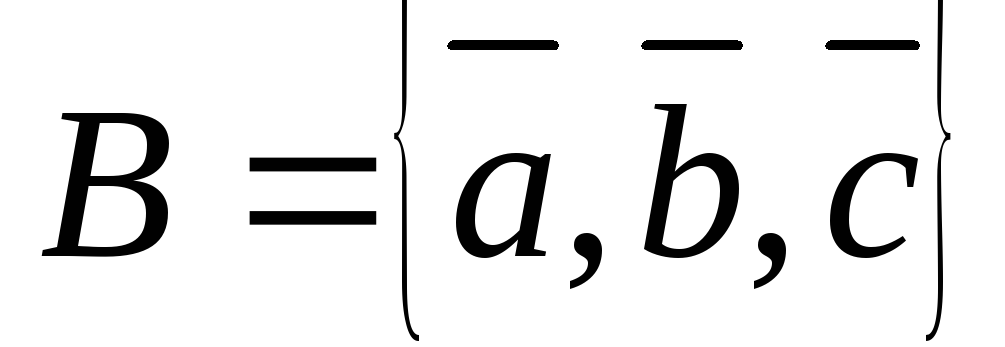
-
Выясните, раскладывается ли вектор
 через векторы системы:
через векторы системы:
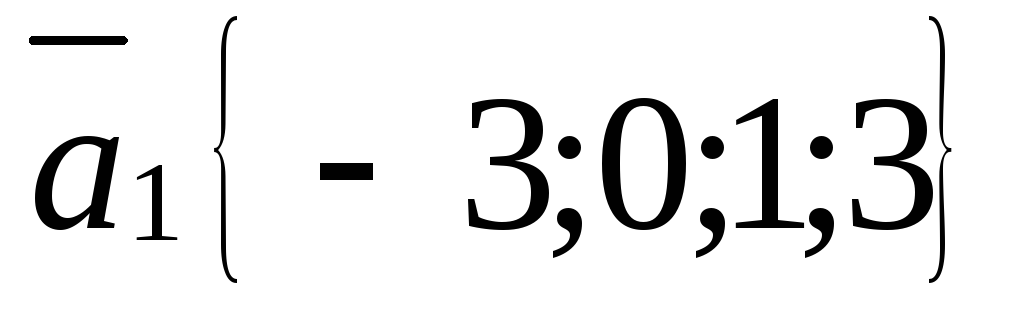 ,
,
 ,
,
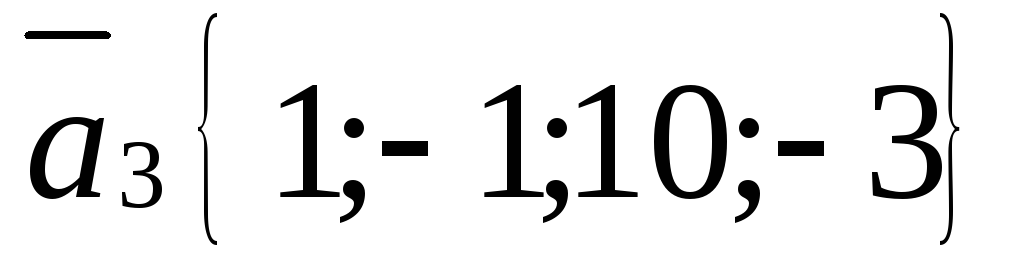 .
.
-
Выясните, раскладывается ли вектор
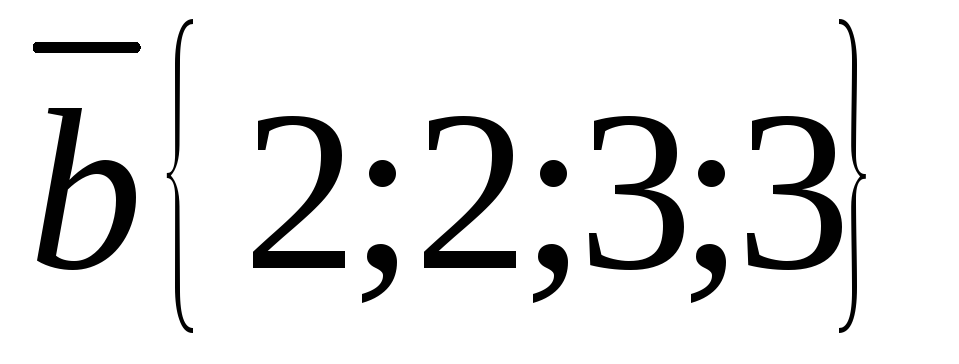 через векторы системы:
через векторы системы:
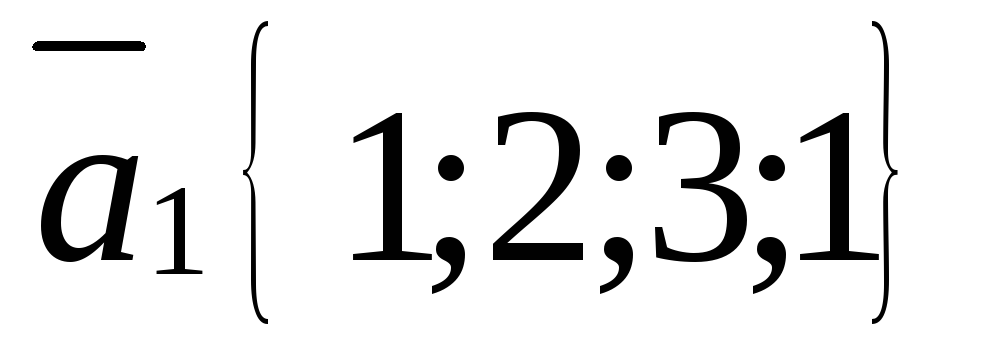 ,
,
 ,
,
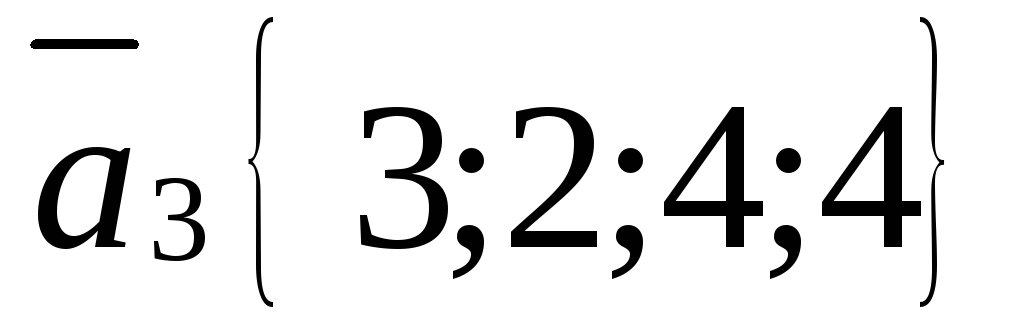 .
.
Д/з: 1) Повторить теорему о коллинеарных векторах, теорему о компланарных векторах,
2) Выполнить оставшиеся номера
