Раздел 2. Элементы векторной алгебры
Лекция 7. ВЕКТОРы. Линейные операции над векторами
Вопросы.
-
Определение геометрического вектора. Нулевой вектор.
-
Направление вектора. Противоположный вектор. Коллинеарные, противоположно направленные и одинаково направленные векторы.
-
Длина вектора. Длина нулевого вектора. Равенство векторов.
-
Сложение векторов. Свойства сложения векторов. Правила треугольника, параллелограмма, многоугольника. Вычитание векторов.
-
Умножение вектора на действительное число. Свойства умножения вектора на число.
-
Понятие о векторном пространстве.
-
Линейная комбинация векторов. Линейная зависимость системы векторов. Компланарные векторы.
-
Базис системы векторов. Ортогональный базис. Ортонормированный базис.
-
Координаты вектора в базисе. Свойства координат векторов: сложение, вычитание и умножение вектора на число. Необходимое и достаточное условие коллинеарности двух векторов в координатах.
1. Определение вектора
Определение 1.
Вектором называется направленный отрезок, т.е. отрезок, для которого указано какая из концевых его точек считается первой, какая – второй. Первая точка направленного отрезка называется началом вектора, а вторая точка – концом.
В тексте вектор
записывается двумя заглавными буквами
латинского алфавита с чертой наверху,
например,
или
.
Вектор
вполне определяется упорядоченной
парой точек, первая из которых – точка
A
– называется его началом,
а вторая – B
– его концом.
Определение 2.
Вектор, начало и конец которого совпадают, называется нулевым.
.
Существуют различные типы векторов, например свободные, скользящие, связные (фиксированные). Иногда, вместо того, чтобы рассматривать в качестве векторов множество направленных отрезков, берут только его подмножества:
свободные – равные по длине и направлению направленные отрезки,
скользящие – направленные отрезки, равные в смысле свободных векторов, начала и концы которых расположены на одной прямой,
связные (фиксированные) – направленные отрезки с общим началом.
Например, векторы
,
,
или
и
.
Теорема 7.1.
Для любых точки
пространства О
и вектора
существует единственная точка М
такая, что
=
.
Построение точки
М
называют откладыванием
вектора
от
точки
О.
Эта операция позволяет рассматривать
любой вектор независимо от положения
его начала в пространстве. Будем помнить,
что любой вектор определяется двумя
компонентами:
– направлением,
– длиной.
2. Направление вектора. Коллинеарность векторов
Определение 3.
Векторы
и
называются коллинеарными,
если существует прямая, которой они
параллельны. Обозначается
||
.
П
римечание.
В школьном учебнике коллинеарность
рассматривается для определения вектора
как направленного отрезка. Два вектора
и
называются
коллинеарными,
если они лежат на одной и той же прямой
или на параллельных прямых.
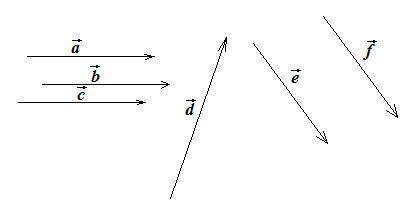
Пример 1. Перечислите коллинеарные векторы.
Векторы
и
коллинеарны,
и
коллинеарны,
и
не коллинеарны.
Пример 2. Дана трапеция ABCD с основаниями ВС и AD.
Докажите, что
векторы
и
коллинеарны.
Для решения достаточно показать, что существует прямая ВС,
которой оба вектора параллельны.