34

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Государственное образовательное учреждение

Высшего профессионального образования

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ЭКОНОМИКИ И ФИНАНСОВ

Кафедра Математики и Информатики

Метеодические указания и контрольные задания

По дисциплине «Математика»

Для студентов 1 курса заочного отделения

Часть 1

Издательство

Санкт-Петербургский государственный университет

экономики и финансов

2010

Утверждены методическим советом университета

Методические указания и контрольные задания по курсу высшей математики для студентов I курса заочного факультета. - СПб.:Изд-во СПбГУЭФ, 2010,-34 с.

Составители: асс.И.В.Кондратьева, доц И.К.Лицкевич,

асс. К.С.Мамаева, асс. Л.Р.Пуховская,

доц. Е.З.Хотимская

Рецензенты: доц.А.И.Плоткин, доц. А.А.Тамонов

Над новым изданием работали:

доц.Е.Н.Евстафьев, асс. М.В.Галактионова.

© Издательство Санкт-Петербургского университета экономики и финансов, 2010.

Обучение на заочном факультете требует от студента самостоятельного изучения материала, предусмотренного программой. Результаты этой работы оцениваются на экзамене. Практические навыки в решении задач, необходимые для успешной сдачи экзамена, проверяются при защите контрольной работы. В помощь студентам по теоретическим основам курса читаются установочные лекции, а примеры решения типовых задач приводятся в предлагаемых методических указаниях.

Правила выполнения и защиты контрольной работы изложены в конце данного пособия.

Программа первого семестра включает изучение двух разделов курса:

1. Аналитическая геометрия и элементы векторной алгебры.

2. Линейная алгебра.

Раздел I. Аналитическая геометрия и элементы векторной алгебры.

Напоминаем кратко некоторые основные сведения из данного раздела.

1. Прямоугольные координаты на плоскости и в пространстве. В заданной системе координат каждой точке М плоскости соответствует упорядоченная пара чисел (х,у) – координаты точки и, обратно, каждой паре чисел (х,у) соответствует единственная точка М плоскости хОу. Если же точка М задана в пространстве, то она определяется тремя координатами (х,у,z).

Расстояние d=|М1,М2| между двумя точками М1(х₁,у₁) и М2(х₂,у₂) на плоскости вычисляется по формуле:

d =. (1)

Для точек М1(х₁,у₁,z₁) и М2(x₂,y₂,z₂), заданных в пространстве справедлива аналогичная формула:

d =.

Зная координаты концов А(х_А,у_А,z_A) и B(x_B,y_B,z_B) отрезка АВ, можно найти координаты точки М(x_M,y_M,z_M), которая делит данный отрезок в отношении , по формулам

х_м=; у_м=; z_м=. (2)

В частности, если точка М является серединой отрезка АВ , т.е. |АМ|=|МВ|, то , и формула (2) примет вид:

х_м=; у_м=; z_м=. (3)

Пример 1. В треугольнике с вершинами А(-2,0), В(6,6), С(1,-4) определить длины медианы AD и биссектрисы АЕ.

Решение. а) Так как AD медиана, то точка D делит отрезок ВС пополам, следовательно . Координаты точки D найдем по формуле (3)

х_D= =

у_D= = 1

По формуле (1) находим длину медианы AD:

|AD| = .

б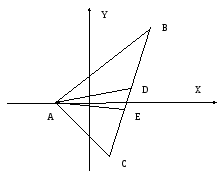) Для того, чтобы вычислить длину биссектрисы надо найти координаты точки Е. Напомним, что биссектриса делит противолежащую сторону на части, пропорциональные прилежащим сторонам, т.е. .

Следовательно, надо вычислить и |А|. По формуле (1), подставляя соответствующие координаты получим:

|АВ| = 10; |АС| = 5, следовательно =2. По формуле (2) находим координаты точки Е

х_Е = = ; у_Е = = .

Зная координаты точек А и Е находим по формуле (1) длину биссектрисы АЕ

|АЕ| = .

Ответ: |AD| = , |АЕ| = .

2. Прямая линия на плоскости. В аналитической геометрии уравнение линии в прямоугольной системе координат называется такое уравнение F(x,y)=0, которому удовлетворяют координаты всех точек, лежащих на линии, и не удовлетворяют координаты точек, не лежащих на ней.

Прямая линия на плоскости в декартовой системе координат задается линейным уравнением с двумя переменными.

Любую прямую на плоскости можно описать общим уравнением

Ах+Ву+С=0,

где А и В – координаты вектора нормали

,

перпендикулярного данной прямой (см. рис.2). Прямые, не параллельные оси ординат могут быть описаны уравнением с угловым коэффициентом k

y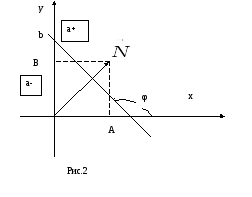=kx+b (4)

Здесь k=t gφ, где φ угол, который прямая составляет с положительным направлением оси абсцисс, отсчитываемым от оси Ох против часовой стрелки; b- ордината точки пересечения прямой с осью Оу.

Пусть заданы две прямые:

l₁: y=k₁x+b₁ ;

l₂: y=k₂x+b_2.

Тогда угол Ѳ между ними вычисляется по формуле:

Из этой формулы следует, в частности:

k₁=k₂ l₁ || l₂ (признак параллельности прямых), (5) l₁ ┴ l₂ (признак перпендикулярности прямых). (6)

Если задана точка М₀(х₀;у₀), через которую проходит прямая и известен её угловой коэффициент k, то уравнение этой прямой имеет вид:

(7)

Если же в уравнении (7) угловой коэффициент k является произвольным параметром, то это уравнение задает пучок прямых, проходящих через точку М₀(х₀;у₀).

Уравнение прямой, проходящей через две заданные точки D₀(х₀;у₀) и E₀(х₀;у₀), имеет вид:

(8)

(при условии, что и ). Если у_Е=у_D, то уравнение искомой прямой имеет вид: у=у_D. В этом случае прямая параллельна оси 0х. Если х_Е=х_D,то прямая параллельна оси 0у, и ее уравнение имеет вид: х=х_D.

Пример 2. Задан треугольник с вершинами А(1;1), В(2;5) и С(5;-1). Найти уравнение стороны ВС и средней линии МN треугольника, параллельной ВС.

Решение. Подставив координаты точек В и С в формулу (8), получаем уравнение прямой ВС:

или, окончательно,

у=-2х+9

Применяя формулу (3), найдем координаты точки N – середины стороны АВ:

Так как средняя линия параллельна стороне ВС, то k_NM= k_BC=-2 (см.(5). Подставляя известные данные в формулу (7), получаем искомое уравнение:

Ответ: 1) у=-2х+9 – уравнение прямой ВС; 2) у=-2х+6 – уравнение средней линии NM.

Пример 3. Найти проекцию точки М (8;-2) на прямую l: 3х-2у-6=0

Решение. Проекция точки М на прямую l называют точку пересечения прямой l и перпендикуляра, опущенного из точки М на l (см. рис.4). Уравнение перпендикуляра ищем в виде (4):

y+2=k(x-8)

Значение k найдем из условия перпендикулярности (6): . Для определения углового коэффициента k_l прямой l представляем её уравнение в виде у=kx+b:

O

3х-2у-6=0

Следовательно, , а , и уравнение перпендикуляра имеет вид:

или

Координаты точки N пересечения перпендикуляра и прямой l найдем, решая систему:

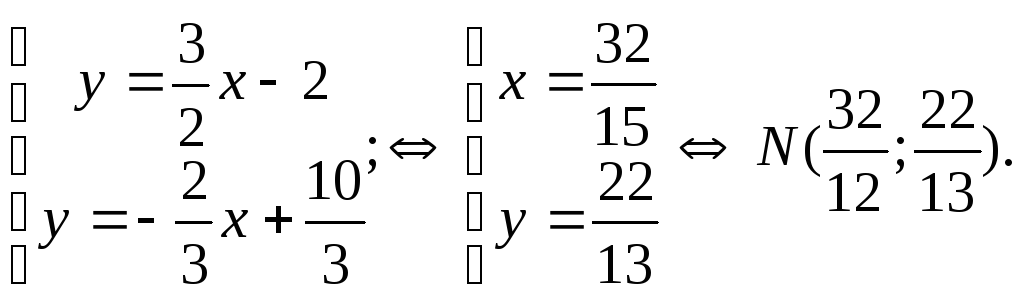
Ответ: точка является проекцией точки М на прямую l.

3. Геометрический смысл линейного неравенства с двумя неизвестными. Пусть дано уравнение

Прямая, соответствующая этому уравнению, делит плоскость х0у на две плоскости. Напомним, что данному уравнению удовлетворяют координаты только тех точек, которые лежат на этой прямой. Координаты точки М(х;у), которая лежит в одной из плоскостей (но не лежит на прямой), удовлетворяют либо неравенству Ах+Ву+С>0, либо Ах+Ву+С<0.Множество точек плоскости, координаты которых удовлетворяют неравенству Ах+Ву+С>0 (или Ах+Ву+С<0), называется областью решений соответствующего неравенства. Геометрически областью решений является полуплоскость. В случае нестрогих неравенств Ах+Ву+С ≤ 0 и Ах+Ву+С ≥ 0 в область решений, кроме полуплоскости, входит и прямая Ах+Ву+С=0.

Чтобы построить область решений неравенства, Ах+Ву+С>0 (<0) необходимо:

1. построить прямую Ах+Ву+С=0;

2. подставить в выражение Ах+Ву+С координаты любой точки, не принадлежащей прямой, и определить знак этого выражения.

Если рассматриваемое неравенство удовлетворяется, то областью решений является полуплоскость, содержащая данную точку, если же неравенство не выполнено, то областью решений служит другая полуплоскость.

Линейное неравенство можно решить графически, руководствуясь следующим правилом.

Координаты точек той плоскости, которая расположена от прямой Ах+Ву+С=0 в направлении вектора нормали , удовлетворяют неравенству Ах+Ву+С>0. Обозначим эту полуплоскость а⁺ (см.рис.2).

Координаты точек полуплоскости, которая расположена от прямой Ах+Ву+С=0 в направлении, противоположном направлению вектора нормали , удовлетворяют неравенству Ах+Ву+С<0. Обозначим эту полуплоскость а^- (см.рис.2).

Пример 4. Дана прямая 2х-5у+6=0 и точки М(-2,2) и К (5;1). Выяснить, лежат ли эти точки по одну или по разные стороны от данной прямой.

Решение. Прямая 2х-5у+6=0 делит плоскость на две полуплоскости

2х-5у+6>0 и 2х-5у+6<0.

Подставим координаты точек М и К в выражение 2х-5у+6. Координаты точки удовлетворяют неравенству 2х-5у+6<0:

2·(-2)-5·2+6=-8<0

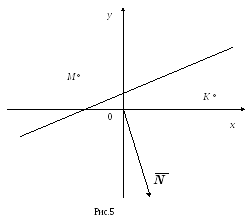
Значит, точка М предлежит плоскости а^-. Аналогично, для точки К имеем: 2·5-5·1+6=11>0.

Значит, точка К принадлежит полуплоскости а⁺, определяемой неравенством 2х-5у+6>0. Следовательно, заданные точки М и К лежат в разных полуплоскостях, т.е. по разные стороны прямой 2х-5у+6=0.

Ответ: точки М и К лежат по разные стороны от данной прямой.

4. Элементы векторной алгебры. Векторы принято обозначать либо , либо , где А –начало, а В – конец вектора. В выбранной системе координат вектор однозначно задается своими координатами:

, (на плоскости),

(9)

, (в пространстве),

где а_х.,а_у.,а_z- координаты вектора, а - единичные векторы сонаправленные с координатными осями (орты координатных осей). Равенства (9) называются разложением вектора по координатным осям.

Координаты вектора = связаны с координатами его концов А(х_А;,у_А;z_A) и В (х_В,;у_В; z_В) формулами:

а_х=х_В-х_А, а_у=у_В-у_А, а_z=z_В-z_А (10)

Скалярным произведением двух векторов называют произведение их длин на косинус угла φ между этими векторами

Для векторов, заданных в координатной форме, справедливы соотношения:

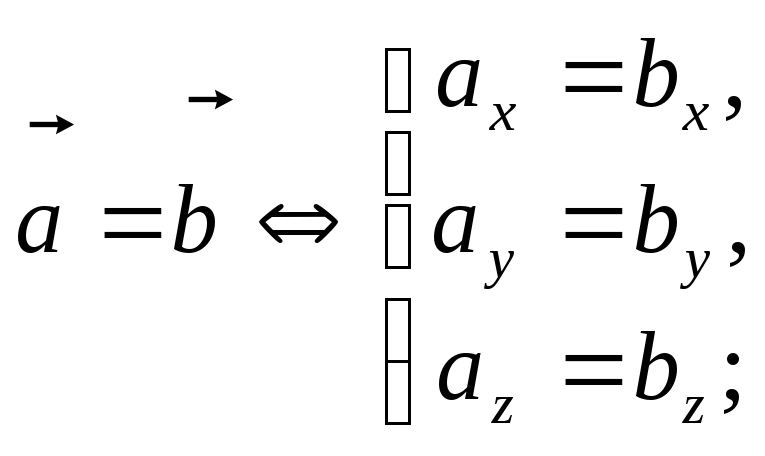
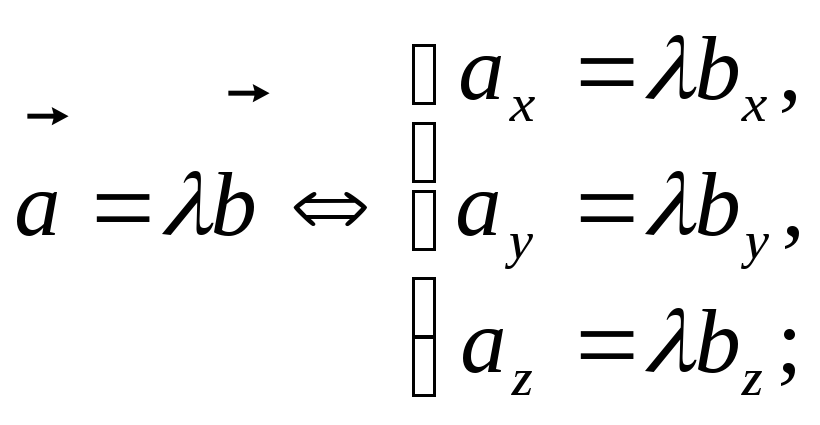(11)

;

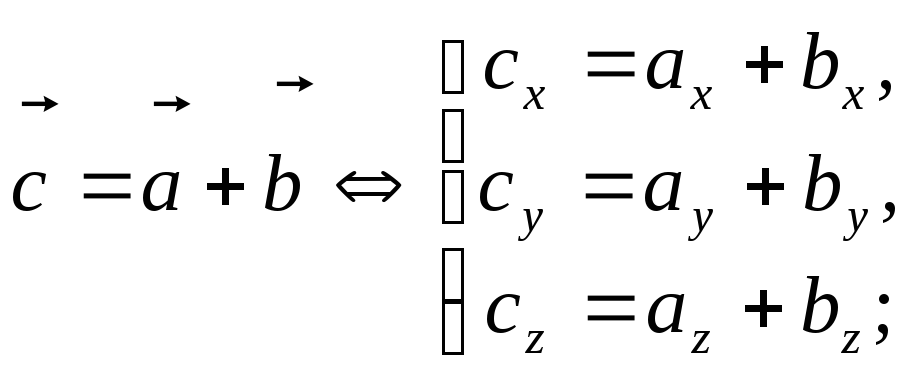
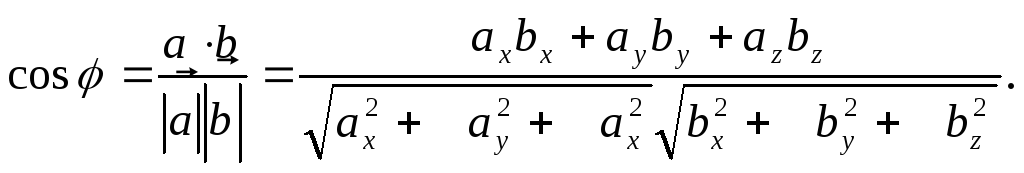(12)

Пример 5. Найти вектор и косинус угла между векторами и , если известно, что = , = , где A (1;-3;2), В (4;5;-1), С(0;2;-3), D (3;-2;5) – заданные точки.

Решение: Найдем координаты векторов и по формуле (10):

a_x=4-1=3, а_у=5+3=8, а_z=-1-1=-3;

Аналогично, . Вектор и cosφ найдем по формулам (11) и (12).

Ответ: 1) 2)