8. Нахождения наибольшего и наименьшего значений непрерывной функции на отрезке

Алгоритм нахождения наибольшего и наименьшего значений непрерывной функции на отрезке:

1) Найти все критические точки функции, принадлежащие отрезку ;

2) Вычислить значения функции в этих точках и на концах отрезка;

3) Из полученных значений выбрать наибольшее и наименьшее.

Пример 8.1. Найти наибольшее и наименьшее значения функции на отрезке .

Решение. 1) Найдем критические точки функции.

,  

 .

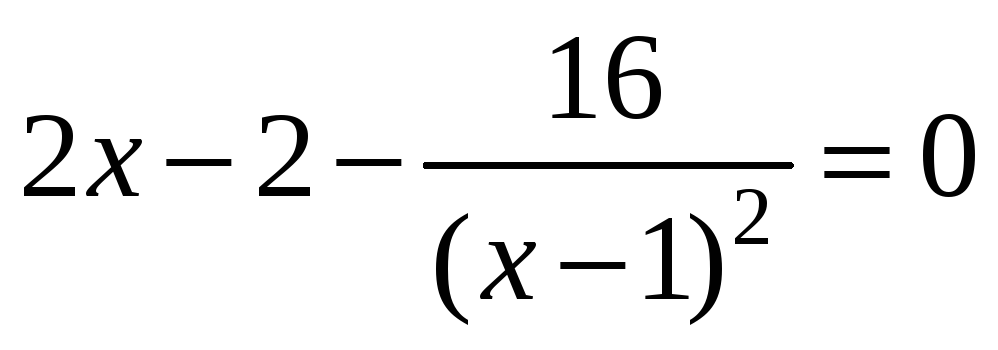
На отрезке знаменатель не обращается в нуль. Следовательно, дробь равна нулю тогда и только тогда, когда числитель равен нулю:

   .

Значит, – критическая точка функции. Она принадлежит данному отрезку.

Найдем значение функции в критической точке:

.

2) Найдем значения функции на концах отрезка:

, .

3) Из полученных значений выбираем наибольшее и наименьшее:

, .

9. Задачи на отыскание наибольших и наименьших значений величин

При решении задач на вычисление наименьших и наибольших значений величин надо прежде всего определить, для какой величины в задаче требуется найти наименьшее или наибольшее значение. Эта величина и будет исследуемой функцией. Затем одну из величин, от изменения которых зависит применение функции, следует взять за независимую переменную и выразить через неё функцию. При этом нужно в качестве независимой переменной выбрать ту величину, через которую исследуемая функция выражается проще всего. После этого решается задача на нахождение наименьшего и наибольшего значения полученной функции в некотором промежутке изменения независимой переменной, которое обычно устанавливается из самого существа задачи.

Пример 9.1. Найти высоту конуса наибольшего объёма, который можно вписать в шар радиуса .

Решение. Обозначив радиус основания, высоту и объём конуса соответственно , и , запишем . Это равенство выражает зависимость от двух переменных и ; исключим одну из этих величин, а именно . Для этого из прямоугольного треугольника выводим (по теореме о квадрате перпендикуляра, опущенного из вершины прямого угла на гипотенузу):

Рисунок 6 – Иллюстрация к примеру 9.1.

или .

Подставив значение в формулу объёма конуса, получим:

.

Мы видим, что объём конуса, вписанного в шар радиуса ,есть функция от высоты этого конуса . Найти высоту при которой вписанный конус имеет большой объём, это значит найти такое , при котором функция имеет максимум. Ищем максимум функции:

1) ,

2) , , , откуда или ,

3) .

Подставив вместо сначала , а потом , получим:

В первом случае имеем минимум ( при ), во втором искомый максимум (так как при ).

Следовательно, при конус, вписанный в шар радиуса , имеет наибольший объём.

П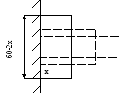ример 9.2. Требуется огородить проволочной сеткой длиной 60 м прямоугольный участок, прилегающий к стене дома (рис. 7). Каковы должны быть длина и ширина участка, чтобы он имел наибольшую площадь?

Решение. Пусть ширина участка м, а площадь м², тогда:

Рисунок 7 – Иллюстрация к пр. 9.2.

.

Значения и не могут быть отрицательными, поэтому множитель , а .

Площадь есть функция , определим промежутки ее возрастания и убывания:

. , и функция возрастает, когда ; , и функция убывает, когда . Следовательно, точка является точкой максимума. Так как это единственная точка, принадлежащая интервалу , то в точке функция имеет наибольшее значение.

Следовательно, площадь участка наибольшая (максимум), если ширина м, а длина м.

Пример 9.3. Каковы должны быть размеры прямоугольной комнаты, площадь которой 36 м², чтобы периметр ее был наименьший?

Решение. Пусть длина равна м, тогда ширина прямоугольника м, а периметр:

.

Периметр есть функция длины , определенная для всех положительных значений : .

Определим промежутки ее возрастания и убывания:

.

Знак производной определяется знаком разности . В промежутке

, а в промежутке .

Следовательно, точка является точкой минимума. Так как это единственная точка, принадлежащая интервалу: , то в точке функция имеет наименьшее значение.

Следовательно, периметр прямоугольника имеет наименьшее значение (минимум), если длина его 6 м и ширина м = 6 м, т. е. когда он квадрат.