
- •Определители n-го порядка.
- •Обратная матрица.
- •Система n линейных уравнений с n неизвестными.
- •Произвольная система линейных уравнений.
- •Линейные операции над векторами в координатной форме.
- •Линейное пространство
- •Размерность и базис линейного пространства
- •Скалярное произведение векторов
- •Скалярное произведение в координатной форме
- •Векторное произведение векторов.
- •Векторное произведение в координатной форме
- •Смешанное произведение векторов.
- •Аналитическая геометрия Простейшие задачи аналитической геометрии
- •Полярная система координат
- •Формулы преобразования системы координат
- •1. Параллельный перенос
- •Поворот осей координат
- •Уравнение прямой на плоскости
- •Нормальное уравнение прямой
- •Расстояние от точки до прямой
- •Нормальное уравнение прямой
- •Расстояние от точки до плоскости
- •Угол между двумя прямыми в пространстве
- •Асимптоты гиперболы
- •Эксцентриситет гиперболы, фокальные радиусы гиперболы
- •Парабола
- •Общие свойства кривых второго порядка
- •Приведение общего уравнения второго порядка к каноническому виду
Угол между двумя прямыми в пространстве
Даны 2 прямые в пространстве, заданные каноническими уравнениями прямых в пространстве, следовательно, известны их направляющие векторы;
![]()

За угол между двумя прямыми в пространстве принимается угол между их направляющими векторами:
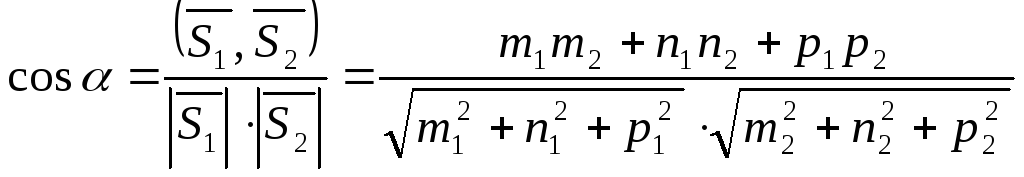
Условие
параллельности:
так как прямые параллельны, их направляющие
векторы коллинеарны, следовательно,
![]() - условие параллельности прямых;
- условие параллельности прямых;
Условие
перпендикулярности:
если прямые перпендикулярны, то их
направляющие векторы тоже перпендикулярны,
следовательно,
![]() - условие перпендикулярности прямых в
пространстве
- условие перпендикулярности прямых в
пространстве
Угол между прямой и плоскостью
Д ано:
плоскость P,
ано:
плоскость P,
![]()
![]()
![]() под
под
![]()
![]() - направляющий
вектор прямой;
- направляющий
вектор прямой;
![]() – угол между
– угол между
![]() и
и
![]()
![]()
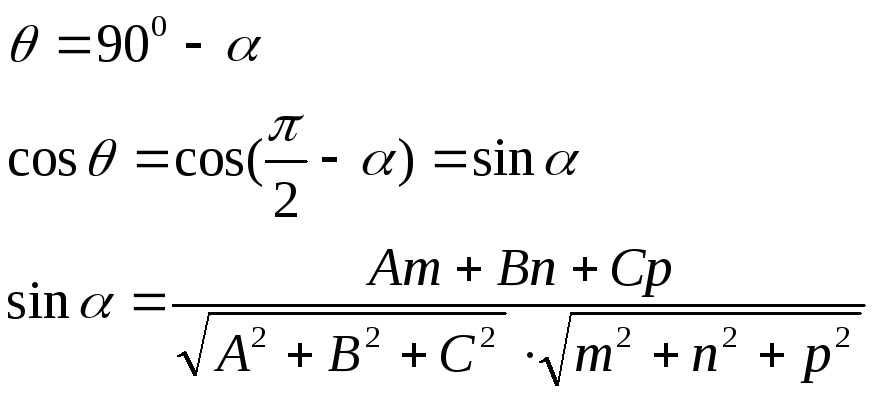
Условие
параллельности прямой и плоскости:
![]() ,
т.е.
,
т.е.
![]()
Условие
перпендикулярности прямой и плоскости:
![]() ,
т.е.
,
т.е.
![]()
Угол между двумя плоскостями
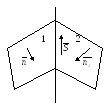
Дано: Р1 и Р2 – две плоскости;
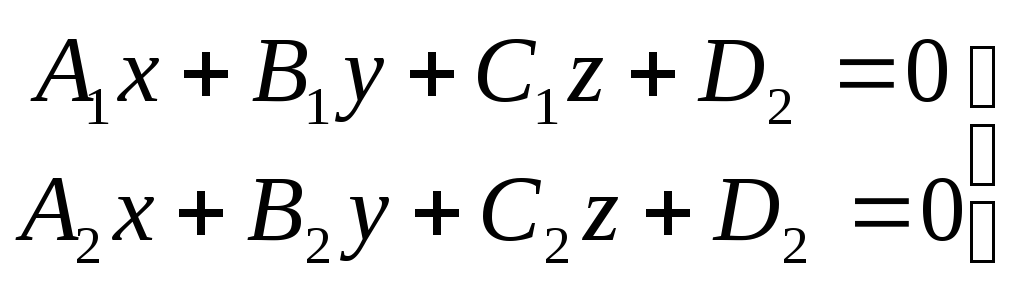
![]() - нормальный вектор
плоскости Р1
- нормальный вектор
плоскости Р1
![]() - нормальный вектор
плоскости Р2
- нормальный вектор
плоскости Р2
Две плоскости,
пересекаясь, образуют 4 двухгранных
угла, равных попарно. Один из них равен
углу между нормальными векторами.
Обозначая один из этих углов через
![]() ,
имеем:
,
имеем:
![]()
Выбирая знак «+»,
получаем
![]() ,
выбирая знак « -
«, получаем
,
выбирая знак « -
«, получаем
![]()
Условие параллельности 2-х плоскостей
Если плоскости параллельны, то их нормальные векторы коллинеарны:
![]() ,
следовательно, их координаты
пропорциональны:
,
следовательно, их координаты
пропорциональны:
![]()
Условие перпендикулярности 2-х плоскостей
Если плоскости перпендикулярны, то их нормальные векторы перпендикулярны:
![]() ,
следовательно,
,
следовательно,
![]()
Кривые второго порядка
Алгебраические уравнения второй степени относительно декартовой системы координат вида Ах2+2Вху+Су2+Dх+Еу+F=0 представляют собой кривые второго порядка: окружность, эллипс, гипербола, парабола.
Эллипс
Опр.: Эллипс - геометрическое место точек на плоскости, сумма расстояний от которых до 2 данных точек (называемых фокусами) есть величина постоянная и равна 2а.
y
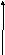




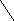 y M(x,y)
y M(x,y)
r2 r1
F2(-c,0) 0 x F1(c,0) x
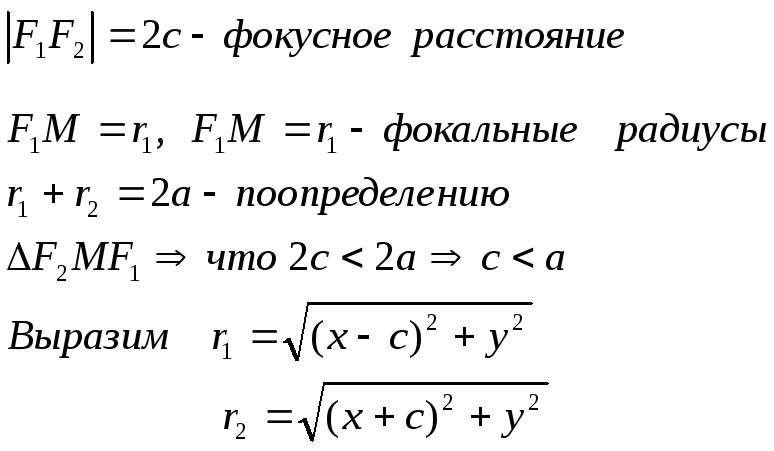
![]()
![]()

Исследование формы эллипса
т.к. х и у входят в уравнение в четных степенях, то график симметричен относительно осей координат.
.
![]()
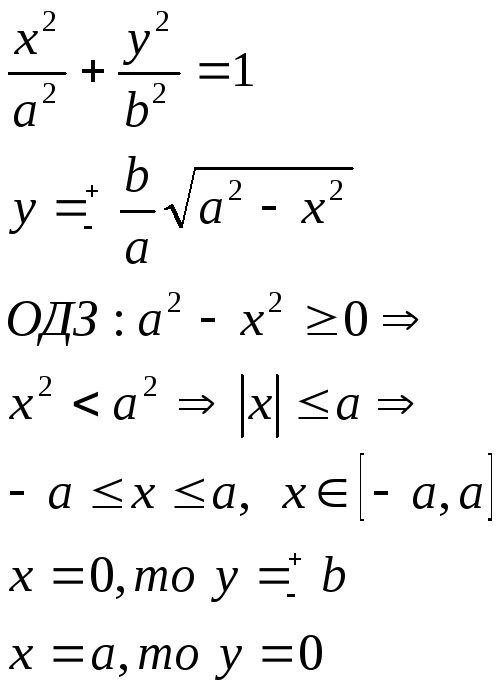
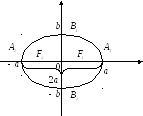
A1,A2,B1,B2 – вершины эллипса;
A1A2=2a – большая ось эллипса, a - большая полуось;
В1В2=2b – малая ось, b – малая полуось;
![]() - фокусное
расстояние.
- фокусное
расстояние.
Эксцентриситет эллипса и его влияние на форму
Опр.:
Эксцентриситет-
отношение фокусного расстояния к большой
оси
![]() .
.
![]() =
=![]()
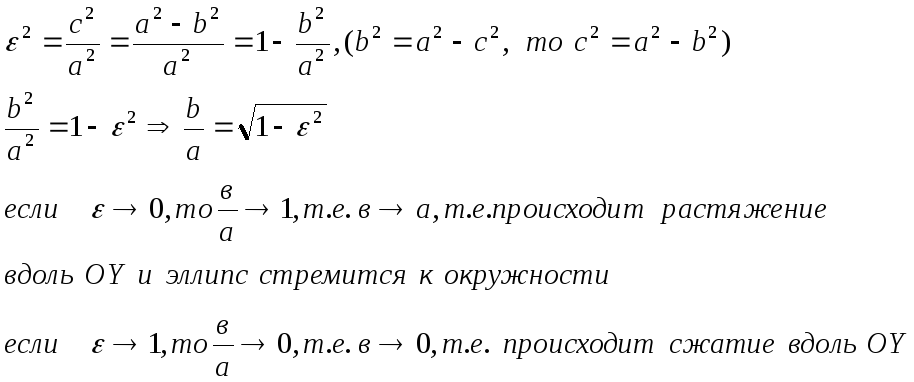
Директриса эллипса и фокальный радиус
Директриса эллипса
– это прямые, перпендикулярные большой
оси эллипса и отстающие от центра на
расстояние
![]()
т.к.
![]() <1,
то
<1,
то
![]() ,
расстояние между директрисами
,
расстояние между директрисами
![]() ;
;
уравнение директрис
![]()
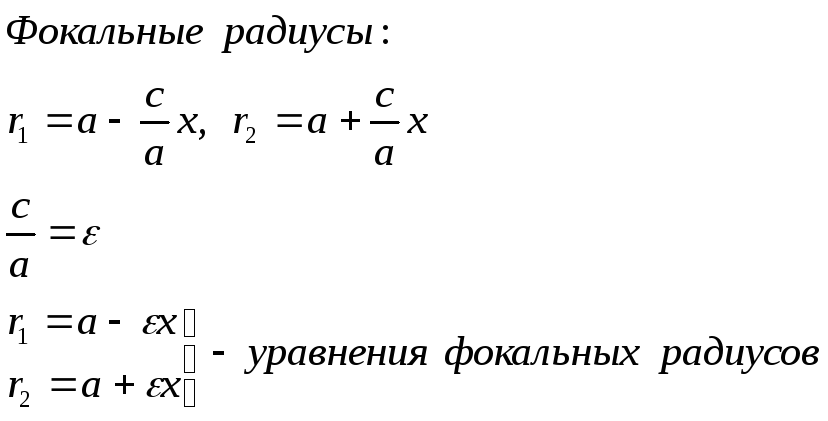



![]() -а а
-а а
![]()
![]()
Гипербола
Опр.: Гипербола – геометрическое место точек на плоскости, для каждой из которых модуль разности расстояний до 2 данных точек, называемых фокусами, есть величина постоянная и равна 2a.
у
М(х,у)
r2 r1


F2(-c,0) F1(c,0) х


Исследование формы гиперболы
Т.к. х и у входят в уравнение в четных степенях, то график симметричен относительно координатных осей.
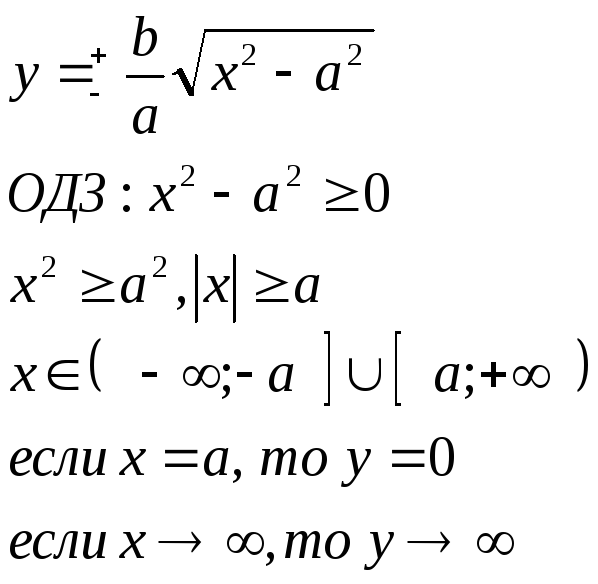
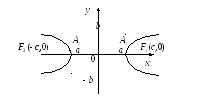
A1, A2 – вершины гиперболы
2а – действительная ось гиперболы
а – действительная полуось
2b – мнимая ось гиперболы
b – мнимая полуось
