Нормальное уравнение прямой

Дано: плоскость Р,, p – расстояние от 0 до P, n – единичный вектор

Возьмем точку

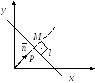
- радиус вектор

- нормальное уравнение плоскости в векторной форме

Запишем в координатной форме:

,

- нормальное уравнение плоскости в координатной форме;

Приведение общего уравнения плоскости к нормальному виду:

Умножим первое уравнение на μ (нормирующий множитель) так, чтобы уравнение стало нормальным, то есть

Возведем обе части 3-х предыдущих равенств в квадрат и сложим, получим

- формула для вычисления нормирующего множителя

, так как μ и D имеют противоположные знаки, следовательно множитель μ противоположен знаку D.

Лекция 7

Расстояние от точки до плоскости

Дано: плоскость Р задана нормальным уравнением в векторной форме , Требуется найти расстояние от точки до плоскости;

Возможны 2 случая:

3. т. М₀ и начало координат лежат по разные стороны от плоскости

4. т. М₀ и начало координат лежат по одну сторону от плоскости

Рассмотрим 1 случай.

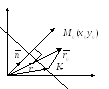соединим и 0 - радиус вектор точки М₀

Опустим из точки перпендикуляр на P, обозначим точкой K(x,y,z)

- расстояние от точки до плоскости. Соединим точку О с точкой K, получим - радиус-вектор точки К.

Из треугольника ОМ₀К видно, что

с одной стороны, а с другой стороны

, а так как точка К принадлежит P, значит, координаты ее радиус вектора координаты удовлетворяют уравнению в векторной форме; подставляем и получаем по свойству скалярного произведения , отсюда - расстояние от точки до плоскости;

Во втором случае - общий случай

Найдем расстояние от точки до плоскости в координатной форме:

- расстояние от точки до прямой в координатной форме.

- отклонение точки от прямой

Если Δ>0, то и 0 лежат по разные стороны от плоскости;

Если Δ<0, то по одну сторону от плоскости;

Вывод.: чтобы найти расстояние от точки до плоскости, нужно уравнение привести к нормальному виду и подставить вместо х и у координаты заданной точки.

Прямая в пространстве

Каноническое и параметрическое уравнения прямых в пространстве

Дано: прямая l, т. - направляющий вектор прямой l,

Возьмем произвольную т. M на прямой и рассмотрим - каноническое уравнение прямой.

, t – параметр,

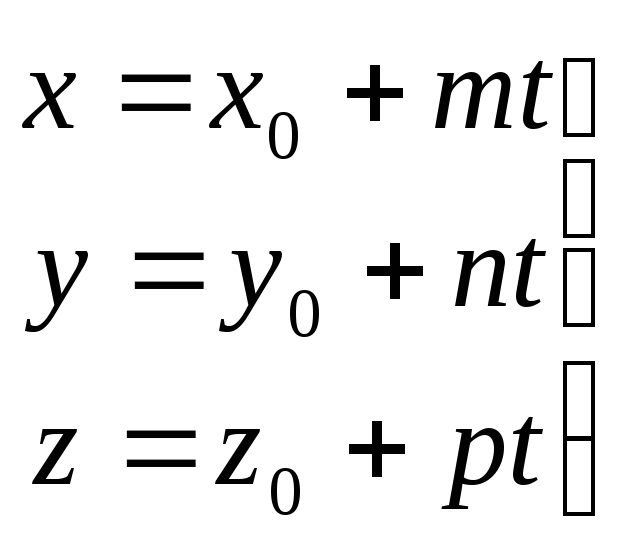- параметрическое уравнение прямой.

Уравнение прямой, проходящей через 2 точки

Дано: и

Используем каноническое уравнение прямой:;

В качестве направляющего вектора прямой используем вектор , так как он лежит на прямой.

- уравнение прямой, проходящей через две заданные точки.

О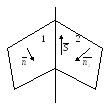бщее уравнение прямой

Даны две пересекающиеся плоскости, заданные общим уравнением:

(*)

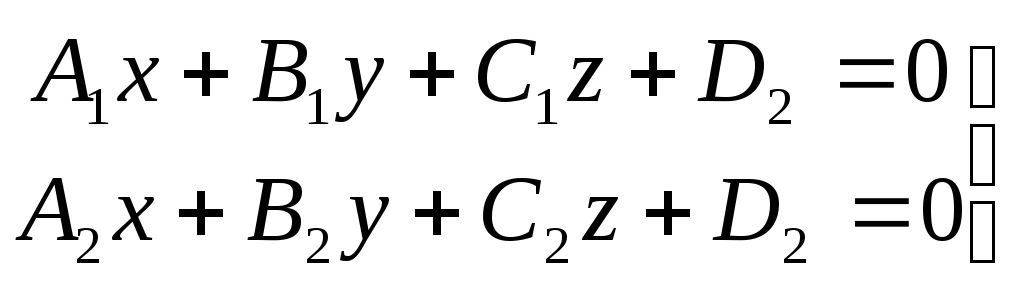Так как они пересекаются, их нормальные векторы не коллинеарны. Линия пересечения – прямая, следовательно, система двух уравнений (*) называется общим уравнением прямой в пространстве.

Приведение общего уравнения к каноническому виду

- канонический вид;

- направляющий вектор

- нормальный вектор плоскости Р₁

- нормальный вектор плоскости Р₂

В качестве направляющего вектора прямой возьмем ;

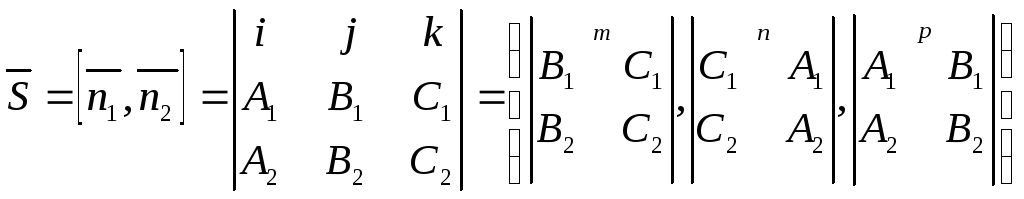
В качестве точки используем частное решение системы (*), так как система имеет бесконечное множество решений (ранг меньше количества неизвестных).

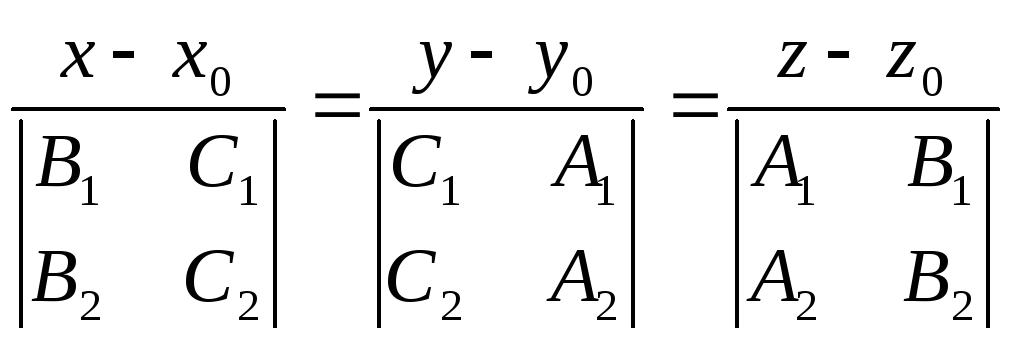- канонический вид уравнения

Уравнение пучка плоскостей

Совокупность плоскостей, проходящих через одну и туже прямую, называется пучком плоскостей.

Даны две пересекающиеся плоскости:

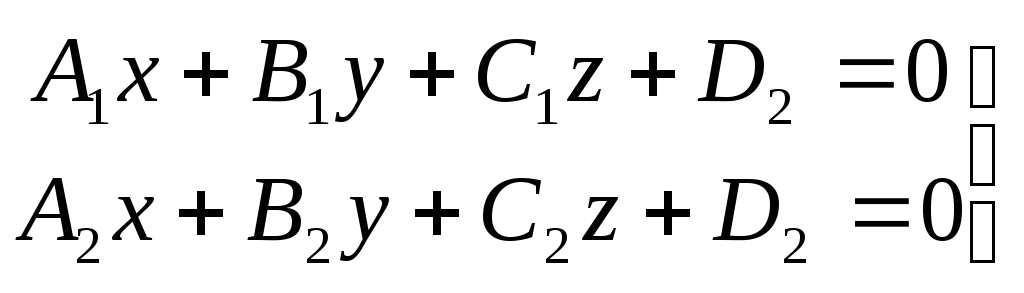
Пересечение – прямая l;

Умножим второе уравнение на и сложим с первым уравнением;

(*)

Покажем, что это уравнение определяет плоскость; для этого возьмем т. , принадлежащую линии пересечения двух плоскостей и покажем что (*) проходит через прямую ;

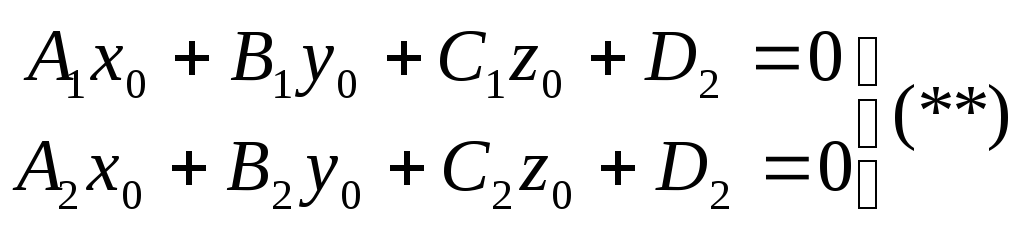
(см. (**)), следовательно, - уравнение пучка плоскостей в пространстве.

Совокупность прямых в пространстве, проходящих через одну точку, называется связкой.