
- •Определители n-го порядка.
- •Обратная матрица.
- •Система n линейных уравнений с n неизвестными.
- •Произвольная система линейных уравнений.
- •Линейные операции над векторами в координатной форме.
- •Линейное пространство
- •Размерность и базис линейного пространства
- •Скалярное произведение векторов
- •Скалярное произведение в координатной форме
- •Векторное произведение векторов.
- •Векторное произведение в координатной форме
- •Смешанное произведение векторов.
- •Аналитическая геометрия Простейшие задачи аналитической геометрии
- •Полярная система координат
- •Формулы преобразования системы координат
- •1. Параллельный перенос
- •Поворот осей координат
- •Уравнение прямой на плоскости
- •Нормальное уравнение прямой
- •Расстояние от точки до прямой
- •Нормальное уравнение прямой
- •Расстояние от точки до плоскости
- •Угол между двумя прямыми в пространстве
- •Асимптоты гиперболы
- •Эксцентриситет гиперболы, фокальные радиусы гиперболы
- •Парабола
- •Общие свойства кривых второго порядка
- •Приведение общего уравнения второго порядка к каноническому виду
Аналитическая геометрия Простейшие задачи аналитической геометрии
Линейная алгебра исследует СЛУ, т.е. уравнения, содержащие неизвестные в первой степени. Аналитическая геометрия – раздел математики, в которой изучаются геометрические объекты с помощью алгебраических методов. Основной метод – метод координат.
-
Расстояние между 2-мя точками.
Заданы две точки:
![]()
![]()
Расстояние между двумя точками.
-
Деление отрезка в данном отношении.
![]()
Требуется найти
т.
![]() ,
которая делит отрезок в данном отношении
,
которая делит отрезок в данном отношении
![]() .
.
Рассмотрим 2 вектора
![]() и
и
![]() ,
следовательно,
,
следовательно,
![]()
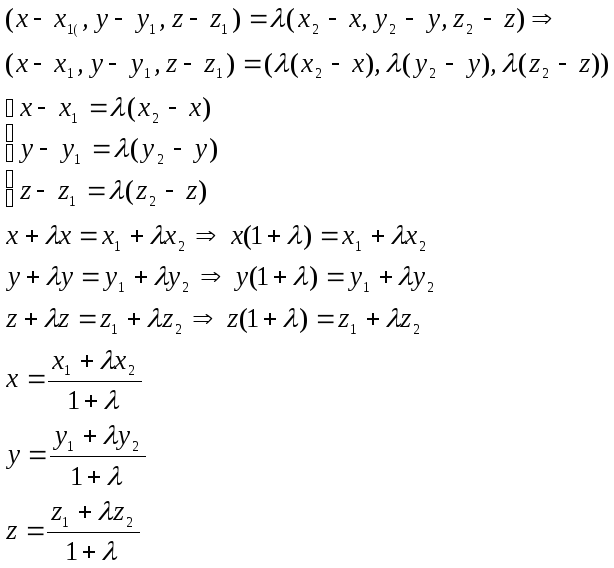
Полярная система координат
Полярная система координат на плоскости задается точкой О – полюсом, лучом ОР – полярной осью и единицей масштаба. Будем считать положительным поворотом вокруг т. О - поворот против часовой стрелки.
Рассмотрим
произвольную т. М;
![]() - полярный радиус; угол на который надо
повернуть луч ОР,
чтобы он
совпал с ОМ,
обозначим через
- полярный радиус; угол на который надо
повернуть луч ОР,
чтобы он
совпал с ОМ,
обозначим через
![]() и назовем полярным углом.
и назовем полярным углом.
Полярными
координатами т. М называются ее полярный
радиус
![]() и полярный угол
и полярный угол
![]() .
.
Наряду с введенной полярной системой координат рассмотрим прямоугольную декардову систему координат такую, чтобы полюс совпадал с началом координат, а полярная ось – с положительной полуосью ОХ.
Тогда, если М(х,у)
– декардовы координаты, а М(![]() )
– полярные координаты, то
)
– полярные координаты, то
![]() - выражение
декардовых координат через полярные
координаты;
- выражение
декардовых координат через полярные
координаты;
![]() - выражение полярных
координат через декардовы координаты.
- выражение полярных
координат через декардовы координаты.
Пример:
Рассмотрим уравнение
окружности:
![]()
![]()
- уравнение окружности в полярной системе координат.
Формулы преобразования системы координат
1. Параллельный перенос
Рассмотрим декардову прямоугольную систему координат и в ней т. М(х,у);
Перенесем начало координат в т. О(a,b); тогда координаты т.М в новой системе координат будут M(x’,y’), и тогда x=x'+a, y=y’+b – формулы перехода от новых координат к старым; x'=x-a, y'=y-b – формулы перехода от новых координат к старым.

-
Поворот осей координат
![]()
![]()
![]() - формулы поворота осей координат.
- формулы поворота осей координат.
![]()
Уравнение прямой на плоскости
Линии определены
уравнением Ax+By+С=0,
где
![]() являются прямыми.
являются прямыми.
Дано прямая l,![]()
Н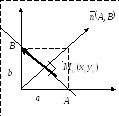 аписать
уравнение прямой.
аписать
уравнение прямой.
В![]()
![]() озьмём
точку на l
– произвольная точка и рассмотрим
вектор
озьмём
точку на l
– произвольная точка и рассмотрим
вектор
![]()
![]()
![]()
![]()
![]() - уравнение прямой, проходящей через
данную точку. Раскроем скобки:
- уравнение прямой, проходящей через
данную точку. Раскроем скобки:
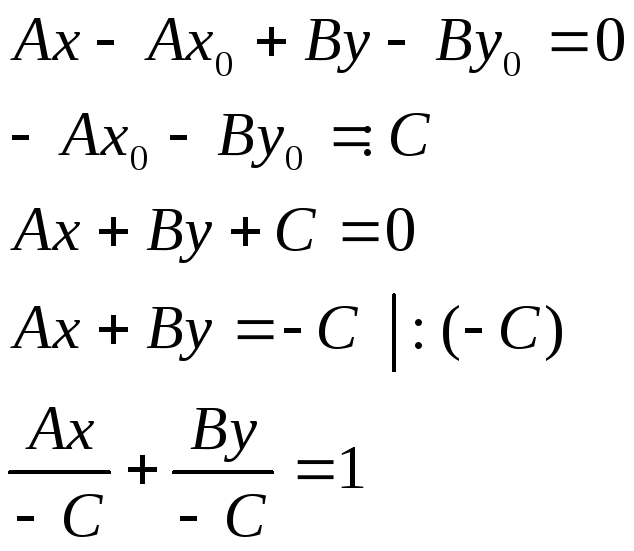 -
общее уравнение прямой
-
общее уравнение прямой
![]()
![]() - уравнение прямой
в отрезках
- уравнение прямой
в отрезках
Нормальное уравнение прямой
Дано: прямая l
,![]() ,
p
– расстояние от 0 до l,
n
– единичный вектор
,
p
– расстояние от 0 до l,
n
– единичный вектор
Возьмем точку
![]()
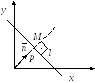
![]() - радиус вектор
- радиус вектор
![]()
![]()
![]()
![]() - нормальное
уравнение прямой в векторной форме
- нормальное
уравнение прямой в векторной форме
Запишем в координатной форме:
![]() ,
,
![]()
то вектор имеет
координаты
![]()
![]() - нормальное
уравнение прямой в координатной форме;
- нормальное
уравнение прямой в координатной форме;
Приведение общего уравнения прямой к нормальному виду:
![]()
![]()
Умножим первое
уравнение на μ
(нормирующий множитель) так, чтобы
уравнение стало нормальным, то есть
![]()
![]()
![]()
Возведем обе части 2-х предыдущих равенств в квадрат и сложим, получим
![]()
![]() - формула для
вычисления нормирующего множителя
- формула для
вычисления нормирующего множителя
![]() ,
так как μ
и С имеют противоположные знаки,
следовательно множитель μ
противоположен знаку С.
,
так как μ
и С имеют противоположные знаки,
следовательно множитель μ
противоположен знаку С.
Лекция 7
