Линейные операции над векторами в координатной форме.

Даны 2 вектора:

Условие коллинеарности векторов в координатной форме:

Так как вектора коллинеарные, то =, тогда

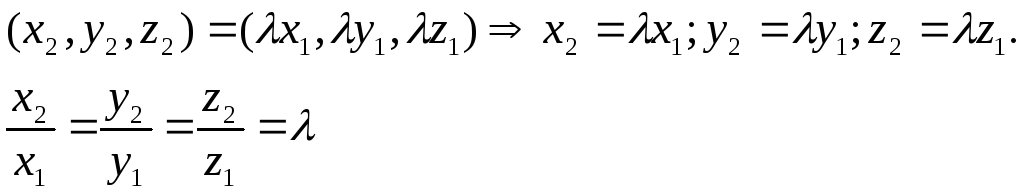
Следовательно, - условие коллинеарности векторов в координатной форме.

Лекция 5

n-мерный вектор. Линейная зависимость и независимость векторов.

Опр.: n-мерным вектором называется упорядоченный набор из n вещественных чисел а=(х₁,х₂…х_п), где х₁,х₂…х_п- координаты вектора.

Действия:

1. 2 вектора равны, если равны их соответствующие координаты.

2. =

3.

4.Дана система из m n-мерных векторов: Вектор , где - скаляры, называют линейной комбинацией векторов

Опр.(*) Система векторов называется линейно зависимой, если какой-либо из этих векторов может быть представлен в виде линейной комбинации остальных векторов. В противном случае система называется линейно независимой.

Опр. (**) Система векторов называется линейно зависимой, если существуют скаляры такие, что соотношение выполняется хотя бы при одном . Если же это соотношение выполняется только лишь в случае , то система называется линейно независимой.

Замечание: система из одного ненулевого вектора – линейно независимая, так как тогда и только тогда, когда .

Система из одного вектора линейно зависимо, тогда и только тогда, когда

Теорема:

Определения (*) и (**) равносильны.

Пусть система векторов линейно зависима в смысле определения (*), тогда какой-либо вектор этой системы можно представить в виде линейной комбинации остальных векторов. Для определенности положим , следовательно, , следовательно, , т.е. система линейно зависима всмысле определения (**).

Обратно: пусть система линейно зависима в смысле определения (**), тогда выполняется хотя бы при одном . Для определенности положим, что , тогда , следовательно, , где - скаляры. Следовательно, представлен в виде линейной комбинации остальных векторов, следовательно, система линейно зависима в смысле определения (*).

Линейное пространство

Рассмотрим множество и множество R действительных чисел.

Введем в V операцию сложения и умножения элементов множества V на действительные числа:

1. x+y=z, x,y,zV

2. x∙α=z, хV, α R, zV.

Также потребуем, чтобы операция сложения и умножения на число удовлетворяли следующим аксиомам:

1. x+y=y+x

2. (x+y)+z=x+(y+z)

3. Существует нулевой элемент, который в сумме с любым элементом дает тот же элемент

4. Существует противоположный элемент: x+(-x)=0, x

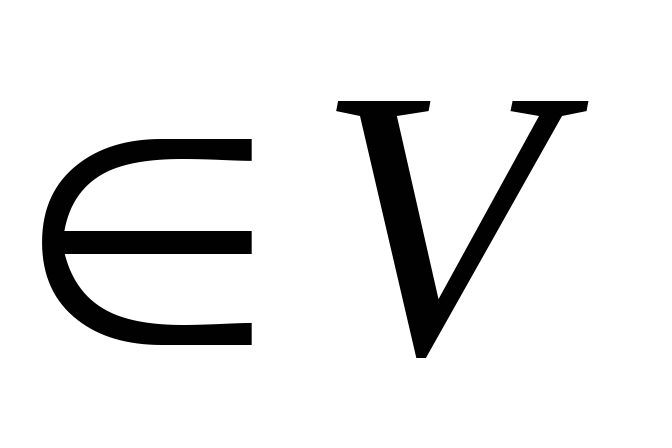
5. 1∙x=x, x

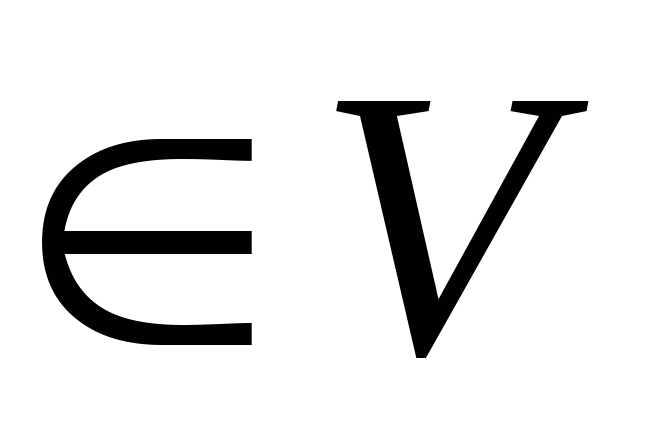
6. α(β∙x)=(α∙β)x, α,β

7. 

8. 

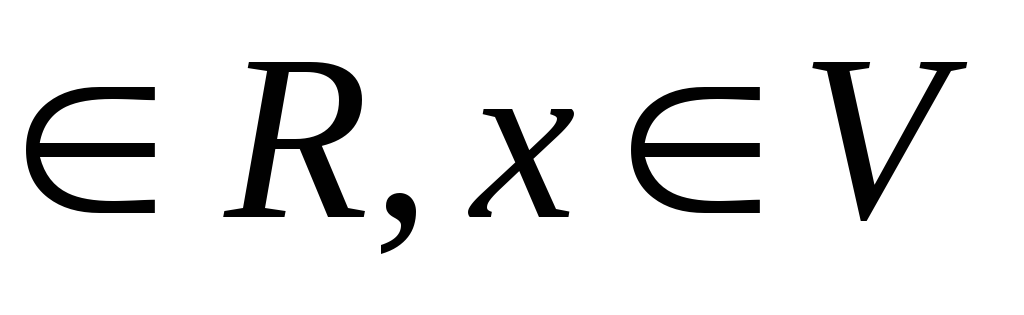
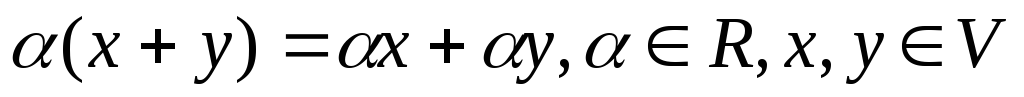
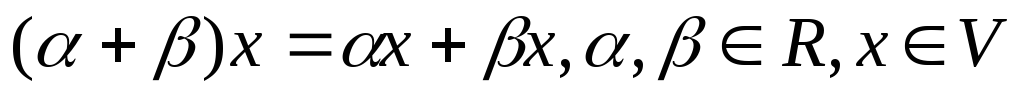
В случае, когда заданы операция сложения и умножения на число и выполнены 8 аксиом, говорят, что задано линейное пространство (V)

Примеры:

1. Множество векторов 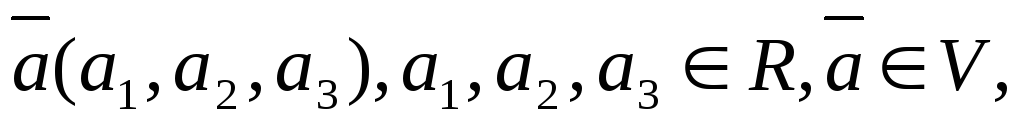в этом случае множество векторов являющихся линейным пространством

2. Множество всех матриц размерностью 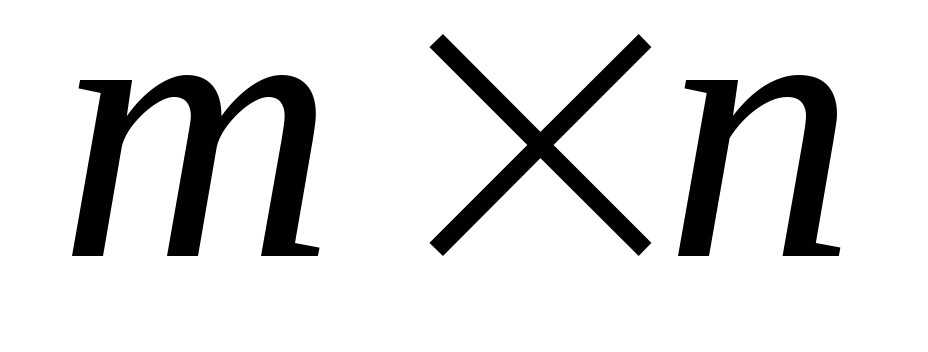- линейное пространство

Размерность и базис линейного пространства

Линейное пространство - n-мерное, если в нем существует система из n-линейно независимых векторов, а любая система из (n+1) векторов является линейно зависимой, таким образом размерность линейного пространства - это наибольшее количество линейно независимых элементов в нем.

Базисом n-мерного линейного пространства является любая упорядоченная систем n-мерного независимых векторов в нем.

Напр.: базис - образуют тройка некомпланарных векторов.

Опр.: Вектора некомпланарные, если они не лежат в одной плоскости.

Иными словами множество из n- векторов называется базисом, если оно линейно независимо и любой вектор этого пространства можно представить как линейную комбинацию базисных векторов.

Th1: Система из n-единичных векторов в пространстве образует базис

Th2: Любой вектор пространства может быть представлено в виде линейной комбинации базисных векторов единственным образом.

Пр.: Образует ли в любом пространстве - базис?

по базису

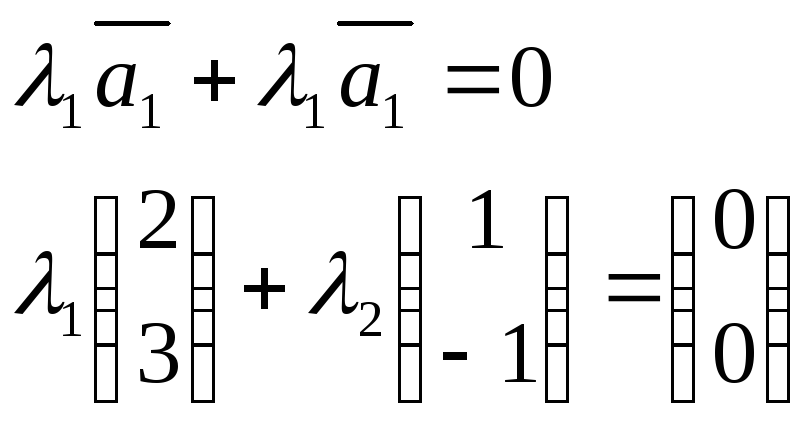
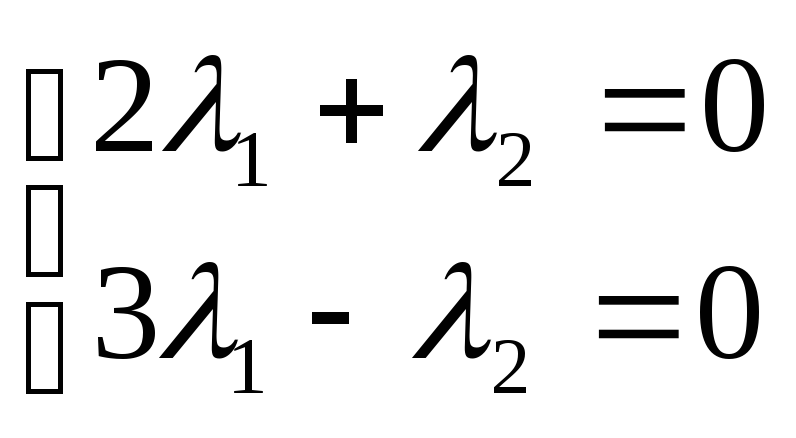
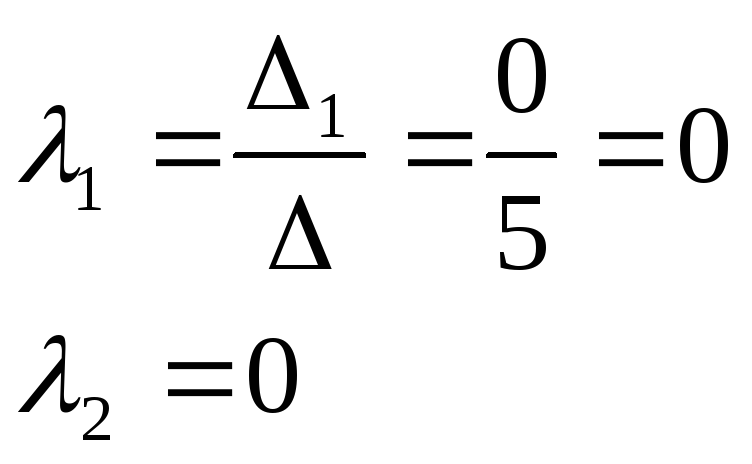
и - линейно независимы

и базис в

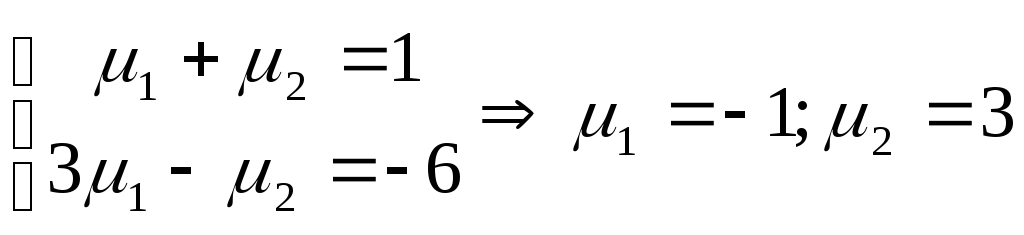- координаты