
- •Теория функций комплексного переменного §1. Действия с комплексными числами
- •§2. Функция комплексной переменной
- •§ 3. Дифференцирование функции комплексной переменной
- •§4. Интеграл в комплексной плоскости
- •§5 Ряды тейлора и лорана, вычеты
- •Функциональный анализ §6 линейные пространства
- •§7 Ряды фурье
- •§8 Интеграл лебега
- •Задачи повышенной сложности
- •Список рекомендованной литературы
§5 Ряды тейлора и лорана, вычеты
Функция f(z),
аналитическая в круге |z-z0
|<R,
однозначно представляется в нём рядом
Тейлора
![]() ,
где
,
где
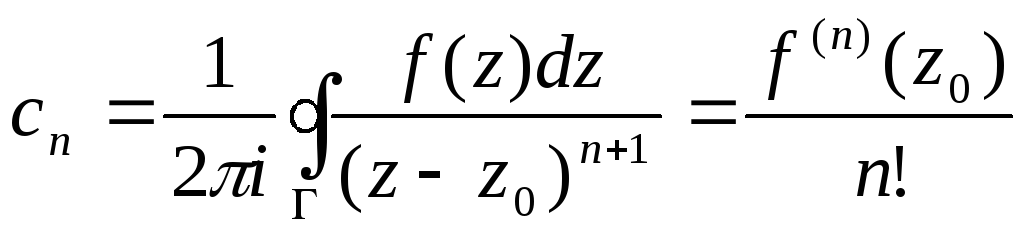 .
.
Разложение основных элементарных функций в ряд Тейлора при z0=0 имеет вид
![]()
![]()
![]()
![]() /
/
Если f(z)
аналитическая
в кольце r<|z-z0|<R
,то для неё
существует ряд Лорана
![]() ,
где
,
где
![]() .
.
Вычетом аналитической
функции f(z)
в изолированной
особой точке z0
называется
комплексное число, равное
![]() ,
т.е. коэффициенту c-1
ряда
Лорана.
,
т.е. коэффициенту c-1
ряда
Лорана.
Если z0
–полюс первого порядка функции
![]() ,
то
,
то
![]() .
.
Если z0
–полюс m-го
порядка функции f(z),
то
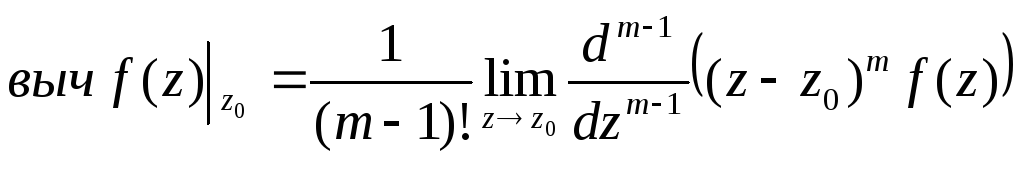 .
.
Теорема о вычетах.
Если f(z)
аналитическая
функция в замкнутой области D
за исключением конечного числа
изолированных особых точек
![]() ,
лежащих внутри области D,
то
,
лежащих внутри области D,
то![]() ,
где Г – граница области D.
,
где Г – граница области D.
ЗАДАНИЕ 11
Разложить функцию f(z) в ряд Лорана в окрестности изолированной особой
точки и определить характер этой особой точки.
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
7)
![]() 8)
8)
![]() 9)
9)
![]()
10)
![]() 11)
11)
![]() 12)
12)
![]()
13)
![]() 14)
14)
![]() 15)
15)
![]()
16)
![]() 17)
17)
![]() 18)
18)
![]()
19)
![]() 20)
20)
![]() 21)
21)
![]()
22)
![]() 23)
23)
![]() 24)
24)
![]()
ЗАДАНИЕ 12
При помощи вычетов вычислить интеграл.
1)
![]() 2)
2)
![]() 3)
3)
![]() 4)
4)
![]()
5)
![]() 6)
6)
![]() 7)
7)
![]() 8)
8)
![]()
9)
![]() 10)
10)
![]() 11)
11)
![]() 12)
12)
![]()
13)
![]() 14)
14)
![]() 15)
15)
![]() 16)
16)
![]()
17)
![]() 18)
18)
![]() 19)
19)
![]() 20)
20)
![]()
21)
![]() 22)
22)
![]() 23)
23)
![]() 24)
24)
![]()
Функциональный анализ §6 линейные пространства
Определение 1.
Пусть
H
–линейное пространство и
![]() .
Число
.
Число
![]() называется скалярным
произведением,
если выполняются следующие свойства:
называется скалярным
произведением,
если выполняются следующие свойства:
1.
![]() ;
;
2.![]() -число;
-число;
3.
![]() .
.
В пространстве
![]() -
квадратично интегрируемых функций
-
квадратично интегрируемых функций
![]() .
.
Определение
2.
![]() называется
нормой элемента
называется
нормой элемента
![]() .
.
В
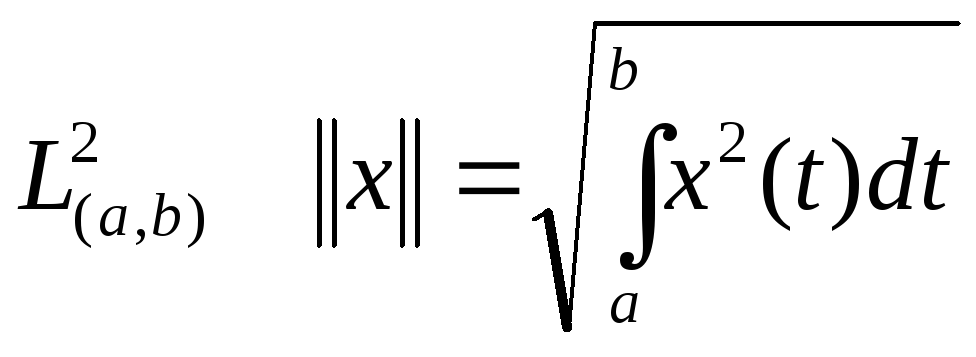 .
.
Неравенство
Коши-Буняковского:
![]() .
.
ЗАДАНИЕ 13
С помощью диаграмм Эйлера-Венна проверить справедливость утверждений:
![]()
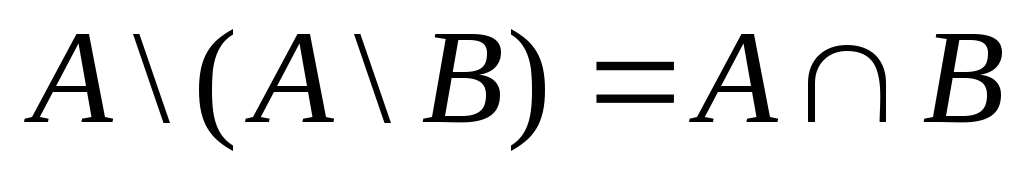
![]()
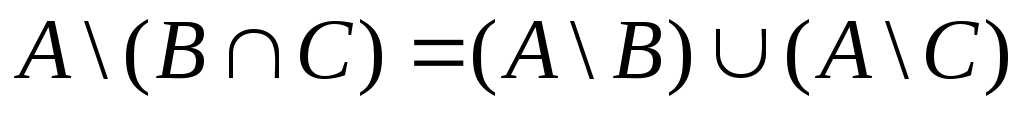
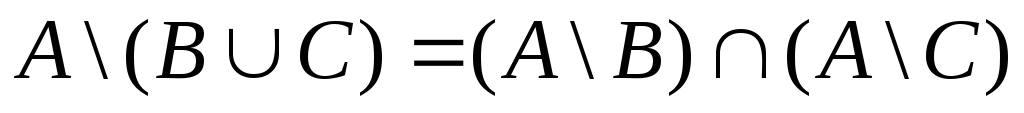
![]()
![]()
![]()
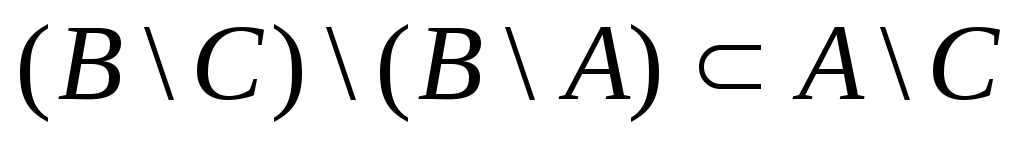
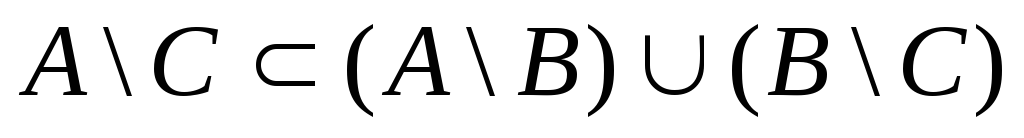
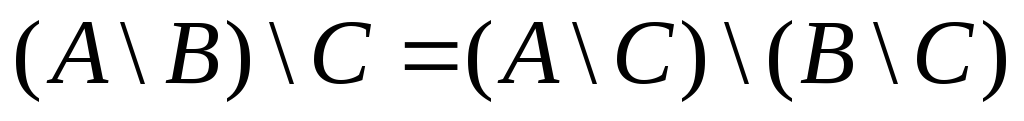
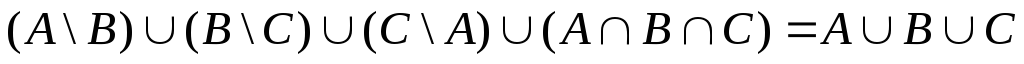
Если
![]() ,
то
,
то
![]() .
.
Если
![]() ,
то
,
то
![]() .
.![]()
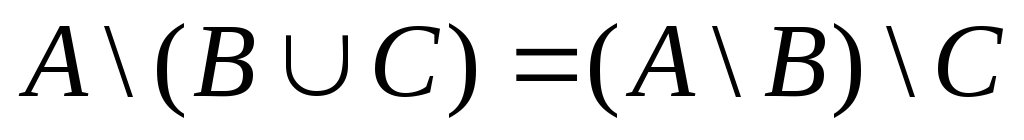
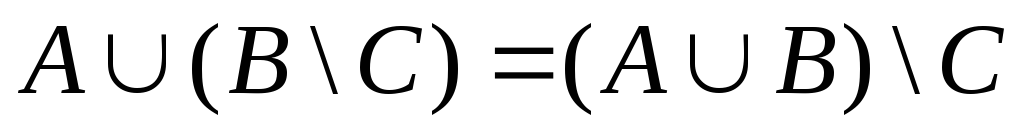
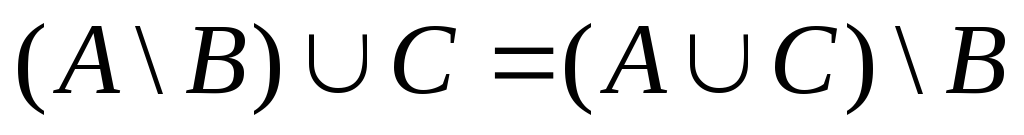
![]()
![]()
![]()
![]()
![]()
![]()
Если
![]() ,
то
,
то
![]() и
и
![]()
ЗАДАНИЕ 14
Вычислить скалярное
произведение
![]() в пространстве
в пространстве
![]() ,
если
,
если
1)
![]() 2)
2)
![]()
3)
![]() 4)
4)
![]()
5)
![]() 6)
6)
![]()
7)
![]() 8)
8)
![]()
9)
![]() 10)
10)
![]()
11)
![]() 12)
12)
![]()
13)
![]() 14)
14)
![]()
15)
![]() 16)
16)
![]()
17)
![]() 18)
18)
![]()
19)
![]() 20)
20)
![]()
21)
![]() 22)
22)
![]()
23)
![]() 24)
24)
![]()
ЗАДАНИЕ 15
Оценить скалярное произведение из задания 13 с помощью неравенства Коши-Буняковского.
§7 Ряды фурье
Ортогонализация по Шмидту состоит в следующем.
Пусть дана система элементов h1 ,h2,…, образующих базис в евклидовом пространстве Н. Построим из этих элементах ортонормированную систему
e1, e2,…
![]()
Функция, принадлежащая
пространству
![]() , раскладывается по системе ортогональных
функций:
, раскладывается по системе ортогональных
функций:
![]() в
ряд
в
ряд
![]() .
.
Коэффициенты Фурье вычисляются по формулам:
![]()
ЗАДАНИЕ 16
Применить процесс
ортогонализации к базису
![]() пространства R3.
Получить ортонормированный базис.
пространства R3.
Получить ортонормированный базис.
ЗАДАНИЕ 17
Разложить в ряд
Фурье периодическую функцию с периодом
Т=![]() .
.
1) y=
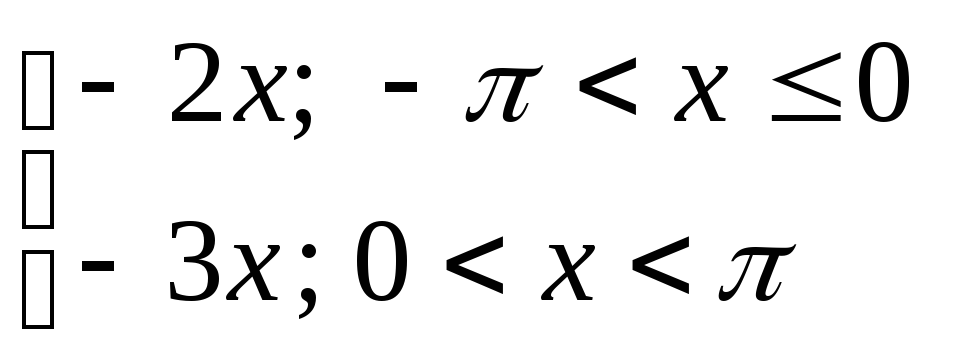 2) y=
2) y=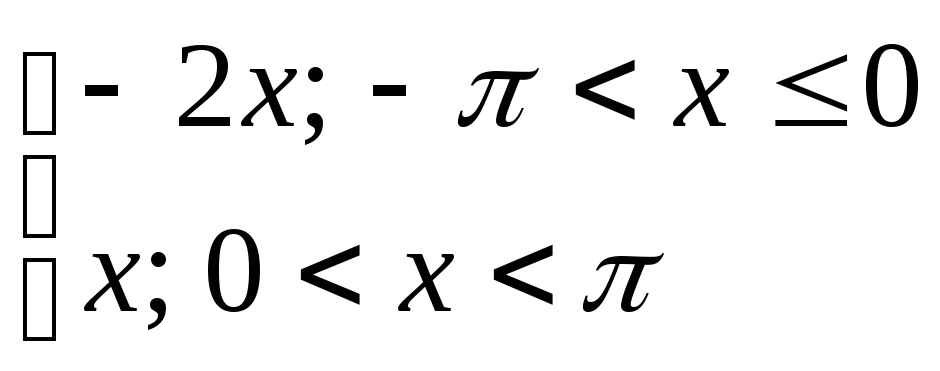 3) y=
3) y=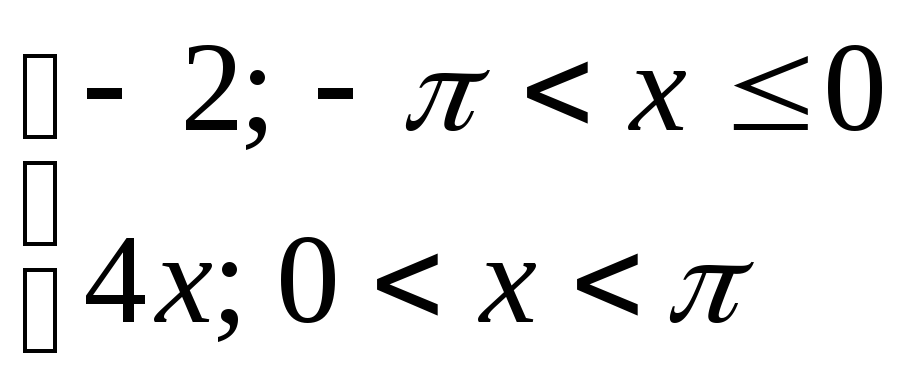
4) y=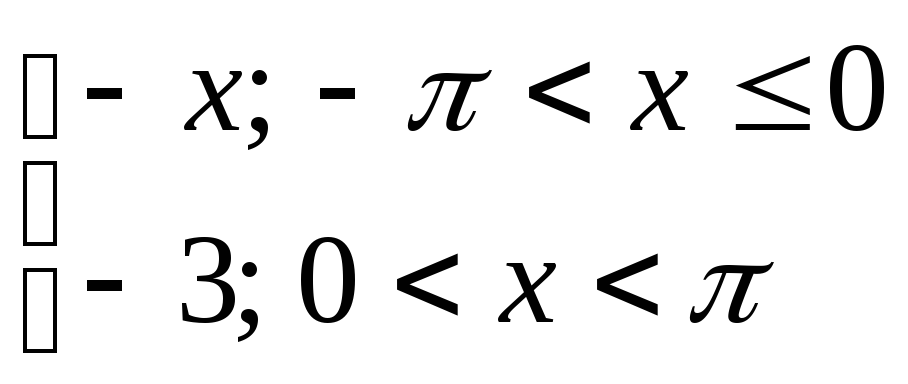 5) y=
5) y=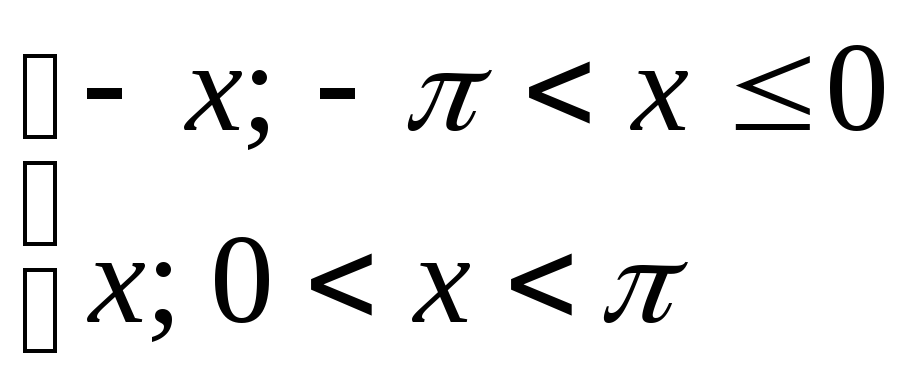 6) y=
6) y=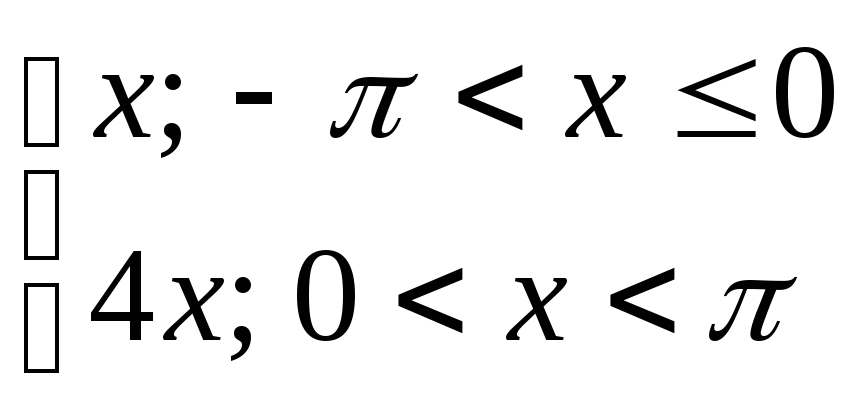
7) y=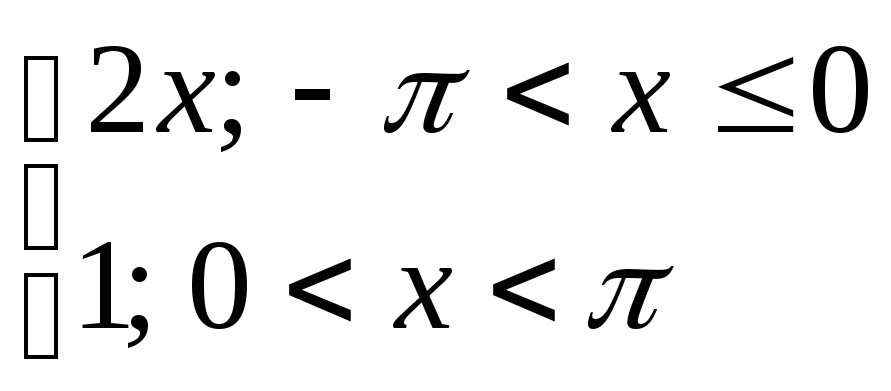 8) y=
8) y=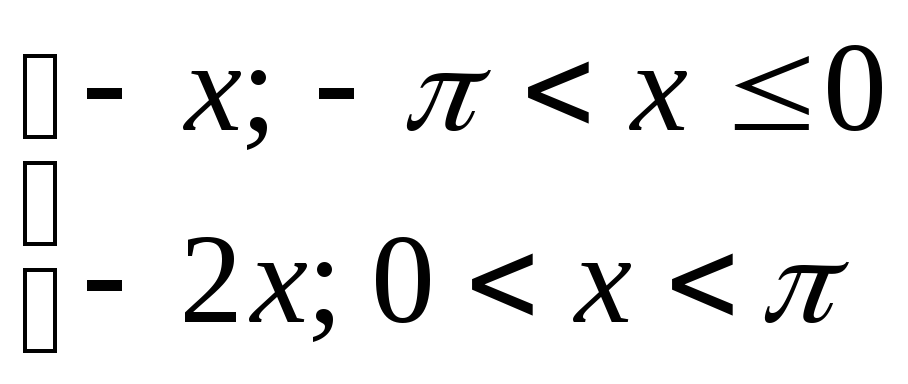 9) y=
9) y=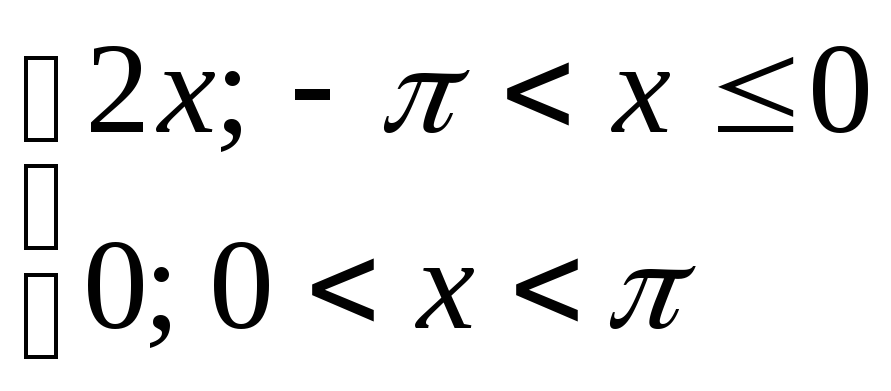
10) y=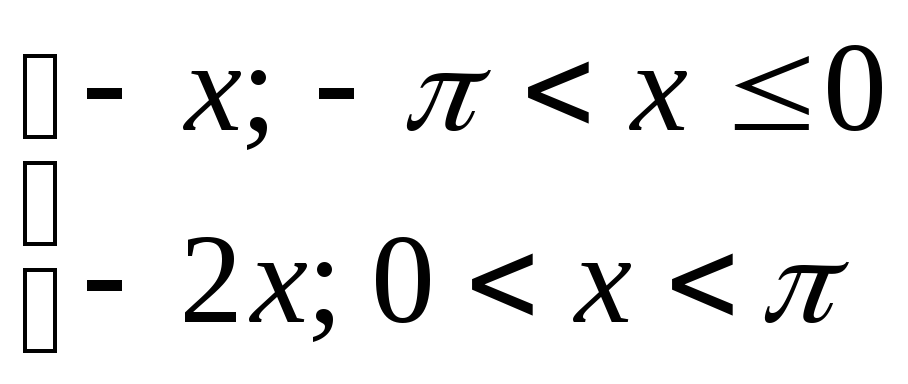 11) y=
11) y=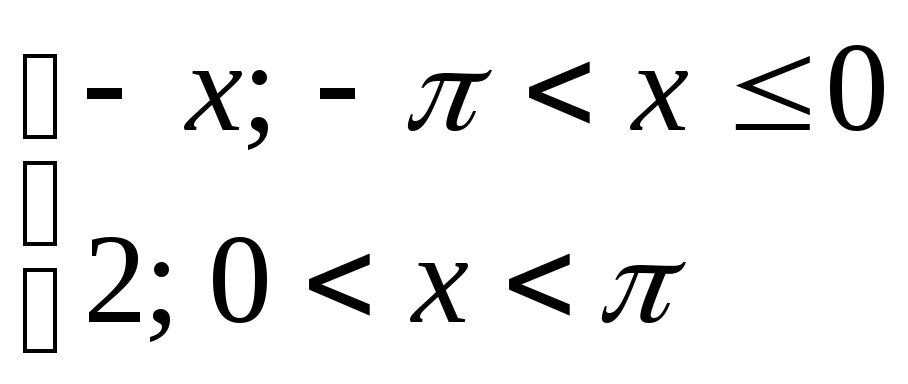 12) y=
12) y=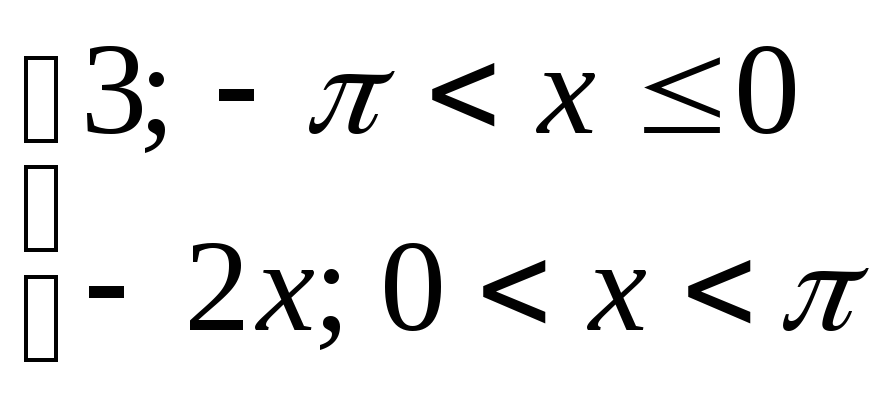
13) y=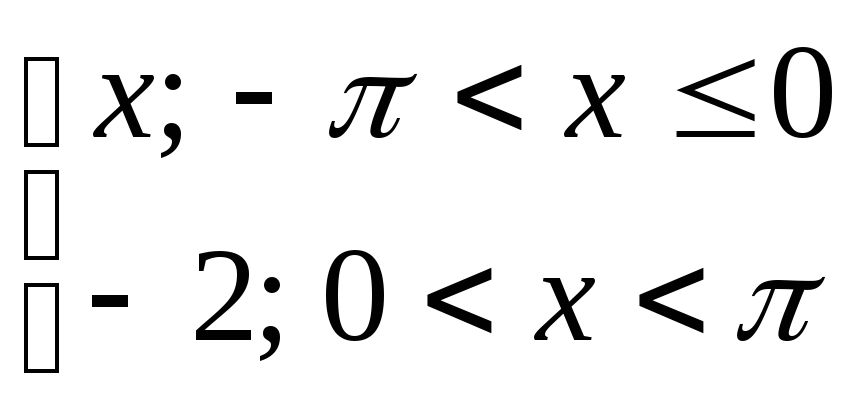 14) y=
14) y=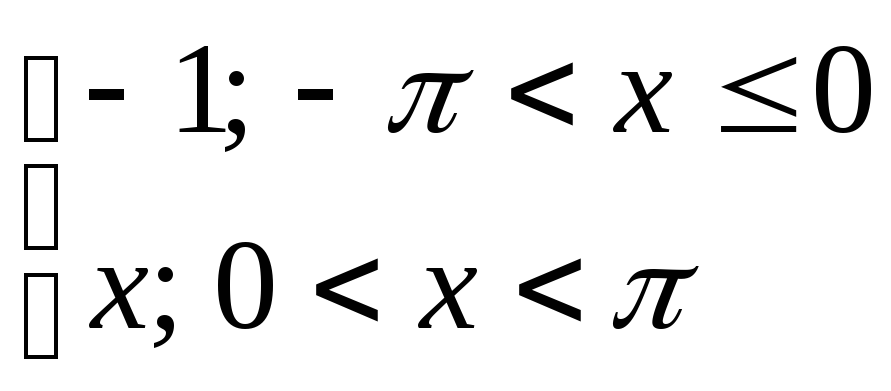 15) y=
15) y=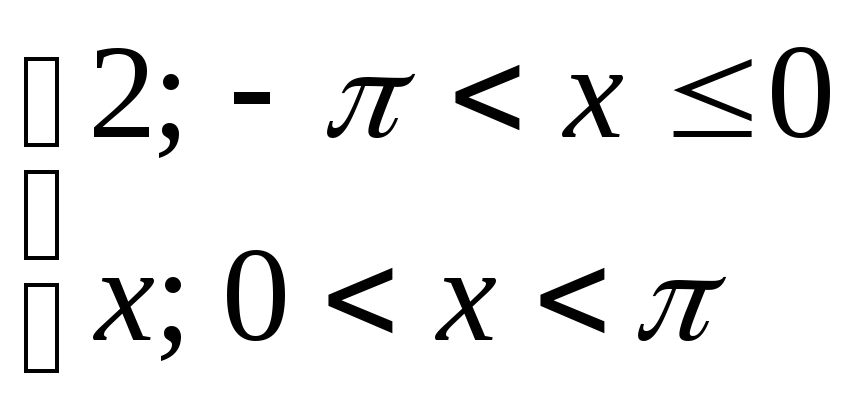
16) y=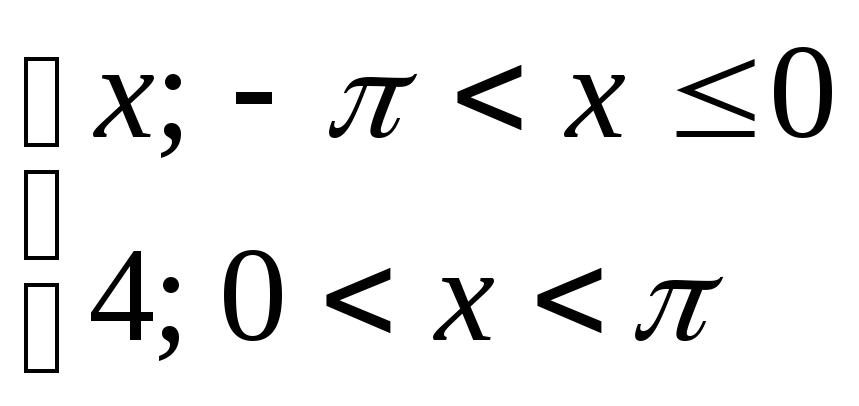 17) y=
17) y=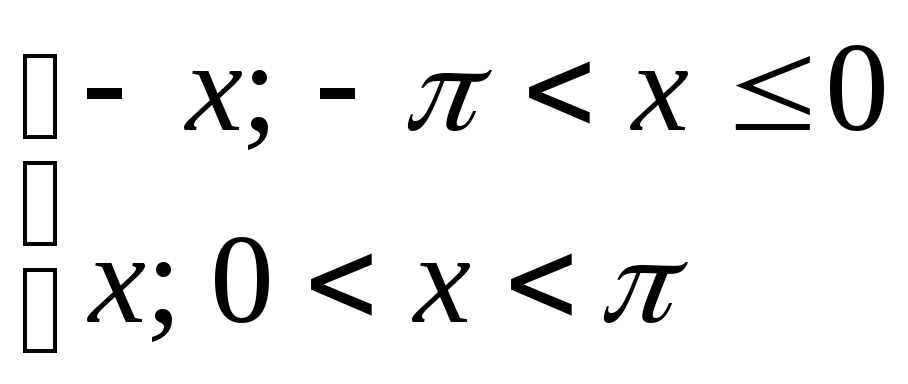 18) y=
18) y=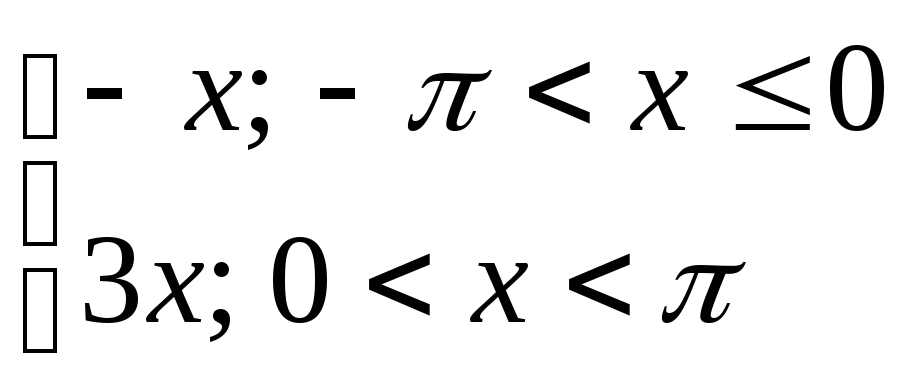
19) y=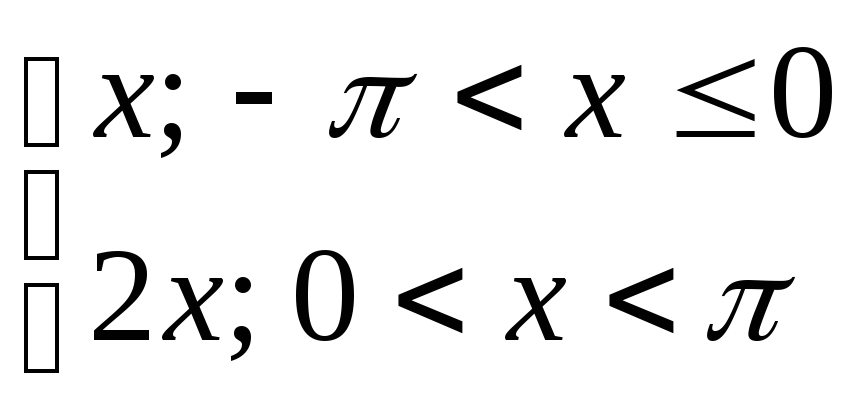 20) y=
20) y= 21) y=
21) y=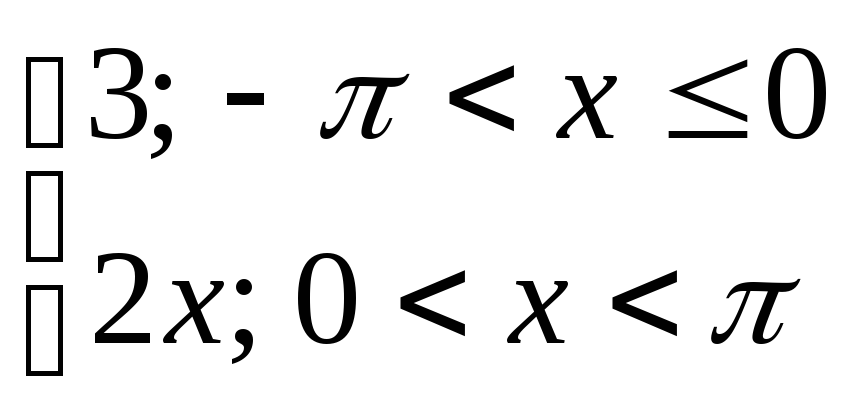
22) y=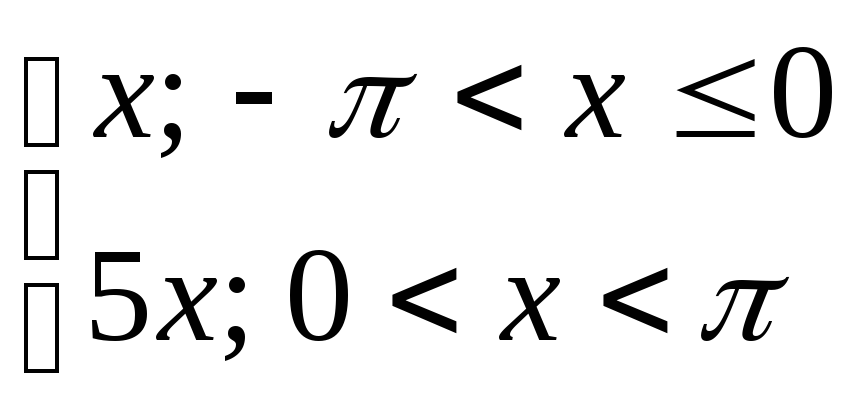 23) y=
23) y=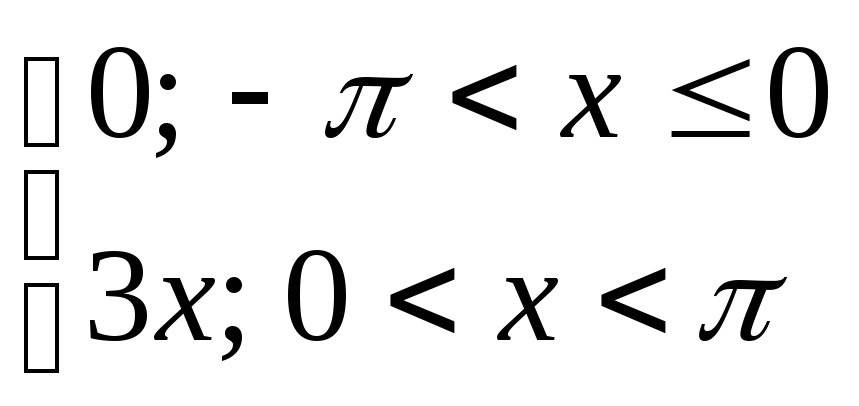 24) y=
24) y=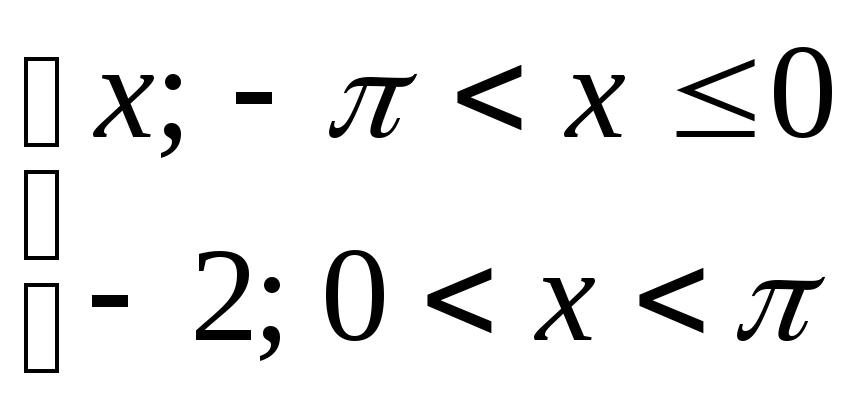
ЗАДАНИЕ 18
Разложить в ряд Фурье функцию.
1)
![]() 2)
2)
![]()
3)
![]() 4)
4)
![]()
5)
![]() 6)
6)
![]()
7)
![]() 8)
8)
![]()
9)
![]() 10)
10)
![]()
11)
![]() 12)
12)
![]()
13)
![]() 14)
14)
![]()
15)
![]() 16)
16)
![]()
17)
![]() 18)
18)
![]()
19)
![]() 20)
20)
![]()
21)
![]() 22)
22)
![]()
23)
![]() 24)
24)
![]()
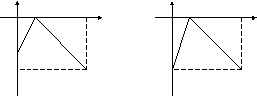
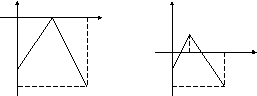
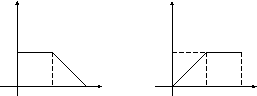
ЗАДАНИЕ 19
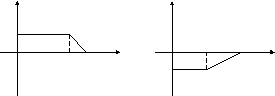
Доопределяя
необходимым образом заданную в промежутке
![]() функцию до периодической, получить для
неё ряд Фурье
функцию до периодической, получить для
неё ряд Фурье
a) по косинусам; б) по синусам.
 y
y


 y
0 1
4
y
0 1
4
x
-1
 2
2



 1
-3
1
-3
 0 1
3 x
0 1
3 x
18.1 18.2
 y
y
y
y
0 1 4 х 0 1 4 х
-2
-3 -3
18.3 18.4
 y
y
y
y
0 1 2 4
х 1
 0 3
0 3
-3 -1 1
-4 -2
18.5 18.6
 y
y
y
y
2
1
0 3 0 1 3
1 x -1 х
-2
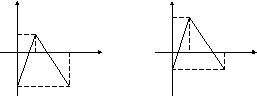
18.7 18.8
 y
y
y
y
1 x x
0 0 2 3
-1 2 3
-2
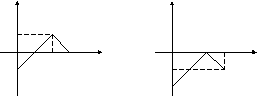
18.9 18.10
 y
y
y
y
1 1
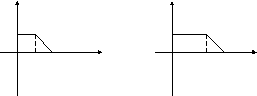
0 1 2 x 0 2 3 18.11 18.12
y y
2 2
0 2 4 х 0 2 4 х
18.13 18.14
 y
y
y
y
3 4
1 2
0 2 4 х 0 1 3 х
18.15 18.16
y y
2
0 2 4 5 х 0 1 3 4 х
-1 -1
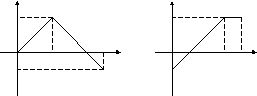
18.17 18.18
y y
2
 1
1
0 2 3 х 0 1 3 х
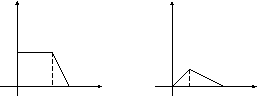
18.19 18.20
 y
y
y
y
2
1 1
0 1 3 x 0 2 3 x
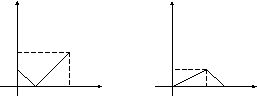
18.21 18.22
 y
y
y
y
1
0 3 4 х 0 2 4 х
-1
18.23 18.24
