
- •Рабочая программа дисциплины Математика 2
- •1. Цели освоения дисциплины
- •2.Место дисциплины в структуре ооп бакалавриата
- •3. Компетенции обучающегося, формируемые в результате освоения дисциплины «Математика 2»:
- •4. Структура и содержание дисциплины «Математика 2»
- •Раздел 1. Множества и функции.
- •Раздел 3. Интегралы и ряды.
- •Раздел 4. Функции нескольких переменных и дифференциальные уравнения.
- •5. Образовательные технологии
- •6. Оценочные средства для текущего контроля успеваемости, промежуточной аттестации по итогам освоения дисциплины и учебно-методическое обеспечение самостоятельной работы студентов
- •7. Учебно-методическое и информационное обеспечение дисциплины «Математика»
- •8. Материально-техническое обеспечение дисциплины «Математика»
Раздел 4. Функции нескольких переменных и дифференциальные уравнения.
Функции нескольких переменных. Функции двух переменных, их геометрическое изображение, линии уровня. Окрестность точки на плоскости. Расстояние между двумя точками на плоскости.Непрерывность функции двух переменных. Частное и полное приращение функции.
Непрерывность функции в точке и в области. Частные производные первого порядка. Геометрический смысл частных производных первого порядка. Полный дифференциал функции двух переменных. Теорема о связи дифференцируемости и непрерывности функции двух переменных. Теорема о представлении полного дифференциала. Достаточное условие дифференцируемости. Частные производные высших порядков. Теорема о независимости значения производной от порядка дифференцирования. Признак полного дифференциала. Экстремум функции двух переменных, точки экстремума. Необходимое условие экстремума. Критические точки. Достаточное условие экстремума. Условный экстремум.Применение частных производных в экономике.
Дифференциальные уравнения. Дифференциальное уравнение, его порядок. Решение дифференциального уравнения. Общее и частное решение дифференциального уравнения, интегральная кривая. Дифференциальные уравнения первого порядка. Дифференциальные уравнения первого порядка, нормальная форма. Задача Коши, начальные условия. Теорема о существовании и единственности задачи Коши. Уравнения с разделяющимися переменными. Линейные дифференциальные уравнения первого порядка. Однородные уравнения. Линейные дифференциальные уравнения высших порядков. Общие понятия. Задача Коши. Теорема о представлении общего решения. Линейные дифференциальные уравнения с постоянными коэффициентами. Общие понятия. Линейные дифференциальные уравнения с постоянными коэффициентами второго порядка. Характеристическое уравнение. Линейно зависимые решения. Теорема о представлении общего решения линейного однородного уравнения второго порядка. Дифференциальные уравнения в экономике.
|
|
Вопросы и задачи для самостоятельной работы 1. Пусть даны два множества:
Найти
2.
Даны два множества:
подмножеством другого? 3. Из сегмента[-3, 5] удален интервал (-3, 5). Что осталось? 4. Какова наибольшая окрестность нуля, содержащаяся в промежутке [-6, 5]? 5.Указать на числовой оси множества, заданные неравенствами:
6.
Какие значения
7.
Дана функция
8.
Дана функция
9.
Построить график функции
10. Найти область определения функций:
11. Какие из данных функций являются четными, какие нечетными:
|
|
|
|
|
|
|
|
12. Пользуясь определением предела числовой последовательности на языке
« »,
доказать, что последовательность
»,
доказать, что последовательность
 - бесконечно
- бесконечно
малая. Каково
должно быть N,
если
 ?
?
13. Является ли
последовательность
 сходящейся?
сходящейся?
14. Какие из точек x = - 2, x = 3, x = 5, x = 5,2 являются
предельными
точками множества
 ?
?
15.
Является ли функция
 бесконечно малой
бесконечно малой
при
 ?
?
-
Определить существует ли предел следующих функций:
 при
при
 ;
;
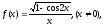 при
при
 .
.
17.
Непрерывна
ли функция
 на [-2,2]?
на [-2,2]?
18. Почему можно утверждать, что функция
 непрерывна
на множестве R?
непрерывна
на множестве R?
19. Установить, в каких точках и какого рода разрывы имеют
следующие функции:
 ,
,
 .
.
20.
Доопределить функцию
 в точке х=0 таким образом,
в точке х=0 таким образом,
чтобы она стала непрерывной в этой точке.
21.
Найти точки разрыва функции
 .
Построить график этой
.
Построить график этой
функции.
22.Можно ли утверждать, что квадрат разрывной функции есть также
разрывная
функция? Проверить это на примере
 .
.
-
Пользуясь определением производной, найти производные
следующих функций:
-
 ;
; -
 ;
; -
 .
.
24.
На параболе
 есть такая точка, в которой касательная
наклонена к положительному направлению
оси ОХ под углом 600.
Найти эту точку. Составить уравнение
касательной.
есть такая точка, в которой касательная
наклонена к положительному направлению
оси ОХ под углом 600.
Найти эту точку. Составить уравнение
касательной.
25. Найти дифференциалы следующих функций:
-
 ,
, -
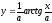 ,
, -
 .
.
26. Найти приближенно значение функций:
-
 при
х = 3,015;
при
х = 3,015; -
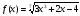 при
х = 1,001.
при
х = 1,001.
-
На сколько уменьшится величина степени 34, если основание
уменьшится на 0,0063?
-
Показать, что функция
 не является дифференцируемой
не является дифференцируемой
в точке х = 0.
-
Убедиться, что
 ,
но он не может быть вычислен
,
но он не может быть вычислен
с помощью правила Лопиталя. Почему?
-
В формуле Лагранжа о конечном приращении функции

определить
значение с:
 на отрезке [0,2].
на отрезке [0,2].
-
Можно ли на отрезке [-1,1] применить к функции

теорему Роля; теорему Лагранжа?
-
Доказать тождество
 при
при
 .
. -
Может ли значение функции в точке локального максимума
быть меньше значения функции в точке локального минимума?
-
Может ли монотонная функция иметь экстремум?
-
Может ли функция иметь экстремум в точке, в которой она
имеет перегиб?
-
Может ли иметь асимптоты и какие график ограниченной
функции?
-
Может ли иметь асимптоты и какие график функции, заданной
на ограниченном промежутке?
-
При каких значениях a и b точка (1;3) является точкой
перегиба
графика функции
 ?
?
-
Исследовать сходимость знакопостоянных рядов:
-
 ;
; -
 ;
;
-
 ;
; -
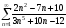 ;
; -
 ;
; -
 ;
; -
 ;
;
h)
 .
.
-
Решить дифференциальные уравнения с разделяющимися переменными:
-
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 ;
;
-
 ;
; -
 .
.
-
Решить задачу Коши для дифференциального уравнения:
 .
.
42.Определить порядок дифференциального уравнения:
а)
 ;
;
b)
 ;
;
c)
 .
.
43.Найти
дифференциальное уравнение, для которого
функция

является общим решением.
44.
Найти дифференциальное уравнение , для
которого функция
 является общим решением.
является общим решением.
45.
Найти дифференциальное уравнение , для
которого функция
 является общим решением.
является общим решением.
46.
Дано общее решение
 дифференциального уравнения.
дифференциального уравнения.
 .
Найти частные решения в случае:
.
Найти частные решения в случае:
а)

 ;
;
b)

 ;
;
c)

 .
.
47. Решить линейные однородные дифференциальные уравнения первого порядка.
а) ;
;
b)
 ;
;
c)
 .
.
48. Решить неоднородные линейные дифференциальные уравнения первого порядка.
a)
 ;
;
b)
 ;
;
c)
 ;
;
d) ;
;
e)
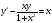 ;
;
f)
 ;
;
g)
 .
.
49. Решить задачу Коши:
a)
 (0,0);
(0,0);
b)
 (1,5);
(1,5);
c)
 (
( ,1);
,1);
d)
 (0,1);
(0,1);
e)
 (-1,1;
(-1,1;
f)
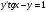 (
( ,1).
,1).
50. Показать, что заданная функция является решением (общим решением) дифференциального уравнения:
a)
 :
:
 .
.
b)
 :
:
 .
.
51. Является ли функция общим решением дифференциального уравнения?
a) :
:
 ;
;
b)
 :
:
 ;
;
c)
 :
:
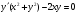 .
.



 .
.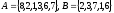 .
Какое из них является
.
Какое из них является
 .
. удовлетворяют одновременно неравенствам
удовлетворяют одновременно неравенствам ?
? .
Найти
.
Найти
 .
. .
Доказать, что
.
Доказать, что



 .
.