
- •Глава 2. Основные положения молекулярно-кинетической теории вещества
- •2.1. Молекулы, их поведение, масса, моль, число Авогадро
- •2.2. Основные законы гидростатики.
- •2.3. Применение основных законов гидростатики и аэростатики в физических измерениях
- •2.4. Закон идеального газа
- •2.5. Фазовые переходы
- •2.6. Основные положения термодинамики
- •2.7.Тепловые методы измерения вакуума
2.4. Закон идеального газа
Эмпирически были открыты законы, связывающие параметры газа. Состояние газа при относительно низком давлении описывается уравнением Бойля- Мариотта, которые независимо друг от друга вывели это уравнение опытным путем. При постоянной температуре произведение давления газа на его объем есть величина постоянная.
PV=const - закон Бойля-Мариотта
Это уравнение можно вывести на основании законов движения молекул газа, т.е. законов Ньютона. При этом газ рассматривают как систему частиц малого объема, не взаимодействующих друг с другом. Вычислим давление газа на стенку сосуда. В процессе взаимодействия молекулы со стенкой сосуда между ними возникают силы, подчиняющиеся третьему закону Ньютона. В результате проекция υx скорости молекулы, перпендикулярная стенке, изменяет свой знак на противоположный, а проекция υy скорости, параллельная стенке, остается неизменной (рис.2.7).
М олекула,
имеющая горизонтальную составляющую
импульса px,
упруго сталкиваясь со стенкой, отскакивает
от него в обратном направлении, при этом
она приобретает импульс -
px.
Таким образом, изменение импульса
молекулы в результате столкновения со
стенкой составляет 2px.
По закону сохранения импульса, такой
же импульс приобретает стенка сосуда.
За время t
давление оказывают молекулы, которые
находятся в пределах объема L
S,
где L=vx
t. Учитывая,
что F
= p / t=2mvx/
t
, можно определить давление, оказываемое
одной молекулой.
В
объеме содержащем N молекул, давление
на правую стенку оказывает N /2молекул,
т.к. половина молекул двигается вправо,
а половина влево.
олекула,
имеющая горизонтальную составляющую
импульса px,
упруго сталкиваясь со стенкой, отскакивает
от него в обратном направлении, при этом
она приобретает импульс -
px.
Таким образом, изменение импульса
молекулы в результате столкновения со
стенкой составляет 2px.
По закону сохранения импульса, такой
же импульс приобретает стенка сосуда.
За время t
давление оказывают молекулы, которые
находятся в пределах объема L
S,
где L=vx
t. Учитывая,
что F
= p / t=2mvx/
t
, можно определить давление, оказываемое
одной молекулой.
В
объеме содержащем N молекул, давление
на правую стенку оказывает N /2молекул,
т.к. половина молекул двигается вправо,
а половина влево.
Давление P= F/S= N/2∙2 mvx/ St = N m(vz)2 /vx St= N m(vх)2 /V; p= N m(vx)2/V; Молекулы имеют различную скорость, следовательно, мы должны приписать нашей скорости индекс «ср».
По теореме Пифагора в трехмерном пространстве
(v2)ср.=(
vx)2
ср
+ (vy)2
ср
+ (vz)2
ср
=3(vx)2
ср;
.(
vx)2
ср=(v2)ср./3;
отсюда следует  ,
где
n=N/V
– концентрация молекул газа. Тройка в
знаменатели показывает, что молекула
газа может двигаться независимо по трем
направлениям, или, как говорят, молекула
обладает тремя степенями свободы.
,
где
n=N/V
– концентрация молекул газа. Тройка в
знаменатели показывает, что молекула
газа может двигаться независимо по трем
направлениям, или, как говорят, молекула
обладает тремя степенями свободы.
Это уравнение называют основным уравнением молекулярно-кинетической теории газа. Его можно записать в виде PV=2/3NЕкин. ср.
Полученный закон устанавливает соотношения параметров газа, называемого идеальным, следовательно константа в уравнении Бойля- Мариотта (PV=const.) равна 2/3NЕкин. ср.
C другой стороны, закон справедлив при постоянной температуре T=const. Таким образом, имеется связь между температурой и средней кинетической энергией молекул.
Понятие температуры. Температура характеризует степень нагретости тела. Для определения температуры необходимо сравнить степень нагретости по отношению к другому телу. Если два тела с разной степенью нагретости привести в соприкосновение, то некоторое время будут меняться их параметры (объем, давление, плотность, размеры, при этом могут изменяться не все параметры, а какие-то из них поддерживаться постоянными). Через какое-то время эти параметры перестанут изменяться. Состояние тел, при котором их макроскопические параметры остаются неизменными называется термодинамическим равновесием. Температуры тел, находящихся в термодинамическом равновесии, считают одинаковыми. На этом основано измерение температуры, например, жидкостным термометром – когда объем жидкости в термометре перестанет меняться, считают, что его температура такая же, как у тела, с которым он соприкасается. Для определения значения температуры используют температурные шкалы. Одной из таких шкал является шкала Цельсия, в которой температуру тающего льда приняли за 0, а кипящей воды за 100 градусов. Шкалу между этими точками разделили на 100 равных частей и продолжили в обе стороны. Температура в градусах Цельсия фигурирует в законах Гей-Люссака и Шарля, которые как и закон Бойля-Мариотта были открыты опытным путем:
Закон Гей-Люссака При неизменном давлении объем данного количества газа прямо пропорционален температуре: V~T , при Р=const. V = V0·(1 + α·t), где V – объем газа при температуре t°С; V0 – его объем при 0°С.
Величина α называется температурным коэффициентом объемного расширения. Для всех газов a = (1/273°С–1, точнее 1/273,15°С–1.
Закон Шарля При постоянном объеме давление газа прямо пропорционально абсолютной температуре: Р~T, при V=const; р = р0(1+γt).
Здесь р– давление газа при температуре t, °С; р0 – его давление при 0 °С.
Величина γ называется температурным коэффициентом давления. Ее значение не зависит от природы газа; для всех газов γ = 1/273,15 °С–1.
Установленная этим законом зависимость используется в газовом термометре, в котором мерой температуры газа является его объем.
Из
закона Шарля следует, что при t=-2730С
давление идеального газа обращается в
0. Температурная шкала, в которой за 0
принята температура -273,15 0С
называется абсолютной или шкалой
Кельвина. Цена деления шкалы кельвина
совпадает с ценой деления шкалы Цельсия.
Из закона Шарля следует, что давление
данной массы газа пропорционально его
абсолютной температуре, если объем газа
остается постоянным. 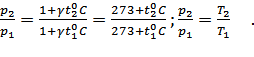 Аналогично
из закона Гей- Люссака следует
Аналогично
из закона Гей- Люссака следует  при постоянном давлении.
при постоянном давлении.
Связь
абсолютной температуры с кинетической
энергией молекул.
В
постоянном объеме и при нормальном
давлении и температуре (р0=105Па;
Т0=273К)
концентрация молекул газа ![]()
![]() -
молярный объем при нормальных условиях.
При изменении температуры до величины
Т давление изменится до давления,
равного:
-
молярный объем при нормальных условиях.
При изменении температуры до величины
Т давление изменится до давления,
равного: ![]() .
используя это уравнение и уравнение
идеального газа
.
используя это уравнение и уравнение
идеального газа ![]() ,
можно
получить соотношение -
,
можно
получить соотношение -  ;
где к
;
где к![]() – постоянная Больцмана.
к=1.38* 1023
Дж/К
.
– постоянная Больцмана.
к=1.38* 1023
Дж/К
.
Таким
образом, средняя кинетическая энергия
молекул может служить определением
температуры и ее значения можно было
бы выбрать в качестве температурной
шкалы. Но температурную шкалу выбрали
иначе, поэтому постоянную Больцмана
можно рассматривать как переводной
коэффициент для перевода температуры
из энергетических единиц в привычные
градусы температурной шкалы.
Средняя
кинетическая энергия молекул, выраженная
через температуру имеет вид![]()
Уравнение
![]() ,
учитывая
приведенные соотношения, можно записать
в виде p=nkT
или pV=NkT,
где V
– объем газа, N
– количество молекул газа.
,
учитывая
приведенные соотношения, можно записать
в виде p=nkT
или pV=NkT,
где V
– объем газа, N
– количество молекул газа.
Для одного моля газовый закон приобретает вид pVμ=NakT или pVμ =RT, где Vμ – молярный объем; величина R= Nak носит название универсальной газовой постоянной. Универсальная газовая постоянная не зависит ни от рода газа, ни от его состояния.
Т.к.
Vμ=V/ν,
где ν
– количество вещества и равно отношению
массы к молярной массе m/
М,
то ![]() Эта форма записи носит название
(закона)
Менделеева — Клапейрона.
Эта форма записи носит название
(закона)
Менделеева — Клапейрона.
Часто в процессах один из макропараметров газа остается постоянным. При этом уравнение состояния газа приобретает более простой вид. В зависимости от того какой параметр поддерживается постоянным процесс называют изохорным (постоянный объем), изобарическим (постоянное давление), изотермическим (постоянная температура).
Зависимости макроскопических параметров газа можно представить графически – изохоры, изобары, изотермы.
И деальный
и реальный газ. Уравнение
Бойля –Мариотта достаточно хорошо
описывало поведение газов при достаточно
низких давлениях. Для более высоких
давлений и для газов с более сложным
составом молекул наблюдались отклонения
от рассмотренного уравнения. Более
точное уравнение было найдено
Ван-дер-Ваальсом и имеет вид:
деальный
и реальный газ. Уравнение
Бойля –Мариотта достаточно хорошо
описывало поведение газов при достаточно
низких давлениях. Для более высоких
давлений и для газов с более сложным
составом молекул наблюдались отклонения
от рассмотренного уравнения. Более
точное уравнение было найдено
Ван-дер-Ваальсом и имеет вид: ![]() .
.
Уравнение Ван-дер-Ваальса содержит поправки а и б, физический смысл которых был найден тем же Ван-дер-Ваальсом. Он предположил, что на малых расстояниях r между молекулами действуют силы отталкивания, которые с увеличением расстояния сменяются силами притяжения. Кроме того, молекулы имеют объем, который не учитывается в уравнении идеального газа. Таким образом, поправка b учитывает объем, которые занимают сами молекулы, а поправка а – взаимодействие самих молекул. Практически идеальным можно считать одноатомный газ при малых давлениях.
