
- •Глава 3. Инструментальные средства моделирования
- •3.2.2 Пользовательский интерфейс
- •3.2.3. Создание, редактирование и отладка м-файлов
- •3.2.3 Простейшие вычисления
- •Элементарные математические функции
- •Функции, определенные пользователем
- •3.2.4 Массивы в matlab
- •3.2.5 Основные матричные операции
- •3.2.6 Графики в matlab Построение двумерных графиков
- •Операторы цикла Оператор for … end
- •Цикл while
- •Обработка массивов и матриц средствами м-языка
- •Отладка м-программ в matlab
- •Численное решение математических задач в matlab
- •Численное интегрирование
- •Символьные вычисления в matlab
- •Вычисление производной
Символьные вычисления в matlab
Основные символьные операции
Объявить символьную переменную в Matlab можно двумя способами:
Способ 1. С помощью команды syms. Таким способом можно объявить сразу несколько символьных переменных. Синтаксис команды syms:
syms name1 [name2 …] [options],
где name1, [name2 …] – имена создаваемых переменных. С помощью опции options можно указать, как интерпретировать переменные: real – для вещественных переменных, unreal – для комплексных.
Имена должны начинаться с буквы и содержать только буквы и цифры.
Используя обычные арифметические операции и функции, можно создавать новые символьные выражения и функции.
Пример 3-13. Требуется создать символьную функцию
![]()
|
Инструкции |
Результат |
|
>> syms x y >>% создание символьной функции f >> f = (x^2 + 2*y)/(2*sin(x)-cos(2*y)) |
f = (x^2 + 2*y)/(2*sin(x)-cos(2*y)) |
Способ 2. Объявить символьную переменную в Matlab можно с помощью функции sym. Синтаксис команды sym:
[name] = sym( name [, options]),
Последовательность функций u=sym(u); v=sym(v); эквивалентна команде syms u v. Опция options принимает те же значения, что и в команде syms. Но в отличие от команды syms, функцию sym можно использовать для создания символьных функций или выражений.
Пример 3-13. Требуется создать символьную функцию
F(x, y) = x2 – 2y
|
Инструкции |
Результат |
|
>> % объявление символьных переменных x и y >> х=sym('x'); y=sym('y'); >> f = x^2-2*y
Возможно создание символьной функции без предварительного объявления символьных переменных: >> f = sym( 'x^2-2*y' ) |
f = x^2-2*y
f = x^2-2*y |
Вычисляет значение символьного выражения или переменной функция Name=vpa(expr[,n])),
где expr – символьное выражение или переменная, n задает точность вычислений (по умолчанию n =32)
Пример 3-14. Требуется вычислить значение
символьной функции
![]() при х = , и у
= .
при х = , и у
= .
|
Инструкции |
Результат |
|
>> syms x y >> x=pi; >> y=pi; >>vpa((x^2+2*y)/(2*sin(x)-cos(2*y)),3) |
ans = -16.153 |
Решение уравнений и систем в символьном виде
Для решения уравнений и систем в символьном виде в Matlab существует функция solve(ex1, ex2, …,exN, var1, var2, …, varN). Она возвращает значения переменных (ex1, ex2, …,exN), при которых соблюдаются равенства, заданные выражениями ex1, ex2, …,exN.
Пример 3-15. Требуется найти корни полинома х3 - 6 х2 +11 x - 6 = 0
|
Инструкции |
Результат |
|
>> syms x >> y = solve(x^3-6*x^2+11*x-6, x)
|
y = 1 2 3 |
Пример 3-16. Требуется решить систему нелинейных уравнений:
![]()
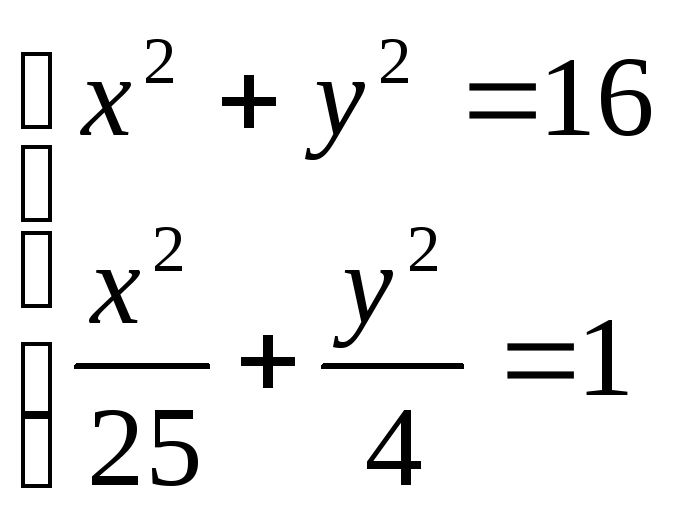
|
Инструкции |
Результат |
|
>> syms x y >> f1=sym('x^2+y^2-16'); >> f2=sym('x^2/25+y^2/4-1'); >> %Аналитическое решение системы: >> [x,y]=solve(f1,f2,x,y)
>>%Численное решение системы >> vpa([x,y],4)
|
x = 10/7*7^(1/2) -10/7*7^(1/2) 10/7*7^(1/2) -10/7*7^(1/2) y = 2/7*21^(1/2) 2/7*21^(1/2) -2/7*21^(1/2) -2/7*21^(1/2) ans = [ 3.781, 1.309] [ -3.781, 1.309] [ 3.781, -1.309] [ -3.781, -1.309] |
Вычисление пределов
Для вычисления пределов в Matlab предусмотрена функция limit. В общем случае синтаксис этой функции: limit ( F[, x, b, options ]), где F – имя символьной функции или ее символьная запись, x – аргумент функции, b – значение, к которому стремится x. Если х стремится к бесконечности (к минус бесконечности), параметр b принимает значение inf (-inf). С помощью опции options можно указать, предел функции в точке b слева (left) или справа (right) требуется вычислить.
Пример 3-17. Требуется вычислить предел
функции
![]()
|
Инструкции |
Результат |
|
>> syms x >> f=sym('log(5-2*x)/((10-3*x)^(1/2)-2)'); >> limit(f,'x',2) |
ans = 8/3 |
Пример 3-18. Требуется вычислить пределы функции
![]() и
и
![]()
|
Инструкции |
Результат |
|
>> syms x >> f=sym('(x^2-57*x+572)/(abs(x-44)*(x^2-(53/4)*x+13/4))'); >>% вычисляем предел функции в точке х44 слева: >> limit(f,x,44,'left') >>% вычисляем предел функции в точке х44 справа: >> limit(f,x,44,'right') |
ans = -4/175
ans = 4/175 |
Задание 3-6. Вычислите пределы функций:
1.
![]()
2.
![]()
3.
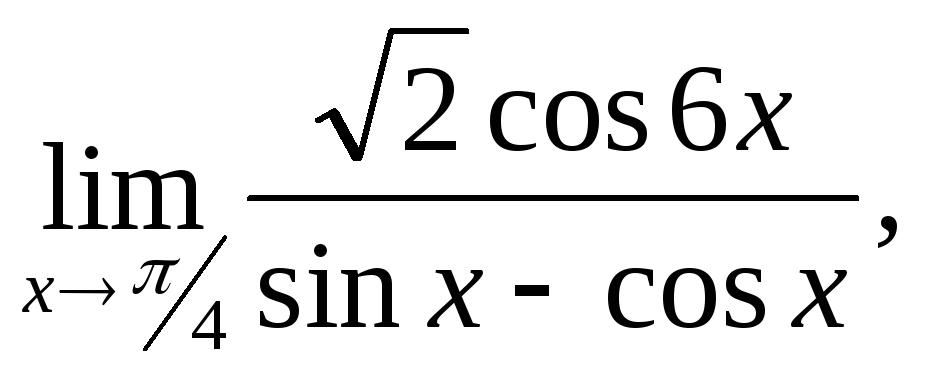
4.
![]()
5.
![]()
