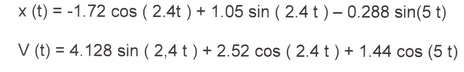Решение

Рассмотрим первый случай свободных гармонических колебаний без учета сил сопротивления.

Рассчитаем суммарную жесткость системы пружин C1.C2.C3.

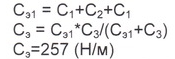
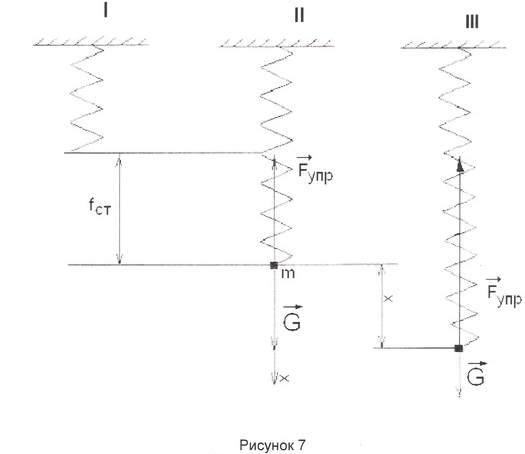
Примем груз за материальную точку, ось X направим параллельно пружинам, связав ее с положением статистического равновесия. Начальные условия при t=0 На груз действует сила трения G_T и сила упругости F_ynp . Известно, что сила упругости пропорциональна жесткости. Запишем дифференциальное уравнение второго порядка откуда

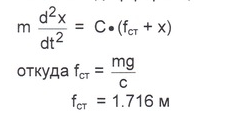
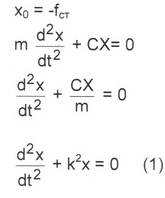Здесь введено обозначение

к - частота свободных колебаний

к = 2.4

Решение этого уравнения можно искать в виде х = exp(z*t) После подстановки этого выражения в (1) получаем характеристическое уравнение для (1)

z² + к² = О

Это квадратное уравнение имеет два мнимых корня z, = ik ;z₂ = -i k

Тогда решение (1) можно представить в виде

х = Ci cos (k t) + C2 sin (k t)

Константы находятся из начапьных условий при t = О

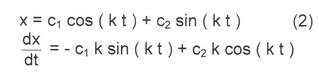
После подставления начальных условий

Откуда получаем с, = х₀

Период колебаний

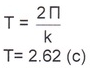
Решение имеет вид

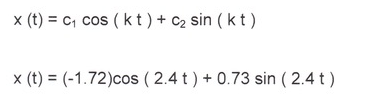
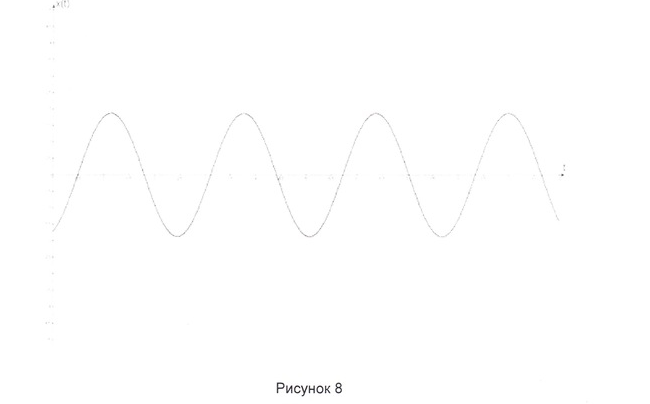
Скорость имеет вид

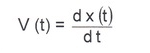
V (t) = - 4.128 sin ( 2.41) - 1.752 cos ( 2.4 t)

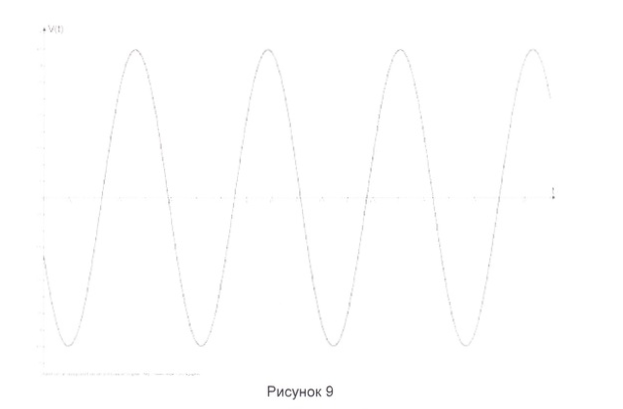
Амплитуда колебаний:

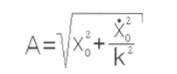
А=1.87(м)

Результаты

Уравнение для координаты и скорости

х (t) = (-1,72)cos ( 2.4 t) + 0.73 sin ( 2.4t)

V (t) = -4.128 sin (2.41) -1.752 cos ( 2.4t)

Собственная частота колебаний

Период колебаний

Т= 2.62 (с)

Амплитуда колебаний

А = 1.87 (м)

Этап III. Свободные затухающие колебания.

Рассмотрим второй случай - затухающие колебания с учетом сил сопротивления.

Уравнение Лагранжа второго рода применительно к этому случаю имеет вид

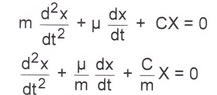
Уравнение движения груза имеет вид

где - коэффициент сопротивления В результате введения в уравнение сил сопротивления возможны три случая: большого сопротивления b > к, малого b < к и предельного к = b сопротивления,

к = 2.4 b = 0.85

У нас случай малого сопротивления, поскольку b < к

Решение уравнения (3) можно искать в виде х = ехр (А • t)

После подстановки этого выражения в (3) получаем

характеристическое уравнение для уравнения (3)

Это квадратное уравнение имеет 2 корня:

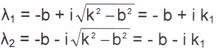
где

Тогда решение (3) можно представить в виде

Константы находятся из начальных условий при t = 0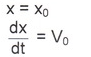

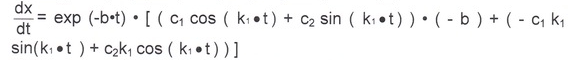После подставления начальных условий

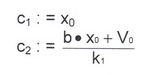
Решение имеет вид

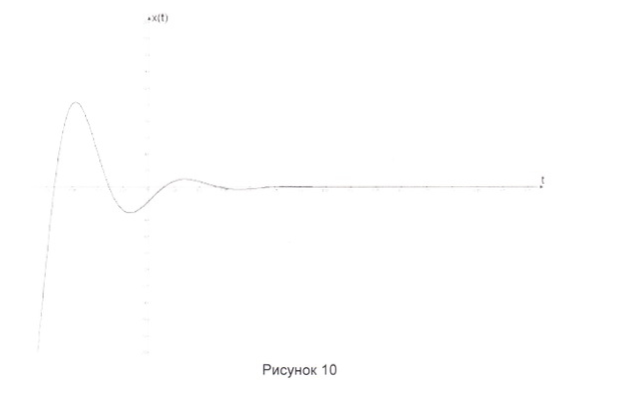
Видно, что при стремлении t к бесконечности ж стремится к 0.

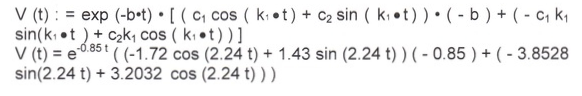
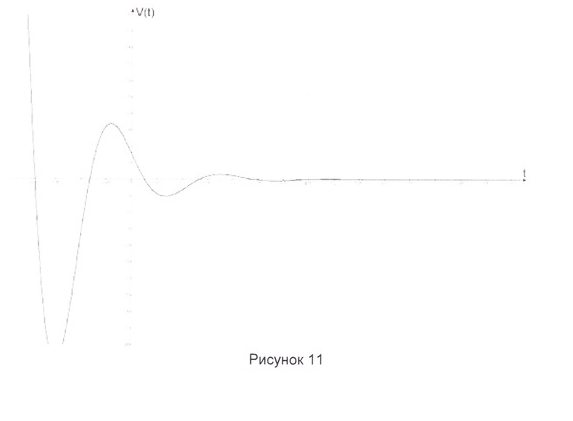
Амплитуда колебаний и фаза колебаний:

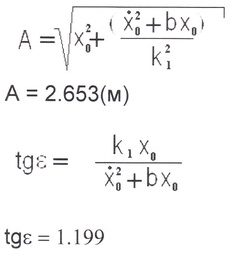
Период затухающих колебаний

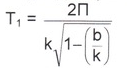
Декремент затухания

Уравнения движения груза через экспоненты:

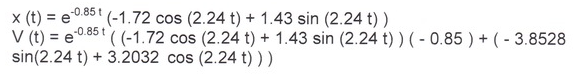
Декремент затухания

Период затухающих колебаний

Этап IV. Вынужденные колебания без учета сил сопротивления. Колебательная система изображена на рисунке 12

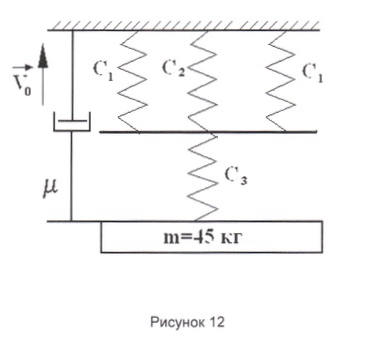
Исходные данные задачи:

V₀: = 1.75 (м/с)

С, : =210 (Н/м)

С₂: = 300 (Н/м)

С₃ : = 400 (Н/м)

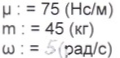
По заданным исходным данным и расчетной модели найти:

• Амплитуду колебаний, собственную частоту, период, закон колебаний.

• Построить графики x(t) и V(t).

• Составить дифференциальное уравнение с учетом сил сопротивления, определить коэффициент сопротивления, коэффициент собственной частоты и сравнить их между собой.

Решение

Рассмотрим вынужденные колебания без учета сил сопротивления. Вынуждающая сила

Суммарная жесткость системы пружин рассчитывалась во втором этапе

С : = 257 (Н/м) Начальные условия при t = О

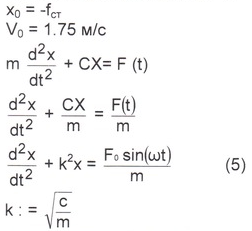
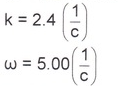
Решение уравнения (5) можно искать в виде суммы двух решений: решение однородного уравнения х, и решение неоднородного х₂. Однородное уравнение для определения х,

Это уравнение совпадает с дифференциальным уравнение

собственных колебаний, поэтому

Определение x₂ зависит от соотношения между и к. В нашем случае, отлична от к, что означает отсутствие резонанса. Частное решение х₂ будем искать в виде

Подставим частное решение (7) в уравнение (5), получим тождество, справедливое в любой момент времени. Посчитаем соответствующее произведение

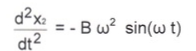
Уравнение (5) после подстановки (7) имеет вид

Если перенести все слагаемые в левую часть и преобразовать, получим

Поскольку синус переменного аргумента равен нулю не для всех значений t, то полученное тождество выполняется, если постоянный коэффициент в скобках при синусе равен нулю:

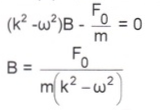
Итак

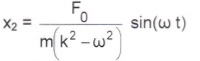
Таким образом:

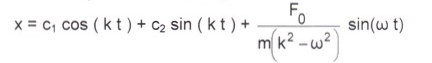
В амплитудной форме

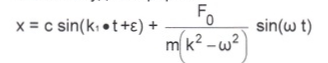
Константы находятся из начальных условий при t = 0

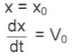
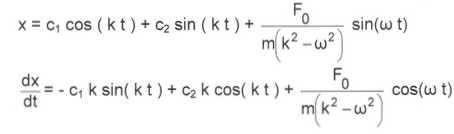
После подставления начальных условий

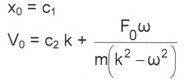
Откуда следует

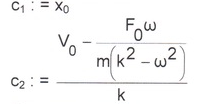
Решение имеет вид

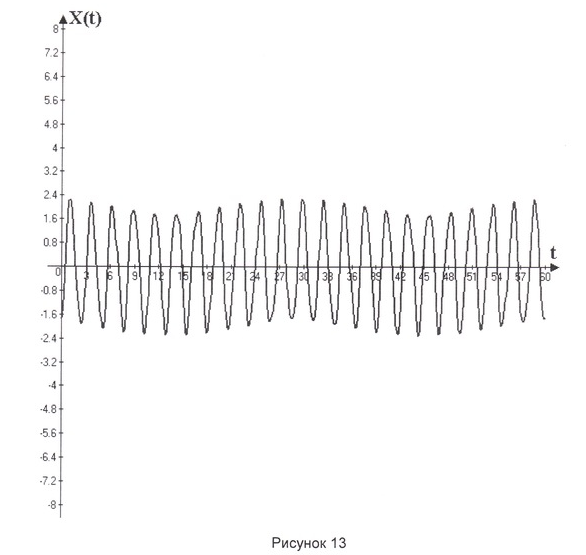
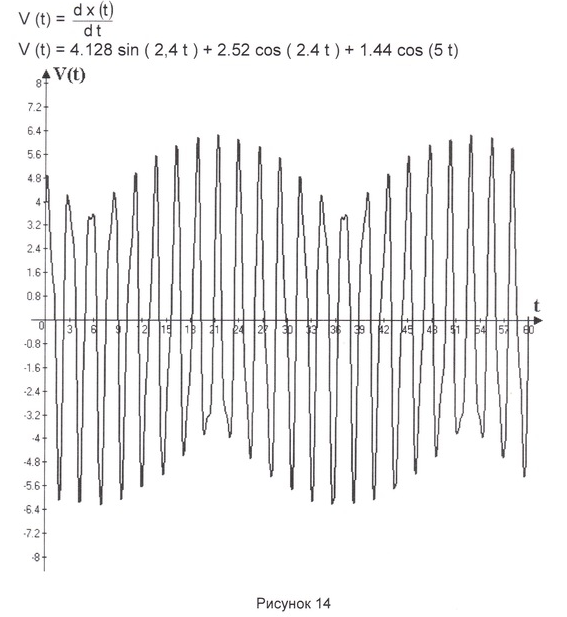
Амплитуда собственных колебаний и начальная фаза

Результаты

Уравнения для координаты и скорости