
- •Содержание
- •Введение
- •1 Рабочая программа по дисциплине «информатика»
- •Раздел 2. Алгоритмизация и программирование
- •2 Основы алгоритмизации
- •2.1 Основные этапы подготовки и решения задачи на компьютере
- •2.2 Постановка задачи. Разработка математической модели
- •2.3 Алгоритм и его свойства
- •2.4 Форма записи алгоритма на естественном языке
- •2.5 Графическая форма записи алгоритма
- •2.6 Типовые вычислительные процессы и структуры алгоритмов
- •2.6.1 Линейный вычислительный процесс
- •2.6.2 Разветвляющийся вычислительный процесс
- •2.6.3 Циклический вычислительный процесс
- •2.6.4 Алгоритмы обработки одномерных информационных массивов
- •2.6.5 Алгоритмы обработки двумерных информационных массивов
- •3 Язык программирования vba
- •3.1 Элементы языка
- •3.2 Программирование алгоритмов линейной структуры
- •3.3 Программирование алгоритмов разветвленной структуры
- •3.4 Программирование алгоритмов циклической структуры
- •3.5 Организация программ обработки одномерных массивов
- •3.6 Организация программ обработки двумерных массивов
- •4 Контрольная работа и методические указания по её выполнению
- •4.1 Выбор варианта
- •4.2 Задание 1. Варианты задач
- •4.3 Задание 2. Варианты задач
- •4.4 Задание 3. Теоретический вопрос
- •4.5 Методические указания по выполнению контрольной работы
- •4.5.1 Пример выполнения задания 1
- •4.5.2 Пример выполнения задания 2
- •4.5.3 Пример выполнения задания 3
- •Вопросы для подготовки к экзамену
- •Программирование алгоритмов циклической структуры.
- •Литература
- •Указатель
- •650992, Г. Кемерово, пр. Кузнецкий, 39. Тел. 25-75-00.
2.6.5 Алгоритмы обработки двумерных информационных массивов
Многомерные массивы широко используются в статистике и математике, такие массивы имеют более одного измерения (индекса). Таким образом, двумерный массив представляет собой набор данных одинакового типа, в котором доступ к любому его элементу осуществляется по двум индексам: номеру строки и номеру столбца. Количество индексов определяет размерность массива. Например, размерность двумерного массива равна произведению числа строк на число столбцов. Двумерные массивы являются логической структурой данных удобной для решения задач связанных с обработкой величин зависящих от двух параметров.
Элемент многомерного массива обозначается именем массива с индексами, например, Х(i, j). Индексы представляют собой выражения целого типа. Обращаться к элементам массива можно в произвольном порядке, задавая значения индексов. Причем, первый индекс всегда нумерует строки, второй столбцы.
Для того чтобы обработать элементы массива (присвоить, ввести, вывести значения), необходимо организовать вложенные циклы, в которых перебираются все комбинации значений индексов.
Рассмотрим пример алгоритма реализующего ввод двумерного массива по строкам в виде блок-схемы (рис. 18):
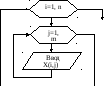
Рис. 18 Фрагмент блок-схемы ввода двумерного массива по строкам
В этом примере элементы массива вводятся по строкам в следующем порядке:
Х11, Х 12,..., Х 1m
Х 21, Х 22,..., Х 2m
.......................
Хn1, Х n2,..., Х nm
Для каждого значения счетчика внешнего цикла i, вложенный цикл выполняется заданное количество (m) раз.
Пример 10. Выпуск продукции в тыс. руб. представлен таблицей
Таблица 4 – Исходные данные для примера 10
|
№ месяца Вид продукции |
1 |
2 |
3 |
… |
|
1 |
50 |
51 |
60 |
|
|
2 |
30 |
32 |
40 |
|
|
… |
|
|
|
|
Выполним построение математической модели и алгоритма решения функциональной задачи выпуска продукции.
 а) Обозначения
переменных:
а) Обозначения
переменных:
n – количество видов продукции;
m – количество месяцев;
VР(n, m) – массив выпуска продукции;
i – счётчик цикла, вид продукции; j – номер месяца;
S(i) – общий выпуск продукции i-того вида;
Max(i) – максимальный выпуск продукции i-того вида;
K(i)– месяц соответствующий максимальному выпуску продукции.
б) Тип переменных:
n, m, i, j – простые переменные целого типа;
VР(n, m), Max(n), S(n) – массив вещественного типа;
K(n) – массив целого типа;
VP(i, j), K(i), Max(i), S(i) – переменные с индексом;
в) Классификация по группам:
исходные данные: n, m, VР(n, m)
промежуточные результаты: i, j; результаты: S(i), K(i), Max(i).
г) Система расчетных формул:
1) нахождение общего выпуска продукции каждого вида:
-
i = 1
начальное значение вида продукции
S

 (i)
= 0
(i)
= 0обнуление суммы выпуска i-того вида продукции
j = 1
начальный номер месяца
S

 (i)
= S(i)
+ VP(i,
j)
(i)
= S(i)
+ VP(i,
j)накопление суммы в цикле
j = j + 1
следующее значение номера месяца
Е сли
j≤m,
то
повторять действия, иначе
выход из цикла
сли
j≤m,
то
повторять действия, иначе
выход из цикла

-
i = i + 1
следующее значение вида продукции
Е
 сли
i≤n,
то
повторять действия, иначе
выход из цикла
сли
i≤n,
то
повторять действия, иначе
выход из цикла
2) нахождение максимального выпуска продукции каждого вида и месяца с максимальным выпуском:
-
i = 1
начальное значение вида продукции
M

 ax(i)
= VP(i,
1)
ax(i)
= VP(i,
1)за начальное значение максимума выбираем выпуск i-той продукции за 1-ый месяц
K(i) = 1
начальный номер месяца
j = 2
начальный номер следующего элемента
Е

 сли
VP(i, j)>Max(i), то
Max(i)
= VP(i, j); K(i) = j
сли
VP(i, j)>Max(i), то
Max(i)
= VP(i, j); K(i) = jформирование нового максимума и его номера
j = j + 1
следующее значение номера месяца
Е сли
j≤m,
то
повторять действия, иначе
выход из цикла
сли
j≤m,
то
повторять действия, иначе
выход из цикла

-
i = i + 1
следующее значение вида продукции
Е сли
i≤n,
то
повторять действия, иначе
выход из цикла
сли
i≤n,
то
повторять действия, иначе
выход из цикла

Представим алгоритм нахождения общего выпуска продукции каждого вида в виде блок-схемы (рис.19):
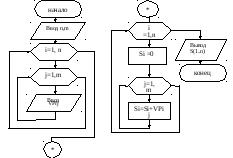 Рис.
19 Блок-схема алгоритма к примеру 10-1)
Рис.
19 Блок-схема алгоритма к примеру 10-1)
Представим алгоритм нахождения максимального выпуска продукции каждого вида в виде блок-схемы (рис.20):
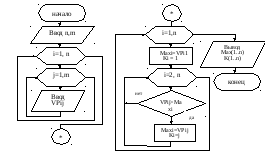
Рис. 20 Блок-схема алгоритма к примеру 10-2)
Примечание. В блок-схемах (рис. 19, рис. 20) приведён укрупнённый цикл вывода массива в виде одного блока.
