
- •Содержание
- •1. Алгоритмы решения вспомогательных задач
- •1.1 Нахождение корня уравнения
- •1.2 Вычисление коэффициентов Фурье
- •1.3 Вычисление тригонометрического полинома и построение графиков функции.
- •1.4 Построение графика спектра амплитуд сигнала
- •2. Общий листинг программы в Delphi
- •Список литературы
1.2 Вычисление коэффициентов Фурье
Тригонометрическим рядом Фурье функции
 называется функциональный ряд вида
называется функциональный ряд вида
 ,
где
,
где


 – коэффициенты Фурье функции
– коэффициенты Фурье функции

Если рассматривать отсчёты
 как значение некоторой функции
как значение некоторой функции
 ,
то заданной на равномерной сетке узлов
,
то заданной на равномерной сетке узлов
 отрезка [0,T], T=
отрезка [0,T], T= ,
то вычисление коэффициентов Фурье можно
выполнять по формулам, которые получаются
из формул приведенных выше применением
квадратурных формул правых либо левых
прямоугольников с N узлами
,
то вычисление коэффициентов Фурье можно
выполнять по формулам, которые получаются
из формул приведенных выше применением
квадратурных формул правых либо левых
прямоугольников с N узлами



Коэффициенты тригонометрического полинома зависят только от величины отсчетов сигнала и, в незначительной степени, от числа узлов разбиения сетки , при увеличении которого уменьшаются погрешности квадратурной формулы и коэффициенты полинома приближаются к соответствующим коэффициентам ряда Фурье
Вычисление коэффициентов Фурье реализуем в процедуре Trig, которая вызывается в процедуре Button2Click
Процедура Trig (блок-схема №3)
Входные переменные:
m – число коэффициентов;
n – количество узлов;
y – массив значений заданной функции в узлах сетки.
Выходные переменные:
a,b,a0 – коэффициенты Фурье.
Массив Y формируется в процедуре Button2Click до вызова процедуры Trig.
1.3 Вычисление тригонометрического полинома и построение графиков функции.
Конечная сумма Фурье соответствующая заданной функции, имеет вид

Для очередного x находим
сумму ряда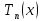 изменяя
изменяя
 от 1..m, где m
– число коэффициентов.
от 1..m, где m
– число коэффициентов.
Построение графиков выполним в интервале
 [ –T;T].
[ –T;T].
 изменяем на
изменяем на
 .
Чем меньше
.
Чем меньше
 тем точнее построение графика. Так как
значения
тем точнее построение графика. Так как
значения
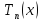 и заданного сигнала, величины вещественные
то для вывода графика необходим ввод
масштабного коэффициента
и заданного сигнала, величины вещественные
то для вывода графика необходим ввод
масштабного коэффициента
 .
.
Вывод графиков осуществим при помощи
компонента Delphi – Chart.
Для корректного отображения значений
по оси
 ,необходимо
сформированные значения компонентом
Chart поделить на коэффициент
,необходимо
сформированные значения компонентом
Chart поделить на коэффициент

Вычисление
 и построение его графика и графика
заданного сигнала реализуем в процедуре
Button3Click (блок-схема №4).
и построение его графика и графика
заданного сигнала реализуем в процедуре
Button3Click (блок-схема №4).
Процедура Button3Click.
Т – корень полинома, интервал построения графиков
sumTn – конечная сумма
ряда Фурье рассчитанная по формуле

Tn – суммирование SumTn по k=1..m
my – локальная константа, коэффициент масштабирования для графиков
dx – шаг изменения x
S – значение заданного сигнала в x
TnV – Tn с примененным масштабным коэффициентом
Sv – S с примененным масштабным коэффициентом
xV – x с примененным масштабным коэффициентом
1.4 Построение графика спектра амплитуд сигнала
Амплитуда A сигнала рассчитывается по формуле
 ,
где
,
где
 коэффициенты
Фурье, k=1..m
коэффициенты
Фурье, k=1..m
Построение спектра амплитуд сигнала реализуем в процедуре Button4.click (блок-схема №5).
Процедура Button4.click
Amp – массив размерности m, массив амплитуд сигнала
a,b - коэффициенты Фурье.
2. Общий листинг программы в Delphi
unit spectr;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, Buttons, ExtCtrls;
type
TForm1 = class(TForm)
Button1: TButton;
Button2: TButton;
Button3: TButton;
Button4: TButton;
Label1: TLabel;
Label2: TLabel;
Label3: TLabel;
ListBox1: TListBox;
Label4: TLabel;
Edit1: TEdit;
Label5: TLabel;
BitBtn1: TBitBtn;
BitBtn2: TBitBtn;
Image1: TImage;
ListBox2: TListBox;
Label6: TLabel;
Label7: TLabel;
Label8: TLabel;
Button5: TButton;
procedure Button1Click(Sender: TObject);
procedure Button2Click(Sender: TObject);
procedure Button3Click(Sender: TObject);
procedure Button4Click(Sender: TObject);
procedure Edit1KeyPress(Sender: TObject; var Key: Char);
procedure BitBtn1Click(Sender: TObject);
procedure Button5Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
{ = все процедуры и объявления глобальных переменных размещаем здесь}
const
N=80; {число узлов дискретизации}
m=N div 2;{число коэффициентов}
x0=0;
T=3;{период сигнала}
hx=T/N;
type
koeff=array[0..m] of real;
dann=array[0..N] of real;
var
Y:dann;
a,b:koeff;
Tau:real; {корень полинома = длительность сигнала}
h:real;{шаг поиска интервала расположения корня}
eps:real;{точность поиска корня}
La:real;{левый конец интервала расположения корня}
Rb:real; {правый конец интервала расположения корня}
Nkoeff:integer;{число коэффициентов полинома}
{фунция, задающая вычисление полинома в точке}
function polynom(t:real):real;
begin
polynom:=sqr(sqr(t))*t-7*t-14;
end;
function Interval(a:real):real;
var
yleft,y,x:real;
cod:integer;
begin
val(Inputbox('шаг поиска','например 0.2','1.7'),h,cod);
yleft:=polynom(a);
x:=a;
repeat
y:=polynom(x);
x:=x+h;
until y*yleft<0;
Interval:=x-h;
end;
{процедуры метода простой итерации}
function derive(x:real):real;
begin
derive:=5*sqr(sqr(x))-7;
end;
function max_derive(a,b:real):real;
const
h=0.01;
var
p,q,x:real;
begin
p:=derive(a);
x:=a;
while x<b do
begin
q:=derive(x);
if abs(p)< abs(q) then
p:=q;
x:=x+h;
end;
max_derive:=p;
end;
procedure correct(var eps:real);
const
eps0=0.00001;{погрешность определения корня}
var
Num:real;
posx,posy:integer;
begin
form1.Label5.Width:=230;
form1.Label5.Caption:='Если нужно изменить точность поиска корня'
+' то нажмите Yes и измените значение в окне Edit,'
+' либо согласитсь с предложенным вариантом и нажмите Cancel';
with form1.Edit1 do
begin
Visible:=true;
text:=floattostrF (eps0, ffFixed, 12, 7);;
posx:=Form1.ListBox1.top;
posy:=Form1.ListBox1.top;
Num:=MessageDlgPos('eps=???',mtInformation,[mbYes,mbCancel],0,posx,posy);
if Num=2 then
eps:=Strtofloat(Form1.Edit1.text)
else
begin
eps:=0;
form1.Edit1.SetFocus;
form1.Button2.Enabled:=false;
form1.Button1.Visible:=false;
end;
end;
end;
procedure Iter(a,b:real;var root:real;var K:integer);
const
Q0=1.99; {нормирующий множитель для ламбда}
var
lambda:real;
g:real;
x,x0:real;
Q:real;
begin
g:=max_derive(a,b);
form1.label3.caption:='max производной = '+ floattostrF(g, ffGeneral,5,1);
form1.Label5.caption:='Точность поиска корня='+floattostrF(eps,ffFixed,15,10);
lambda:=Q0/g;
x:=(a+b)/2;
k:=0;
repeat
x0:=x;
x:=x0-lambda*polynom(x0);
form1. listbox1.Items.Add(floattostrF(x,ffGeneral, 12, 9));
k:=k+1;
until abs(x-x0)<=eps;
root:=x;
end;
function signal(t:real):real;
var
z:real;
begin
if t<0 then
z:=0
else
if t<=1/2 then
z:=1
else
if t<=1 then
z:=2-2*t
else z:=0;
signal:=z;
end;
{процедура вычисления коэффициентов Фурье}
procedure Trig(m,N:integer;Y:dann;var a,b:koeff);
var
j,k:integer;
p,q:real;
x:real;
h:real;
begin
h:=2*Pi/N;
for k:=0 to m do
begin
p:=0;q:=0;
for j:=1 to N do
begin
x:=j*h;
p:=p+Y[j]*cos(x*k);
q:=q+Y[j]*sin(x*k);
end;
a[k]:=p*2/N;
b[k]:=q*2/N;
end;
end;
{===========================================================}
function Tpol(m:integer;x:real):real;
var
z:real;
k:integer;
begin
z:=a[0]/2;
for k:=1 to m do
z:=z+(a[k]*cos(k*2*Pi/T*x)+b[k]*sin(k*2*Pi/T*x));
Tpol:=z;
end;
{===========================================================}
procedure grafik(numvar:integer);
type
dann= array[0..N] of real;
var
L,R,W,H: integer;
X: dann;
Y: dann;
k:integer;
ymin,ymax:real;
Mx,My:real;
x0,y0: integer;
posx,posy:integer;
Nkf:string;
tx:real;
ypol:real;
procedure min_max(N:integer;Y:dann; var min, max:real);
var
k: integer;
begin
min:=Y[0];max:=Y[0];
for k := 1 to N do
if Y[k]> max then
max:=Y[k]
else if Y[k]< min then
min:=Y[k];
{увеличим диапазон}
max:=max+0.1;
min:=min-0.1;
end;
begin
L:=20;
R:=form1.image1.clientHeight-20;
W:=form1.image1.Width-50;
H:=form1.image1.clientheight-50;
case numvar of
1: begin
for k:=0 to N do
X[k]:=signal(hx*k/Tau);
min_max(N,X,ymin,ymax);
Mx:=W/N;
My:=H/(ymax-ymin);
x0:=L;
y0:=R-abs(Round(ymin*My));
with form1.image1.Canvas do
begin
pen.Color:=clblue;
font.Name:='Tahoma';
font.Size:=8;
font.Color:=claqua;
for k:=0 to N do
begin
posx:=x0+round(k*Mx);
posy:=y0-round(X[k]*My);
textout(posx-2,posy-8,'o');
Pixels[posx,posy]:=clRed;
end;
pen.Width:=2;
Moveto(L,R);lineto(L,R-H);
moveto(x0,y0);lineto(x0+W,y0);
font.Color:=clred;
textout(x0+W,y0+10,'x');
textout(x0+W,y0-20,floattostrF(T,ffFixed,3,0));
textout(x0+round(W*Tau/T), y0-20,'tau='+ floattostrF (Tau,ffFixed, 6, 3));
Nkf:=Inputbox('Число коэффициентов полинома','например 10','20');
Nkoeff:=strtoint(Nkf);
pen.Color:=clNavy;
tx:=0;
ypol:=Tpol(Nkoeff,tx/Tau);
posx:=x0+round(0*Mx/2);
posy:=y0-round(ypol*My);
moveto(posx,posy);
for k:=1 to 2*N do
begin
tx:=hx*k/2;
ypol:=Tpol(Nkoeff,tx/Tau);
posx:=x0+round(k*Mx/2);
posy:=y0-round(ypol*My);
lineto(posx,posy);
end;
end;
end;
2: begin
for k:=0 to m do
Y[k]:=sqrt(sqr(a[k])+sqr(b[k]));
min_max(m,Y,ymin,ymax);
Mx:=W/m;
My:=H/(ymax-ymin);
x0:=L;
y0:=R-abs(Round(ymin*My));
with form1.image1.Canvas do
begin
pen.Width:=2;
pen.Color:=clred;
Moveto(L,R);lineto(L,R-H);
moveto(x0,y0);lineto(x0+W,y0);
pen.Width:=6;
pen.Color:=clblue;
for k:=0 to m do
begin
posx:=x0+round(k*Mx);
posy:=y0-round(Y[k]*My);
moveto(posx,y0);
lineto(posx,posy);
end;
end;
end;
end;
end;
procedure TForm1.Button1Click(Sender: TObject);
var
a:real; {левый конец интервала расположения корня}
b:real; {правый конец интервала расположения корня}
begin
Form1.Caption:='Вычисляем корень полинома';
b:=Interval(0);
a:=b-h;
Label2.Caption:='корень расположен на отрезке ['+floattostr(a)+';'+floattostr(b)+']';
{коррекция точности решения уравнения}
correct(eps);
Button1.Visible:=false;
bitbtn1.Visible:=true;
La:=a;Rb:=b;
Listbox2.Visible:=false
end;
procedure TForm1.Button2Click(Sender: TObject);
var
j:integer;
s1,s2,s3:string;
{ hx:real;}
begin
Form1.Caption:='Вычисляем коэффициенты Фурье';
label2.Visible:=false;
label3.Visible:=false;
label4.Visible:=false;
label5.Visible:=false;
Edit1.Visible:=false;
Listbox1.Visible:=false;
Listbox2.Visible:=true;
Listbox2.Clear;
{ hx:=T/N;}
{здесь поместим алгоритм вычисления коэффициентов Фурье}
for j:=0 to N do
Y[j]:=signal(x0+j*hx);
Y[N]:=(Y[0]+Y[N])/2;
Trig(m,N,Y,a,b);
for j:=0 to m do
begin
str(j:2,s1);
str(a[j]:10:5,s2);
str(b[j]:10:5,s3);
listbox2.Items.Add(s1+s2+s3);
end;
Label6.Caption:='Вычислены коэффициенты Фурье';
label1.Visible:=false;
Button2.Visible:=false;
Button3.Visible:=true;
end;
procedure TForm1.Button3Click(Sender: TObject);
begin
Form1.Caption:='Построение графиков';
{здесь поместим алгоритм построения графика сигнала и триг. полинома}
Label7.Caption:='grafik signala i polinoma';
Button3.Visible:=false;
Button4.Visible:=true;
Label2.Visible:=false;
Label3.Visible:=false;
Label4.Visible:=false;
Label6.Visible:=false;
listbox1.Visible:=false;
listbox2.Visible:=false;
grafik(1);
end;
procedure TForm1.Button4Click(Sender: TObject);
begin
Form1.Caption:='Спектр амплитуд';
{здесь поместим алгоритм построения спектра амплитуд}
Label7.Caption:='Grafik spektra amplitud';
Button4.Visible:=false;
form1.image1.Canvas.FillRect(rect(0,0,clientwidth,clientheight));
grafik(2);
end;
procedure TForm1.Edit1KeyPress(Sender: TObject; var Key: Char);
begin
case key of
'0'..'9',chr(8): ;
'.' : if pos('.',Edit1.text)<>0
then key:=chr(0);
chr(13) :begin
eps:=Strtofloat(Form1.Edit1.text);
form1.BitBtn1.Visible:=true;
end;
else
key:=chr(0);
end;
end;
procedure TForm1.BitBtn1Click(Sender: TObject);
var
Kiter:integer;
begin
Iter(La,Rb,Tau,Kiter);{вызов процедуры метода итераций}
Label1.Caption:='корень равен '+floattostrF(Tau,ffFixed,15,2);
Button2.Visible:=true;
Label4.Caption:='число итераций '+inttostr(Kiter);
form1.Button2.Enabled:=true;
form1.BitBtn1.Visible:=false;
Bitbtn2.Visible:=true;
Listbox2.Visible:=false
end;
procedure TForm1.Button5Click(Sender: TObject);
begin
form1.Close
end;
end.
3. Результаты расчетов
3.1 Расчет корня полинома

Максимум производной = 661.17;
Число итераций = 159;
Точность поиска корня = 0,00001;
Корень равен = 1.94;
Корень расположен на отрезке [1.7.3.4].
3.2 Расчет коэффициентов Фурье

Всего коэффициентов = 50.
Приложение №1. Блок-схемы
Блок-схема №1 (функция Max_derive)

Блок-схема №2 (процедура Iter)

Блок-схема №3 (процедура Trig)


Блок-схема №4 (процедура Button3Click)


Блок-схема №5 (процедура Button4.click)

Приложение №2. Графическая часть работы
Стартовое окно программы


На представленной форме вводиться шаг вычисляемого полинома

После ввода всех необходимых параметров производиться расчет корня искомого полинома с точностью 0,00001 на отрезке [0…1.7] (значения являются значениями по умолчанию, но есть возможность их изменить)
На данном шаге производится вычисление коэффициентов Фурье при N=100, для определения смещения сигнала
График сигнала и полинома при N=100

График спектра амплитуд при N=100

