
- •Введение
- •1.Частные случаи задач
- •1.1. Задача №1
- •1.2. Задача №2
- •1.3. Задача №3
- •1.4. Задача №4
- •1.5. Выводы
- •2. Выполнение задания
- •2.1. Задача по построению линии пересечения плоскостей
- •2.2 Построение ортогональной проекции треугольника на плоскость параллелограмма
- •2.3. Построение плоскости, параллельной плоскости параллелограмма
- •2.4. Построение натуральной величины высоты параллелограмма
- •Заключение
2. Выполнение задания
2.1. Задача по построению линии пересечения плоскостей
Для решения этой задачи преобразуем плоскость параллелограмма в проецирующую. Для этого проведем в параллелограмме главную линию – горизонталь или фронталь. Выбор линии определяется заданным чертежом и наличием вокруг него свободного пространства. В примере удобно построить горизонталь.
Выбираем ось проекций Х перпендикулярно главной линии параллелограмма ( в примере – горизонтали). Получили новую систему плоскостей проекций П1-П4.
Строим в системе П1-П4 параллелограмм и треугольник, используя для этого координаты Z точек. Если построения проведены верно, то параллелограмм спроецируется в прямую на плоскость П4. Далее проводим решение задачи в частном виде в системе плоскостей проекций П1-П4.
Для того чтобы вернуться к исходному чертежу, надо найти проекции точек по принадлежности их сторонам треугольника. Пример решения задачи показан на рисунке 6.
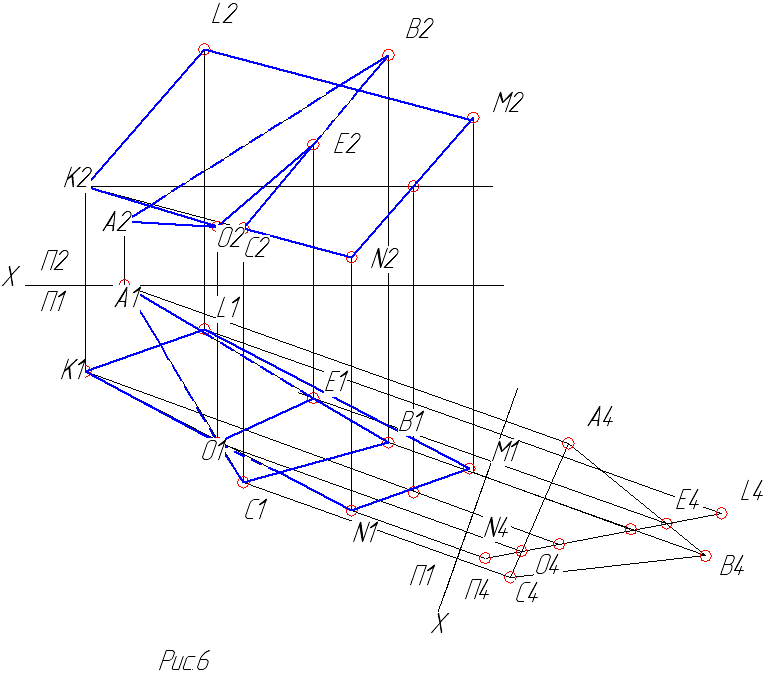
2.2 Построение ортогональной проекции треугольника на плоскость параллелограмма
Для решения этой задачи преобразуем плоскость параллелограмма в проецирующую, т.е. выполним построение, проведенное в предыдущей задаче. Следовательно, решение этой задачи можно рассматривать, как продолжение предыдущей (смотри рис.6).
Продолжим решение на рис.6. Для нахождения ортогональной проекции треугольника на плоскость параллелограмма найдем ортогональную проекцию каждой вершины треугольника на параллелограмм. Для этого проведем из вершин треугольника перпендикуляры на плоскость параллелограмма в системе плоскостей проекций П1-П4. Точка пересечения перпендикуляров с прямой, в которую проецируется параллелограмм, и есть ортогональная проекция вершин на плоскость параллелограмма.
Эти перпендикуляры являются прямыми уровня, следовательно на плоскость проекций П1 они проецируются в прямые, параллельные оси Х (П1-П4). Из этого условия находим горизонтальную проекцию ортогональных проекций.
Фронтальную проекцию найдем по линиям связи, откладывая от оси Х (П1-П2) расстояние от соответствующих проекций до оси Х (П1-П4).
Все построения приведены на рисунке 7.

2.3. Построение плоскости, параллельной плоскости параллелограмма
В задаче №3 надо построить плоскость треугольника, параллельную плоскости параллелограмма на расстоянии 40 мм.
Для решения задачи преобразуем плоскость параллелограмма в проецирующую. Для этого выберем новую ось проекций ( П1-П4) перпендикулярно горизонтали параллелограмма, как это было сделано в предыдущих задачах. В этой задаче работаем только с параллелограммом.
Сначала найдем точку, удаленную от параллелограмма на расстоянии 40 мм. Для этого восстановим перпендикуляр длиною 40 мм из одной из вершин параллелограмма, например из К ( построение проведем в системе плоскостей проекции П1-П4). Получим проекцию точки, расположенной от параллелограмма на расстоянии 40 мм – R4.
Так как перпендикуляр есть отрезок уровня, то на плоскость проекций П1 он спроецируется параллельно оси Х (П1-П4). Из этого условия найдем проекцию точки R (R1).
Затем найдем проекцию R2 из условия, что она отстоит от оси Х (П1-П2) на том же расстоянии, что R4 от оси Х (П1-П4).
Все эти построения приведены на рисунке 8.

