Титул

Задание

1. Построить интерполяционный многочлен методом неопределенных коэффициентов.

2. Построить график интерполяционной функции.

3. Найти приближенные значения функции при данных промежуточных значениях аргумента.

4. Найти приближенные значения функции при данных промежуточных значениях аргумента с помощью кубического сплайна и визуализируйте результаты сплайн-интерполяции.

7
x	y
1,340	4,2556
1,345	4,3532
1,350	4,4552
1,355	4,5618
1,360	4,6734
1,365	4,7903
1,370	4,9130
1,375	5,0419
1,380	5,1774
1,385	5,3201
1,390	5,4706
в точке x=1,3921

Решение

1. Создаем файл Pol.m, содержащий описание функции, возвращающей значения полинома .

function z=Pol(a,x1)

M1=length(a);

s=0;

for i=1:M1

s=s+a(i)*x1.^(M1-i);

end;

z=s;

Создаем файл Vandermond.m, содержащий описание функции, возвращающей значения элементов матрицы Вандермонда.

function z=Vandermond(x)

N=length(x);

z=ones(N,N);

for i=1:N

for j=1:N

z(i,j)=x(i).^(N-j);

end;

end;

Задаем значения экспериментальных данных.

>> x=[1.340;1.345;1.350;1.355;1.360;1.365;1.370;1.375;1.380;1.385;1.390]

x =

1.3400

1.3450

1.3500

1.3550

1.3600

1.3650

1.3700

1.3750

1.3800

1.3850

1.3900

>> y=[4.2556;4.3532;4.4552;4.5618;4.6734;4.7903;4.9130;5.0419;5.1774;5.3201;5.4706]

y =

4.2556

4.3532

4.4552

4.5618

4.6734

4.7903

4.9130

5.0419

5.1774

5.3201

5.4706

Вычисляем значения элементов матрицы Вандермонда.

>> M=Vandermond(x)

M =

18.6659 13.9297 10.3953 7.7577 5.7893 4.3204 3.2242 2.4061 1.7956 1.3400

19.3742 14.4046 10.7097 7.9626 5.9202 4.4016 3.2726 2.4331 1.8090 1.3450

20.1066 14.8937 11.0324 8.1722 6.0534 4.4840 3.3215 2.4604 1.8225 1.3500

20.8638 15.3976 11.3636 8.3864 6.1892 4.5677 3.3710 2.4878 1.8360 1.3550

21.6466 15.9166 11.7034 8.6054 6.3275 4.6526 3.4210 2.5155 1.8496 1.3600

22.4557 16.4511 12.0521 8.8293 6.4684 4.7387 3.4716 2.5433 1.8632 1.3650

23.2919 17.0014 12.4098 9.0582 6.6119 4.8262 3.5228 2.5714 1.8769 1.3700

24.1561 17.5681 12.7768 9.2922 6.7580 4.9149 3.5745 2.5996 1.8906 1.3750

25.0490 18.1515 13.1532 9.5313 6.9068 5.0049 3.6267 2.6281 1.9044 1.3800

25.9715 18.7520 13.5394 9.7757 7.0583 5.0962 3.6796 2.6567 1.9182 1.3850

26.9245 19.3702 13.9354 10.0254 7.2125 5.1889 3.7330 2.6856 1.9321 1.3900

Column 11

1.0000

1.0000

1.0000

1.0000

1.0000

1.0000

1.0000

1.0000

1.0000

1.0000

1.0000

Вычисляем значения коэффициентов полинома.

>> a=M^-1*y

Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND =

2.020637e-019.

a =

1.0e+010 *

0.0482

-0.4002

1.2414

-1.3953

-1.0762

4.1044

-1.9139

-4.7780

7.7122

-4.5445

1.0020

Таким образом, полином имеет вид:

P₁₀ = (0,0482*x¹⁰ – 0.4002*x⁹ + 1.2414*x⁸ – 1.3953*x⁷ – 1,0762*x⁶ + 4,1044*x⁵ – – 1,9139*x⁴ – 4,7780*x³ + 7,7122*x² – 4,5445*x + 1,0020)*10¹⁰

2. Построим график

>> x1=1.335:0.001:1.395;

>> y1=Pol(a,x1);

>> plot(x1,y1)

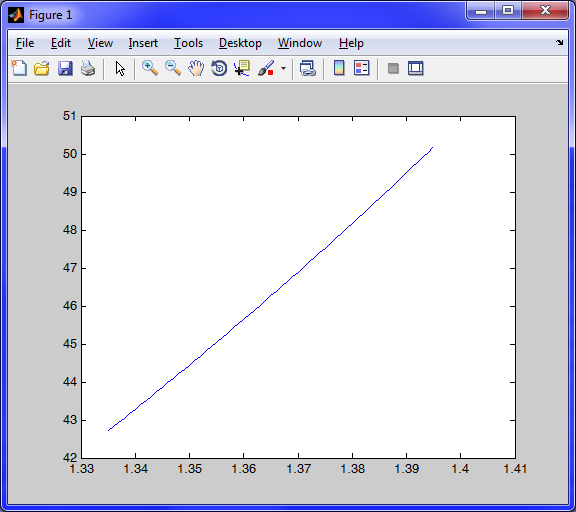
3. Вычислить значение полинома в заданной промежуточной точке х=1,3921.

>> x1=1.3921;

>> y1=Pol(a,x1)

y1 =

49.7904

4. Найдем приближенное значение функции с помощью кубического сплайна:

>> xi=1.3921;

>> yi=spline(x,y,xi)

yi =

5.5363

Визуализируем результаты сплайн-интерполяции:

>> xi=1.335:0.001:1.395;

>> yi=spline(x,y,xi);

>> plot(xi,yi)