Титул

Задание

1. Решить СЛАУ методом Гаусса с точностью 0,001.

2. Решить СЛАУ методом простой итерации с точностью 0,001.

3. Решить СЛАУ методом Зейделя с точностью 0,001.

4. Провести сравнительную характеристику методов.

5. Решить СЛАУ в системе MATLAB с помощью встроенной функции.

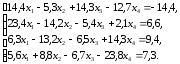
Решение

1. Создаем файл perest.m, содержащий описание функции, осуществляющей перестановку строк при обнаружении в текущей строке нулевого элемента на главной диагонали.

function z=perest(C,i)

k=i+1;

while C(k,i)==0

k=k+1;

end;

for j=1:size(C,1)

s=C(i,j);

C(i,j)=C(k,j);

C(k,j)=s;

end;

z=C;

Создаем файл diag_mat.m, содержащий описание функции, приводящий расширенную матрицу системы к диагональному виду.

function z=diag_mat(A,b)

N=size(A,1); % Определение числа уравнений системы

C=cat(2,A,b); % Создание расширенной матрицы системы

for i=1:N-1

if C(i,i)==0

C=perest(C,i);

end;

for j=0:N

C(i,N+1-j)=C(i,N+1-j)/C(i,i);

end;

for m=i+1:N

t=C(m,i);

for j=i:N+1

C(m,j)=C(m,j)-t*C(i,j);

end;

end;

end;

C(N,N+1)=C(N,N+1)/C(N,N);

C(N,N)=1;

z=C;

Создаем файл Gauss.m, содержащий описание функции, возвращающей решение системы линейных уравнений методом Гаусса.

function z=Gauss(A,b)

C=diag_mat(A,b);

N=size(A,1);

v(N)=C(N,N+1);

for j=1:N-1

s=0;

for k=0:j-1

s=s+C(N-j,N-k)*v(N-k);

end;

v(N-j)=(C(N-j,N+1)-s)/C(N-j,N-j);

end;

z=v';

Задаем матрицу системы линейных уравнений:

>> A=[14.4, -5.3 14.3 -12.7; 23.4 -14.2 -5.4 2.1; 6.3 -13.2 -6.5 14.3; 5.6 8.8 -6.7 -23.8]

A =

14.4000 -5.3000 14.3000 -12.7000

23.4000 -14.2000 -5.4000 2.1000

6.3000 -13.2000 -6.5000 14.3000

5.6000 8.8000 -6.7000 -23.8000

Задаем вектор-столбец свободных членов:

>> b=[-14.4; 6.6; 9.4; 7.3]

b =

-14.4000

6.6000

9.4000

7.3000

Решаем систему уравнений, использую функцию Gauss( ):

>> x=Gauss(A,b)

x =

-0.3269

-0.6066

-1.1540

-0.2831

Проверяем правильность решения системы линейных уравнений:

>> A*x-b

ans =

1.0e-014 *

0.1776

0

0.3553

-0.6217

Решением системы методом Гаусса является вектор-столбец .

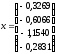2. Для начала преобразуем данную систему к виду пригодному для итерационного процесса:

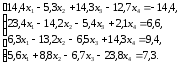
Возьмем первым уравнением второе, вторым – сумма второго и удвоенного третьего уравнения, третьим – разницу первого и четвертого, а четвертым – четвертое уравнение:

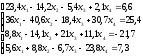
Разделим каждое уравнение на диагональный коэффициент и выразим из каждого уравнения диагональное неизвестное:

Создаем файл Iterac.m, содержащий описание функции, возвращающей решение системы линейных уравнений методом простой итерации.

function Iterac(C1,d1,eps)

N=size(C1,1);

R1=d1;

q1=R1;

q2=(C1*q1)+R1;

p=0;

s=0;

for i=1:N

if abs(q2(i)-q1(i))>s

s=abs(q2(i)-q1(i));

end;

end;

while s>eps

p=p+1;

q1=q2;

q2=(C1*q1)+R1;

s=0;

for i=1:N

if abs(q2(i)-q1(i))>s

s=abs(q2(i)-q1(i));

end;

end;

end;

q2

(C1*q2)+R1-q2

p

abs(q2-q1)

Задаем матрицу системы, приведенной к виду, пригодному для метода простой итерации:

>> A=[0 0.6068 0.2308 -0.0897; 0.8867 0 -0.4532 0.7562; -0.4190 0.6714 0 -0.5286; 0.2353 0.3697 -0.2815 0]

A =

0 0.6068 0.2308 -0.0897

0.8867 0 -0.4532 0.7562

-0.4190 0.6714 0 -0.5286

0.2353 0.3697 -0.2815 0

Задаем вектор-столбец свободных членов:

>> b=[0.2821; -0.6256; -1.0333; -0.3067]

b =

0.2821

-0.6256

-1.0333

-0.3067

Найдем решение системы линейных уравнений:

>> Iterac(A,b,0.001)

q2 =

-0.3200

-0.5959

-1.1525

-0.2774

ans =

1.0e-003 *

-0.5843

-0.9052

-0.1195

-0.4800

p =

37

ans =

1.0e-003 *

0.6396

0.9909

0.1308

0.5254

Решением системы является вектор-столбец 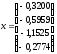, полученный на 37 шаге итерации.

3. Создаем файл Zeidel.m, содержащий описание функции, выполняющей последовательно: а) приведение системы к нормальному виду; б) приведение нормальной системы к виду, пригодному для итерационного процесса Зейделя; в) реализацию итерационного процесса Зейделя.

function Zeidel(A,b,eps);

N=size(A,1);

% Приведение системы к нормальному виду

C=A'*A;

D=A'*b;

% Приведение системы к виду, пригодному для итерационного процесса

for i=1:N

D1(i)=D(i)/C(i,i);

end;

D1=D1'; % Транспонирование матрицы

d1=D1;

for i=1:N

for j=1:N

if i==j

C1(i,j)=0;

else

C1(i,j)=-C(i,j)/C(i,i);

end;

end;

end;

% Решение СЛАУ методом Зейделя

R1=d1;

q1=R1;

% Создание матрицы для хранения промежуточных данных

t=size(C1);

N=t(1,1);

q2=zeros(t(1,1),1);

% Цикл вычислений

p=0;

s=0;

for i=1:N

if abs(q2(i)-q1(i))>s

s=abs(q2(i)-q1(i));

end;

end;

while s>eps

q2=q1;

p=p+1;

for f=1:N

v=(C1*q1)+R1;

x(f,1)=v(f,1);

q1(f,1)=x(f,1);

end;

s=0;

for i=1:N

if abs(q2(i)-q1(i))>s

s=abs(q2(i)-q1(i));

end;

end;

q1=x;

end;

'Ответы:'

q2

'Проверка:'

A*q2

'число проходов:'

p

abs(q2-q1)

Задаем значения коэффициентов при неизвестных исходной системы линейных уравнений и столбец свободных членов:

>> A=[14.4 -5.3 14.3 -12.7; 23.4 -14.2 -5.4 2.1; 6.3 -13.2 -6.5 14.3; 5.6 8.8 -6.7 -23.8];

>> b=[-14.4; 6.6; 9.4; 7.3];

Вычислием решение системы линейных уравнений, используя функцию Zeidel():

>> Zeidel(A,b,0.001)

ans =

Ответы:

q2 =

-0.2882

-0.5479

-1.1468

-0.2522

ans =

Проверка:

ans =

-14.4433

6.6983

9.2641

7.2501

ans =

число проходов:

p =

141

ans =

1.0e-003 *

0.6556

0.9942

0.1216

0.5232

Решением системы линейных уравнений является вектор 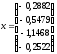, найденный на 141 шаге итерации.

4. Метод итераций обеспечивает более точный и более быстрый поиск решения.

5. Программа решения системы уравнений имеет вид:

>> syms x1 x2 x3 x4;

>> Y=solve('14.4*x1-5.3*x2+14.3*x3-12.7*x4=-14.4', '23.4*x1-14.2*x2-5.4*x3+2.1*x4=6.6', '6.3*x1-13.2*x2-6.5*x3+14.3*x4=9.4', '5.6*x1+8.8*x2-6.7*x3-23.8*x4=7.3')

Y =

x1: [1x1 sym]

x2: [1x1 sym]

x3: [1x1 sym]

x4: [1x1 sym]

>> Y.x1

ans =

-0.32693623778859110787514970327585

>> Y.x2

ans =

-0.60656826121660040341702356780641

>> Y.x3

ans =

-1.1539776394707657924312325115094

>> Y.x4

ans =

-0.28306695150706146827232722302221