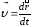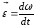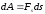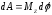- •Часть 3
- •Динамика твердого тела краткая теория
- •Определение момента инерции
- •Момент инерции сплошного цилиндра
- •Теорема Штейнера
- •Кинетическая энергия вращающегося твердого тела
- •Плоское движение твердого тела
- •Момент силы. Уравнение динамики вращательного движения твердого тела Момент силы
- •Уравнение динамики вращательного движения твердого тела
- •Момент импульса
- •Закон сохранения момента импульса
- •Некоторые демонстрации закона сохранения момента импульса
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Приложение Формулы алгебры и тригонометрии
- •Некоторые сведения о векторах
- •Рекомендуемая литература
Момент импульса
Момент
импульса материальной точки относительно
неподвижной точки
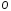 - физическая величина, определяемая
векторным произведением радиуса-вектора
- физическая величина, определяемая
векторным произведением радиуса-вектора
 материальной точки, проведенного из
точки
материальной точки, проведенного из
точки
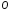 ,
на импульс
,
на импульс
 этой материальной точки
этой материальной точки
 (12)
(12)
Модуль вектора момента импульса
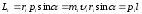 , (13)
, (13)
где
α
– угол между векторами
 и
и
 ;
;
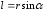 - плечо импульса. Перпендикуляр опущен
из точки
- плечо импульса. Перпендикуляр опущен
из точки
 на прямую, вдоль которой направлен
импульс частицы.
на прямую, вдоль которой направлен
импульс частицы.
Рисунок
7 – Момент импульса материальной точки
относительно неподвижной точки О

 -
осевой
вектор (псевдовектор),
его направление совпадает с направлением
поступательного движения правого винта
при его вращении от
-
осевой
вектор (псевдовектор),
его направление совпадает с направлением
поступательного движения правого винта
при его вращении от
 к
к
 .
.
Момент
импульса материальной точки относительно
неподвижной оси z
- скалярная
величина
Liz,
равная
проекции на эту
ось вектора момента
импульса, определенного относительно
произвольной точки
 данной
оси z.
данной
оси z.
Значение
момента импульса Liz
не
зависит от положения точки О
на оси z.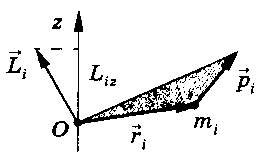
Рисунок 8 – Момент импульса материальной точки относительно неподвижной оси z
Момент импульса отдельной точки вращающегося абсолютно твердого тела
 . (14)
. (14)
При
вращении абсолютно твердого тела вокруг
неподвижной оси z
каждая
отдельная точка тела движется по
окружности постоянного радиуса
 с
некоторой скоростью
с
некоторой скоростью
 .
Скорость
.
Скорость
 и
импульс
и
импульс
 перпендикулярны этому радиусу, т. е.
радиус — плечо вектора
перпендикулярны этому радиусу, т. е.
радиус — плечо вектора
 .
Тогда
момент импульса отдельной частицы
.
Тогда
момент импульса отдельной частицы
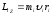 и направлен по оси в сторону, определяемую
правилом правого винта.
и направлен по оси в сторону, определяемую
правилом правого винта.
Момент импульса абсолютно твердого тела относительно неподвижной оси z - сумма моментов импульса отдельных его частиц относительно той же оси.
 , (15)
, (15)
равен произведению момента инерции тела относительно той же оси на угловую скорость
 . (16)
. (16)
Учтем,
что

 ,
,
где
 - момент
инерции тела относительно оси z,
- момент
инерции тела относительно оси z,
 – угловая скорость.
– угловая скорость.
Таблица 2 Аналогия в описании поступательного и вращательного движений
|
Поступательное движение |
Вращательное движение |
|||
|
Масса |
m |
Момент инерции |
|
|
|
Скорость |
|
Угловая скорость |
|
|
|
Ускорение |
|
Угловое ускорение |
|
|
|
Сила |
|
Момент силы |
|
|
|
Основное уравнение динамики |
|
Основное уравнение динамики |
|
|
|
Работа |
|
Работа |
|
|
|
Кинетическая энергия |
|
Кинетическая энергия |
|
|
Закон сохранения момента импульса
Еще одна форма записи уравнения динамики вращательного движения твердого тела - производная момента импульса твердого тела относительно оси равна моменту силы относительно той же оси
 . (17)
. (17)
Продифференцировав
 по времени, получим записанное выражение:
по времени, получим записанное выражение:
 . (18)
. (18)
Производная вектора момента импульса твердого тела равна моменту (сумме моментов) внешних сил
 . (19)
. (19)
Закон сохранения момента импульса:
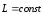 . (20)
. (20)
Момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени.
В
замкнутой системе момент внешних сил
 и
и
 ,
откуда
,
откуда
 .
.
Закон сохранения момента импульса — фундаментальный закон природы.
Закон сохранения момента импульса – следствие изотропности пространства.
Изотропность пространства - инвариантность физических законов относительно выбора направления осей координат системы отсчета (относительно поворота замкнутой системы в пространстве на любой угол).