
- •Структура модуля.
- •Знання та вміння, якими повинен володіти студент
- •1. Знання на рівні понять, означень, формулювань.
- •2. Уміння в розв’язанні задач.
- •Тема 1. Матриці та дії над ними.
- •Найпростіші дії з матрицями
- •Приклади розв’язання типових задач.
- •Самостійна робота №1
- •Тема 2. Визначник матриці. Властивості визначника.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №2
- •Самостійна робота №3
- •Тема 3. Ранг матриці. Основні теоретичні відомості
- •Приклади розв’язання типових задач.
- •Індивідуальні завдання.
- •Тема 4. Обернена матриця.
- •Матричні рівняння.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №4
- •Тема 5. Розв’язання систем лінійних алгебраїчних рівнянь.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №5
- •Тема 6. Розв’язання систем лінійних алгебраїчних рівнянь матричним методом.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №6
- •Тема 7. Розв’язання систем лінійних алгебраїчних рівнянь методом Гаусса. Основні теоретичні відомості
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №7
- •Структура модуля.
- •Знання та вміння, якими повинен володіти студент
- •1. Знання на рівні понять, означень, формулювань.
- •2. Уміння в розв’язанні задач.
- •Самостійна робота №8
- •Тема 1. Загальні поняття.
- •Тема 2. Координати вектора. Дії над векторами.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Тема 3. Скалярний добуток векторів.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №9
- •Тема 4. Векторний добуток векторів. Основні теоретичні відомості
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №10
- •Структура модуля.
- •Знання та вміння, якими повинен володіти студент
- •1. Знання на рівні понять, означень, формулювань.
- •Самостійна робота №11
- •Тема 1. Пряма лінія.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Тема 2. Загальне рівняння прямої.
- •Канонічне рівняння прямої
- •Рівняння прямої, яка проходить через дві задані точки.
- •Векторне параметричне рівняння прямої
- •Параметричні рівняння прямої
- •Рівняння прямої у відрізках на осях.
- •Рівняння прямої з кутовим коефіцієнтом
- •Відстань від точки до прямої
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №12,13,14,15.
Вправи для аудиторної роботи.
1. Розв’яжіть системи рівнянь методом Гаусса:
1)
 .
2)
.
2)
 .
.
3)
 .
4)
.
4)
 .
.
5)
 .
6)
.
6)
 .
.
Самостійна робота №7
7.1. Розв’яжіть систему лінійних рівнянь методом Гаусса:
1)
 .
2)
.
2)
 .
.
3)
 .
4)
.
4)
 .
.
5)
 .
6)
.
6)
 .
.
7)
 .
8)
.
8)
 .
.
9)
 .
10)
.
10)
 .
.
11)
 .
12)
.
12)
 .
.
13)
 .
14)
.
14)
 .
.
15)
 .
16)
.
16)

17)
 .
18)
.
18)
 .
.
19)
 .
20)
.
20)
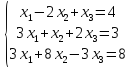 .
.
21)
 .
22)
.
22)

23)
 .
24)
.
24)
 .
.
25)
 .
.
-------------------------------------------------------------------------------------------------
Модуль 2. Елементи векторної алгебри.
Структура модуля.
Тема 1. Загальні поняття.
Тема 2. Координати вектора. Дії над векторами.
Тема 3. Скалярний добуток векторів.
Тема 4. Векторний добуток векторів.
Базисні поняття. 1. Вектор. 2. Проекція вектора. 3. Базис. 4. Декартова прямокутна система координат. 5. Координати вектора. 6. Скалярний добуток. 7. Векторний добуток. 8.Мішаний добуток.
Основні задачі. 1.Виконання операцій над векторами. 2. Вивчення взаємного розміщення векторів. 3. Застосування скалярного, векторного та мішаного добутків до розв’язання геометричних задач.
Знання та вміння, якими повинен володіти студент
1. Знання на рівні понять, означень, формулювань.
1.1. Геометричний вектор. Дії над векторами.
1.2. Лінійна залежність і незалежність векторів.
1.3. Базис на площині й у просторі.
1.4. Прямокутна декартова система координат. Координати вектора.
1.5. Скалярний добуток двох векторів.
1.6. Векторний добуток двох векторів.
1.7. Мішаний добуток двох векторів.
2. Уміння в розв’язанні задач.
2.1. Знаходити координати вектора, довжину вектора, орт вектора, кут між векторами.
2.2. Знаходити суму, різницю векторів, їх скалярний та векторний добутки.
2.3. Обчислювати площу трикутника, об’єм піраміди.
2.4. Уміти розкладати вектор за базисними векторами.
2.5.Використовувати умову перпендикулярності двох векторів.
Література: 1. Г.Я. Дутка «Практикум з математики для економістів» – Л. -1998.
2. В. П. Денисюк, В. К. Репета «Вища математика» - К. – 2005.
3. В. М. Буйвол «Елементи лінійної і векторної алгебри та аналітичної геометрії». К -1996
4. Численные методы. Учебник для техникумов. М. – 1976.
5. Н.В.Богомолов «Практические занятия по математике» . М. – 1990.
Самостійна робота №8
Тема 1. Загальні поняття.
ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ.
Векторна величина на відміну від скалярної задається не лише своїм чисельним значенням, а й напрямом (швидкість, прискорення, сила та ін.).
Геометрично вектор являє
собою напрямлений
відрізок і позначається
 ,
або
,
або
 ,
де точка А – початок вектора, а В – його
кінець.
,
де точка А – початок вектора, а В – його
кінець.


Рис.1
Відстань між початком вектора
і його кінцем називають довжиною
(або модулем)
вектора і позначають
 ,
або
,
або
 .
.
Вектори, які лежать на одній прямій або паралельних прямих, називають колінеарними.




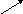



Рис.2
Вектори
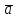 і
і
 рівні,
якщо вони колінеарні, мають однакові
модулі і однакові напрями.
рівні,
якщо вони колінеарні, мають однакові
модулі і однакові напрями.



Рис.3
Два вектори називають протилежними, якщо вони колінеарні, мають однакові модулі і протилежні напрями.




Рис.4
Вектор, початок і кінець якого збігаються, називають нуль-вектором. Напрям його не визначений.
Вектор, довжина якого дорівнює одиниці, називають одиничним вектором.
Одиничний вектор, напрям
якого збігається з напрямом вектора
 ,
називають ортом вектора
,
називають ортом вектора
 і позначають
і позначають
 .
.
Вектори можна вільно переміщувати по площині (у просторі). Тому в аналітичній геометрії їх називають вільними.
Кутом між векторами
 і
і
 ,
зведеними до спільного початку, називають
найменший кут, на який треба повернути
вектор
,
зведеними до спільного початку, називають
найменший кут, на який треба повернути
вектор
 навколо спільного початку, щоб він
збігся з вектором
навколо спільного початку, щоб він
збігся з вектором
 .
.






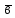




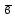






Рис.5
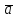

Три вектори називають компланарними, якщо вони лежать в одній або паралельних площинах.
Зокрема, три вектори компланарні, якщо два з них або всі три колінеарні, або хоча б один з них – нуль-вектор.
Лінійні операції над векторами.
До лінійних операцій над векторами належать:
1) додавання (віднімання) векторів;
2) множення вектора на число (скаляр).
Сумою
векторів
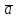 і
і
 називають вектор
називають вектор
 ,
який сполучає початок вектора
,
який сполучає початок вектора
 з кінцем вектора
з кінцем вектора
 за умови, що вектор
за умови, що вектор
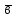 прикладений до кінця вектора
прикладений до кінця вектора
 .
.
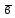


правило


трикутника
 Рис.6
Рис.6
Суму двох векторів можна будувати також за правилом паралелограма.






 Рис.7
Рис.7
Віднімання векторів визначається як дія, обернена додаванню.
Різницею
векторів
 і
і
 називають вектор
називають вектор
 ,
який у сумі з вектором
,
який у сумі з вектором
 складає вектор
складає вектор
 ,
або, іншими словами, це вектор, що сполучає
кінець вектора
,
або, іншими словами, це вектор, що сполучає
кінець вектора
 з кінцем вектора
з кінцем вектора
 за умови, що
за умови, що
 і
і
 прикладені до спільного початку.
прикладені до спільного початку.




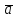


 Рис.8
Рис.8
Добутком
вектора
 на скаляр
на скаляр
 називають вектор
називають вектор
 такий, що
такий, що
 =
= і напрям якого збігається з напрямом
вектора
і напрям якого збігається з напрямом
вектора
 ,
якщо
,
якщо
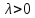 ,
або протилежний до напряму вектора
,
або протилежний до напряму вектора
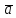 ,
якщо
,
якщо
 .
Так на рис.9 зображено вектори
.
Так на рис.9 зображено вектори
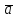 ,
4
,
4 ,
-2
,
-2 .
.
Рис.9
 4
4 -2
-2



З
означення множення вектора на число
випливає, що коли вектори колінеарні,
то існує єдине число
 таке, що
таке, що
 =
= ,
і навпаки, якщо
,
і навпаки, якщо
 =
= ,
то
,
то
 і
і
 колінеарні.
колінеарні.
Сформулюємо властивості лінійних операцій над векторами:
1.
 .
.
 .
.
 .
.
3.
 .
.
4.
 .
.
5.
 .
.
6.
 .
.
7.
 .
.
Проекція вектора на вісь.
Віссю називають напрямлену пряму, на якій вибрано початок відліку, додатний напрям і одиницю довжини.
Проекцією точки А на вісь l називають основу перпендикуляра АА1 (точка А1), опущеного з точки А на вісь l (рис.10).
 В
В
В
В 

А Рис.10 А Рис.11

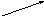
А1
 В1
l
В1
А1
l
В1
l
В1
А1
l






Нехай задано вісь l
і вектор
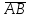 .
Позначимо через А1
та В1
проекції на вісь l
відповідно початку А і кінця В вектора
.
Позначимо через А1
та В1
проекції на вісь l
відповідно початку А і кінця В вектора
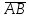 і розглянемо вектор
і розглянемо вектор
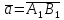 .
.
Проекцією вектора
 на вісь l називають
додатне число
на вісь l називають
додатне число
 ,
якщо вісь l
і вектор
,
якщо вісь l
і вектор
 однаково напрямлені (рис.10), і від’ємне
число
однаково напрямлені (рис.10), і від’ємне
число
 ,
якщо вісь l
і вектор
,
якщо вісь l
і вектор
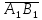 протилежно напрямлені (рис.11).
протилежно напрямлені (рис.11).
Проекцією вектора
 на вісь l
позначають так:
на вісь l
позначають так:
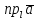 (або
(або
 ).
).
Кутом між вектором
 і віссю l називають
менший з кутів, на який треба повернути
вектор
і віссю l називають
менший з кутів, на який треба повернути
вектор
 або вісь l,
щоб він збігався за напрямом з другим
вектором або віссю. Цей кут міститься
у межах від 0 до
або вісь l,
щоб він збігався за напрямом з другим
вектором або віссю. Цей кут міститься
у межах від 0 до
 .
.
Проекцію вектора
 на вісь l
обчислюють за формулою
на вісь l
обчислюють за формулою

де
 - кут між напрямом осі l
і напрямом вектора
- кут між напрямом осі l
і напрямом вектора
 .
.
При цьому
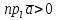 ,
якщо кут
,
якщо кут
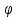 -
гострий,
-
гострий,
 ,
якщо кут
,
якщо кут
 -
тупий,
-
тупий,
 ,
якщо
,
якщо
 .
.
Сформулюємо деякі властивості проекцій.
1. Проекція суми кількох векторів на ту саму вісь дорівнює сумі їх проекцій на цю вісь, тобто
 .
.
2.
При множенні вектора
 на число
на число
 його проекція також помножиться на це
число:
його проекція також помножиться на це
число:
 .
.
Лінійна залежність і незалежність векторів. Базис.
Застосовуючи лінійні операції над векторами, можна знаходити вирази вигляду
 ,
,
Які
називають лінійними
комбінаціями векторів
 ,
,
 ,…,
,…,
 ;
числа
;
числа
 ,
,
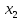 ,…,
,…,
 - коефіцієнти.
- коефіцієнти.
Вектори
 ,
,
 ,…,
,…,
 називають лінійно
залежними, якщо існують
такі числа
називають лінійно
залежними, якщо існують
такі числа
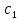 ,
,
 ,…,
,…,
 не всі рівні нулю, що лінійна комбінація
не всі рівні нулю, що лінійна комбінація
 ,
,
і
лінійно незалежними,
якщо ця рівність виконується лише за
умови, коли всі числа
 ,
,
 ,…,
,…,
 рівні нулю.
рівні нулю.
Сукупність лінійно незалежних
векторів
 ,
,
 ,…,
,…,
 називають базисом
простору
називають базисом
простору
 ,
якщо для кожного вектора з
,
якщо для кожного вектора з
 існують такі дійсні числа
існують такі дійсні числа
 ,
,
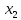 ,…,
,…,
 ,
що виконується рівність
,
що виконується рівність
 .
.
Цю
рівність називають розкладом вектора
 у базисі
у базисі
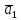 ,
,
 ,…,
,…,
 .
.
Базисом на прямій називають довільний ненульовий вектор на цій прямій.
Якщо
вектор
 - базис, то існує єдиний розклад вектора
- базис, то існує єдиний розклад вектора
 :
:
 ,
де
,
де
 - координата вектора
- координата вектора
 за базисом
за базисом
 .
.
Базисом на площині називають довільну упорядковану пару неколінеарних векторів.
Базисом у просторі називають довільну упорядковану трійку некомпланарних векторів.
Якщо вектори
 та
та
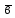 - базис на площині і
- базис на площині і
 - довільний ненульовий вектор площини,
то існують сталі
- довільний ненульовий вектор площини,
то існують сталі
 та
та
 такі, що
такі, що
 (рис.12)
(рис.12)






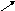



 Рис.12
Рис.12
Коефіцієнти
 ,
,
 називають координатами
вектора
називають координатами
вектора
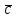 в даному базисі.
в даному базисі.
Якщо
вектори
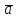 ,
,
 і
і
 - базис у просторі і вектор
- базис у просторі і вектор
 розкладений за базисом, тобто
розкладений за базисом, тобто
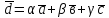 ,
то числа
,
то числа
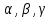 називають координатами вектора
називають координатами вектора
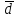 в даному базисі.
в даному базисі.
Таким чином, базис у просторі
дає змогу кожний вектор одночасно
зіставити з упорядкованою трійкою чисел
(координатами цього вектора) і, навпаки,
кожну упорядковану трійку чисел
 за допомогою базису можна зіставити з
єдиним вектором
за допомогою базису можна зіставити з
єдиним вектором
 .
.
