
- •Структура модуля.
- •Знання та вміння, якими повинен володіти студент
- •1. Знання на рівні понять, означень, формулювань.
- •2. Уміння в розв’язанні задач.
- •Тема 1. Матриці та дії над ними.
- •Найпростіші дії з матрицями
- •Приклади розв’язання типових задач.
- •Самостійна робота №1
- •Тема 2. Визначник матриці. Властивості визначника.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №2
- •Самостійна робота №3
- •Тема 3. Ранг матриці. Основні теоретичні відомості
- •Приклади розв’язання типових задач.
- •Індивідуальні завдання.
- •Тема 4. Обернена матриця.
- •Матричні рівняння.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №4
- •Тема 5. Розв’язання систем лінійних алгебраїчних рівнянь.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №5
- •Тема 6. Розв’язання систем лінійних алгебраїчних рівнянь матричним методом.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №6
- •Тема 7. Розв’язання систем лінійних алгебраїчних рівнянь методом Гаусса. Основні теоретичні відомості
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №7
- •Структура модуля.
- •Знання та вміння, якими повинен володіти студент
- •1. Знання на рівні понять, означень, формулювань.
- •2. Уміння в розв’язанні задач.
- •Самостійна робота №8
- •Тема 1. Загальні поняття.
- •Тема 2. Координати вектора. Дії над векторами.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Тема 3. Скалярний добуток векторів.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №9
- •Тема 4. Векторний добуток векторів. Основні теоретичні відомості
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №10
- •Структура модуля.
- •Знання та вміння, якими повинен володіти студент
- •1. Знання на рівні понять, означень, формулювань.
- •Самостійна робота №11
- •Тема 1. Пряма лінія.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Тема 2. Загальне рівняння прямої.
- •Канонічне рівняння прямої
- •Рівняння прямої, яка проходить через дві задані точки.
- •Векторне параметричне рівняння прямої
- •Параметричні рівняння прямої
- •Рівняння прямої у відрізках на осях.
- •Рівняння прямої з кутовим коефіцієнтом
- •Відстань від точки до прямої
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №12,13,14,15.
Вправи для аудиторної роботи.
1. Знайдіть обернені до матриць:
1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)

5)
 ;
6)
;
6)
 ;
7)
;
7)
 ;
;
8)
 ;
9)
;
9)
 ;
10)
;
10)

2.
Знайдіть матрицю
 ,
якщо:
,
якщо:
 ,
,
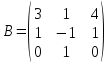 .
.
3.
Знайдіть матрицю
 ,
якщо:
,
якщо:
 .
.
Самостійна робота №4
4.1. Розв’яжіть матричні рівняння:
1)
 ,
,
 ,
,
 .
.
2)
 ,
,
 ,
,
 .
.
3)
 ,
,
 ,
,
 ,
,
 .
.
4)
 ,
,
 ,
,
 .
.
5)
 ,
,
 ,
,
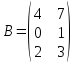 .
.
6)
 ,
,
 ,
,
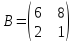 ,
,
 .
.
7)
 ,
,
 ,
,
 .
.
8)
 ,
,
 ,
,
 .
.
9)
 ,
,
 ,
,
 ,
,
 .
.
10)
 ,
,
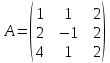 ,
,
 .
.
11)
 ,
,
 ,
,
 .
.
12)
 ,
,
 ,
,
 ,
,
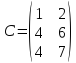 .
.
13)
 ,
,
 ,
,
 .
.
14)
 ,
,
 ,
,
 .
.
15)
 ,
,
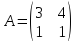 ,
,
 ,
,
 .
.
16)
 ,
,
 ,
,
 ,
,
 .
.
17)
 ,
,
 ,
,
 .
.
18)
 ,
,
 ,
,
 ,
,
 .
.
19)
 ,
,
 ,
,
 .
.
20)
 ,
,
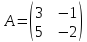 ,
,
 ,
,
 .
.
21)
 ,
,
 ,
,
 ,
,
 .
.
22)
 ,
,
 ,
,
 .
.
23)
 ,
,
 ,
,
 .
.
24)
 ,
,
 ,
,
 .
.
25)
 ,
,
 ,
,
 .
.
4.2.
Знайдіть обернену матрицю
 ,
якщо:
,
якщо:
1)
 .
2)
.
2)
 .
3)
.
3)
 .
.
4)
 .
5)
.
5)
 .
6)
.
6)
 .
.
7)
 .
8)
.
8)
 .
9)
.
9)
 .
.
10)
 .
11)
.
11)
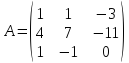 .
12)
.
12)
 .
.
13)
 .
14)
.
14)
 .
15)
.
15)
 .
.
16)
 .
17)
.
17)
 .
18)
.
18)
 .
.
19)
 .
20)
.
20)
 .
21)
.
21)
 .
.
22)
 .
23)
.
23)
 .
24)
.
24)
 .
.
25)
 .
.
----------------------------------------------------------------------------------------------------
Тема 5. Розв’язання систем лінійних алгебраїчних рівнянь.
Метод Крамера.
ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ.
Система n лінійних рівнянь з n невідомими має вигляд
 (1)
(1)
де
 ,
,
 =
= ,
,
 =
= - коефіцієнти при невідомих;
- коефіцієнти при невідомих;
 ,
,
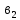 ,…,
,…, - вільні члени.
- вільні члени.
Коефіцієнти при невідомих
 ,
,
 ,…,
,…, утворюють матрицю, визначник якої
назвемо визначником
системи і позначимо
утворюють матрицю, визначник якої
назвемо визначником
системи і позначимо
 ,
,
Розв’язком системи (1) називається сукупність значень невідомих
 ,
,
 ,…,
,…, ,
які при підстановці їх у (1) перетворюють
кожне з рівнянь у рівність.
,
які при підстановці їх у (1) перетворюють
кожне з рівнянь у рівність.
Якщо система лінійних рівнянь (СЛР) має хоча б один розв’язок, то вона називається сумісною, у протилежному разі – несумісною. Якщо розв’язок системи єдиний, то СЛР називається визначеною. У разі, коли розв’язок сумісної системи не єдиний, систему рівнянь називають невизначеною.
Розв’язати систему (1) можна, користуючись правилом Крамера. Система n лінійних рівнянь з n невідомими, визначник якої не дорівнює нулю, завжди сумісна і має єдиний розв’язок, який знаходиться так: значення кожного із невідомих дорівнює дробові, знаменником якого є визначник системи, а чисельник є також визначник, який отримуємо з визначника системи заміною стовпця коефіцієнтів при шуканій змінній стовпцем вільних членів.
Таким чином, розв’язок системи (1) знаходять за формулами
 ,
,
 ,…….,
,…….,
 .
.
Матриці
 і
і

називають основною та розширеною матрицями системи (1) відповідно.
Зауваження
1. Якщо
 і
і
 (
( =
= ),
то система лінійних рівнянь має безліч
розв’язків.
),
то система лінійних рівнянь має безліч
розв’язків.
Зауваження
2. Якщо
 і хоч один із визначників
і хоч один із визначників
 (
( =
= )
не дорівнює нулю, то система лінійних
рівнянь не має розв’язків.
)
не дорівнює нулю, то система лінійних
рівнянь не має розв’язків.
