
- •Структура модуля.
- •Знання та вміння, якими повинен володіти студент
- •1. Знання на рівні понять, означень, формулювань.
- •2. Уміння в розв’язанні задач.
- •Тема 1. Матриці та дії над ними.
- •Найпростіші дії з матрицями
- •Приклади розв’язання типових задач.
- •Самостійна робота №1
- •Тема 2. Визначник матриці. Властивості визначника.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №2
- •Самостійна робота №3
- •Тема 3. Ранг матриці. Основні теоретичні відомості
- •Приклади розв’язання типових задач.
- •Індивідуальні завдання.
- •Тема 4. Обернена матриця.
- •Матричні рівняння.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №4
- •Тема 5. Розв’язання систем лінійних алгебраїчних рівнянь.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №5
- •Тема 6. Розв’язання систем лінійних алгебраїчних рівнянь матричним методом.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №6
- •Тема 7. Розв’язання систем лінійних алгебраїчних рівнянь методом Гаусса. Основні теоретичні відомості
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №7
- •Структура модуля.
- •Знання та вміння, якими повинен володіти студент
- •1. Знання на рівні понять, означень, формулювань.
- •2. Уміння в розв’язанні задач.
- •Самостійна робота №8
- •Тема 1. Загальні поняття.
- •Тема 2. Координати вектора. Дії над векторами.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Тема 3. Скалярний добуток векторів.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №9
- •Тема 4. Векторний добуток векторів. Основні теоретичні відомості
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №10
- •Структура модуля.
- •Знання та вміння, якими повинен володіти студент
- •1. Знання на рівні понять, означень, формулювань.
- •Самостійна робота №11
- •Тема 1. Пряма лінія.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Тема 2. Загальне рівняння прямої.
- •Канонічне рівняння прямої
- •Рівняння прямої, яка проходить через дві задані точки.
- •Векторне параметричне рівняння прямої
- •Параметричні рівняння прямої
- •Рівняння прямої у відрізках на осях.
- •Рівняння прямої з кутовим коефіцієнтом
- •Відстань від точки до прямої
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №12,13,14,15.
Приклади розв’язання типових задач.
Обчисліть визначники:
1.
а)
 ;
;
б)
 ;
;
в)
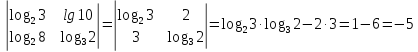 .
.
2.

Розв’язання. Перший спосіб. За правилом трикутників маємо


Другий спосіб. Використовуючи властивості визначника, дістаємо
 =
=
 =
=
 =
=
 =
=
=
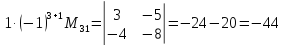 .
.
Третій спосіб. Розкладемо визначник за першим рядком:
 =
=
 +
+ +
+ =
=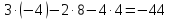 .
.
3.

Розв’язання. У визначнику є кілька нульових елементів, проте зручно, коли нульові елементи містяться в одному рядку чи стовпцеві. Зробимо, наприклад, нульовими всі елементи першого рядка, крім першого елемента. Для цього додамо до третього стовпця перший, після чого помножимо елементи першого стовпця на -2 і додамо їх до відповідних елементів четвертого стовпця. Дістанемо
 =
= =
= .
.
Тепер розкладемо визначник за елементами першого рядка:
 .
.
Занулимо два елементи другого стовпця. Для цього до першого і другого рядків по черзі додамо третій рядок. Тоді
 .
.
Розкладемо утворений визначник за елементами другого стовпця:
 .
.
Відповідь:
 .
.
4.
Розв’яжіть рівняння:
 .
.
Розв’язання. Розкладемо визначник за елементами першого рядка:
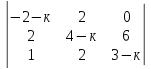 =
=
 =
= =
=
 .
.
Отже, вихідне рівняння рівносильне рівнянню

Далі маємо
 ;
;
 або
або
 ,
звідси
,
звідси
 .
.
Відповідь:
 ;
;
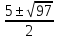 .
.
Вправи для аудиторної роботи.
Обчисліть визначники:
1.
 .
2.
.
2.
 .
3.
.
3.
 .
4.
.
4.
 .
.
5.
 .
6.
.
6.
 .
7.
.
7.
 .
8.
.
8.
 .
.
9.
 .
10.
.
10.
 .
11.
.
11.
 .
.
12.
 .
.
13.
Доведіть рівність:
 =авс(в-а)(с-а)(с-в).
=авс(в-а)(с-а)(с-в).
Відповіді: 1. 66. 2. -110. 3. 121. 4. 1. 5. 5/3. 6. 0,6. 7. 13/21. 8. -5. 9. -10. 10. -15. 11. 11. 12. 12.
Самостійна робота №2
2.1. Обчисліть визначники, використовуючи:
а) метод зведення до трикутного вигляду;
б) метод розкладу визначника за елементами деякого рядка або стовпця;
в) правило трикутників.
1)
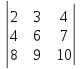 .
2)
.
2)
 .
3)
.
3)
 .
4)
.
4)
 .
.
5)
 .
6)
.
6)
 .
7)
.
7)
 .
8)
.
8)
 .
.
9)
 .
10)
.
10)
 .
11)
.
11)
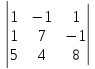 .
12)
.
12)

13)
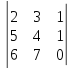 .
14)
.
14)
 .
15)
.
15)
 .
16)
.
16)
 .
.
17)
 .
18)
.
18)
 .
19)
.
19)
 .
20)
.
20)

21)
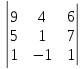 .
22)
.
22)
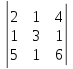 .
23)
.
23)
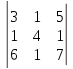 .
24)
.
24)
 .
.
25)
 .
.
2.2. Знайдіть дійсні корені рівняння:
1)
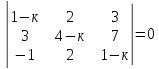 .
2)
.
2)
 .
.
3)
 .
4)
.
4)
 .
.
5)
 .
6)
.
6)
 .
.
7)
 .
8)
.
8)
 .
.
9)
 .
10)
.
10)

11)
 .
12)
.
12)
 .
.
13)
 .
14)
.
14)
 .
.
15)
 .
16)
.
16)
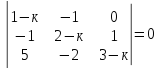 .
.
17)
 .
18)
.
18)
 .
.
19)
 .
20)
.
20)
 .
.
21)
 .
22)
.
22)
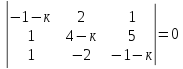 .
.
23)
 .
24)
.
24)
 .
.
25)
 .
.
2.3. Обчисліть визначники четвертого порядку, комбінуючи метод зведення до трикутного вигляду та метод розкладу визначника за елементами деякого рядка (стовпця).
1)
 .
2)
.
2)
 .
3)
.
3)
 .
.
4)
 .
5)
.
5)
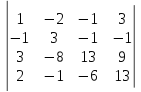 .
6)
.
6)
 .
.
7)
 .
8)
.
8)
 .
9)
.
9)
 .
.
10)
 .
11)
.
11)
 .
12)
.
12)
 .
.
13)
 .
14)
.
14)
 .
15)
.
15)
16) .17)
.17) .18)
.18)
19)
 .
20)
.
20) .
21)
.
21) .
.
22)
 .
23)
.
23)
 .
24)
.
24)
 .
.
25)
 .
.
----------------------------------------------------------------------------------------------------
Самостійна робота №3
Тема 3. Ранг матриці. Основні теоретичні відомості
Нехай задано матрицю А розміру
m n.
Виділимо в матриці А будь-які к
рядків і стільки ж стовпців, де число к
не більше чисел m
і n.
n.
Виділимо в матриці А будь-які к
рядків і стільки ж стовпців, де число к
не більше чисел m
і n.
Визначник порядку к, складений з елементів, що стоять на перетині виділених рядків і стовпців, називають мінором к-го порядку матриці А.
Рангом матриці А називають найвищий порядок відмінного від нуля мінора цієї матриці і позначають r(А).
Ранг
матриці міститься у межах
 r(А)
r(А) .
.
Наприклад,
матриця

має
такі мінори другого порядку:
 ,
,
 ,
,
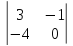 .
.
Мінором третього порядку даної матриці є її визначник.
Мінор, порядок якого визначає ранг матриці, називають базисним. У матриці може бути кілька базисних мінорів.
Ранг матриці можна знаходити так. Якщо в матриці вказано відмінний від нуля мінор к-го порядку, то ранг матриці не менший к. При цьому, якщо всі мінори (к+1)-го порядку дорівнюють нулю, то ранг матриці дорівнює к. Якщо зустрівся ненульовий мінор (к+1)-го порядку, то переходять до дослідження мінорів порядку к+2, тобто процедура продовжується.
На практиці для відшукання рангу високих порядків зручніше використовувати інший метод, який ґрунтується на такому твердженні:
Ранг матриці не зміниться, якщо над нею виконати елементарні перетворення, а саме:
1) переставити місцями два рядки (стовпці);
2) помножити кожен елемент рядка (стовпця) на ненульовий множник;
3) додати до елементів рядка (стовпця) елементи іншого рядка (стовпця), помножені на одне й те саме число.
Скориставшись
елементарними перетвореннями, матрицю
можна звести до вигляду, коли всі її
елементи, крім елементів
 ,
,
 ,
….,
,
….,
 ,
де r
,
де r ,
дорівнюють нулю. Тоді
ранг матриці дорівнює r.
,
дорівнюють нулю. Тоді
ранг матриці дорівнює r.
