Відстань від точки до прямої

Нехай задано пряму L рівнянням і точку 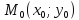(рис.5в). Відстань точки до прямої L дорівнює модулю проекції вектора , де - довільна точка прямої L , на напрям нормального вектора . Отже

Отже, відстань від точки до прямої обчислюється за формулою (14)

Приклади розв’язання типових задач.

1. Нехай точки А(3;1), В(2;-3), С(-1;2) – вершини трикутника АВС. Складіть:

а) загальне рівняння сторони АВ;

б) канонічне рівняння висоти АД;

в) параметричне рівняння медіани ВМ;

г) рівняння прямої, що проходить через точку С(-1;2) паралельно до сторони АВ.

Розв'язання. Побудуємо рис.6 і розглянемо випадки:

а) оскільки відомі координати точок А і В, то, використовуючи формулу (4), складемо рівняння прямої, яка проходить через точки А і В:

, , ,

звідки - загальне рівняння прямої, що містить сторону АВ;

С М

А

Д

В

Рис.6

б) щоб записати канонічне рівняння прямої, потрібно знати точку, через яку проходить пряма, і напрямний вектор. Вектор для висоти АД є нормальним вектором, тоді вектор буде перпендикулярним до вектора (оскільки скалярний добуток ), отже, для прямої АД – напрямним вектором. Записуємо канонічне рівняння прямої АД:

;

в) оскільки точка М – середина відрізка АС, то , . Вектор - напрямний вектор прямої ВМ. За напрямний вектор можна взяти також вектор . Отже, , і параметричні рівняння медіани записуємо так:

, ;

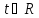г) оскільки пряма, що проходить через точку С(-1;2), паралельна стороні АВ, то за нормальний вектор шуканої прямої беремо вектор - нормальний вектор прямої АВ. Тоді шукане рівняння має вигляд

, або .

2. Обчисліть площу трикутника, обмеженого прямою, що проходить через точки і , і осями координат (рис.7).

Розв'язання. Користуючись формулою (4), складемо рівняння прямої, яка проходить через точки і :

, , , ,

- загальне рівняння прямої .

2

-3 А 6

-4

Знайдемо координати точок перетину прямої з осями координат.

Нехай 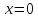, тоді , або . Якщо , то , або .

Отже, пряма перетинає вісь Ох у точці А(3;0), а вісь Оу – у точці В(0;-2). Довжина катетів у трикутнику АОВ відповідно дорівнює: ОА=3, ОВ=2, тоді площа трикутника:

3. Знайдіть відстань між прямими 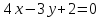та .

Розв'язання. Оскільки задані прямі паралельні, то відстань між ними дорівнює, наприклад, відстані від довільної точки другої прямої до першої. Знаходимо довільну точку на прямій : нехай , тоді . Відстань від точки М(0;) до прямої обчислюємо за формулою (14):

.

4. Визначте, при яких значеннях і прямі та :

а) паралельні; б) збігаються; в) перпендикулярні.

Розв'язання.

а) умова паралельності: , звідси , ;

б) прямі збігаються у разі виконання умови

,

звідси дістаємо дві пари значень , або , ;

в) умова перпендикулярності прямих: , тобто .

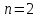Відповідь: а) , ; б) , ; , ; в) , .