
- •Структура модуля.
- •Знання та вміння, якими повинен володіти студент
- •1. Знання на рівні понять, означень, формулювань.
- •2. Уміння в розв’язанні задач.
- •Тема 1. Матриці та дії над ними.
- •Найпростіші дії з матрицями
- •Приклади розв’язання типових задач.
- •Самостійна робота №1
- •Тема 2. Визначник матриці. Властивості визначника.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №2
- •Самостійна робота №3
- •Тема 3. Ранг матриці. Основні теоретичні відомості
- •Приклади розв’язання типових задач.
- •Індивідуальні завдання.
- •Тема 4. Обернена матриця.
- •Матричні рівняння.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №4
- •Тема 5. Розв’язання систем лінійних алгебраїчних рівнянь.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №5
- •Тема 6. Розв’язання систем лінійних алгебраїчних рівнянь матричним методом.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №6
- •Тема 7. Розв’язання систем лінійних алгебраїчних рівнянь методом Гаусса. Основні теоретичні відомості
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №7
- •Структура модуля.
- •Знання та вміння, якими повинен володіти студент
- •1. Знання на рівні понять, означень, формулювань.
- •2. Уміння в розв’язанні задач.
- •Самостійна робота №8
- •Тема 1. Загальні поняття.
- •Тема 2. Координати вектора. Дії над векторами.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Тема 3. Скалярний добуток векторів.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №9
- •Тема 4. Векторний добуток векторів. Основні теоретичні відомості
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №10
- •Структура модуля.
- •Знання та вміння, якими повинен володіти студент
- •1. Знання на рівні понять, означень, формулювань.
- •Самостійна робота №11
- •Тема 1. Пряма лінія.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Тема 2. Загальне рівняння прямої.
- •Канонічне рівняння прямої
- •Рівняння прямої, яка проходить через дві задані точки.
- •Векторне параметричне рівняння прямої
- •Параметричні рівняння прямої
- •Рівняння прямої у відрізках на осях.
- •Рівняння прямої з кутовим коефіцієнтом
- •Відстань від точки до прямої
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №12,13,14,15.
Векторне параметричне рівняння прямої
Нехай
пряма L
проходить через точку
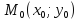 паралельно до напрямного вектора
паралельно до напрямного вектора
 (рис.2). Візьмемо на прямій довільну точку
M(x;y)
і розглянемо радіуси-вектори
(рис.2). Візьмемо на прямій довільну точку
M(x;y)
і розглянемо радіуси-вектори
 та
та
 =
= . Вектори
. Вектори
 i
i
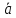 колінеарні, тому
колінеарні, тому
 ,
,
|
|
Рівняння (5) називається векторним параметричним рівнянням прямої. Змінна t, яка може набувати будь-які значення, називається параметром.
|
О L
Рис.2 |
Параметричні рівняння прямої
Позначимо у формулі (3) відношення через t, тобто
|
|
Звідси дістанемо
|
|
Ці рівняння прямої називаються параметричними .
Рівняння прямої у відрізках на осях.
Нехай
пряма L
проходить через дві
точки
 ,
тобто відсікає на осях координат відрізки
довжиною |a| i
|b| (рис.3а).
Підставивши координати цих точок в
рівняння (4) ,дістанемо рівняння (6), яке
називається рівнянням
прямої у відрізках на осях
,
тобто відсікає на осях координат відрізки
довжиною |a| i
|b| (рис.3а).
Підставивши координати цих точок в
рівняння (4) ,дістанемо рівняння (6), яке
називається рівнянням
прямої у відрізках на осях
|
|
Рівняння прямої з кутовим коефіцієнтом
Якщо
пряма L
проходить через точку
 і утворює кут
і утворює кут
 з додатним напрямом осі абсцис (рис.3б),
то число
з додатним напрямом осі абсцис (рис.3б),
то число
 називається кутовим коефіцієнтом
прямої. Обравши довільну точку M(x;y)
на прямій, дістанемо з трикутника
називається кутовим коефіцієнтом
прямої. Обравши довільну точку M(x;y)
на прямій, дістанемо з трикутника


Звідки
|
|
Це
рівняння прямої L
, яка проходить через
точку
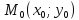 і має кутовий коефіцієнт k
Якщо за точку
і має кутовий коефіцієнт k
Якщо за точку
 візьмемо точку
візьмемо точку
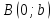 , то дістанемо рівняння (7)
, то дістанемо рівняння (7)
|
|
яке називається рівнянням прямим з кутовим коефіцієнтом.
|
L
O
Рис.3а.б |
Теми 2,3,4,5. Кут між двома прямими. Умови паралельності та перпендикулярності прямих.
Нехай
прямі
 задані рівняннями з кутовими коефіцієнтами
задані рівняннями з кутовими коефіцієнтами
 (рис. 4). Позначимо кути нахилу цих прямих
до осі Ох через
(рис. 4). Позначимо кути нахилу цих прямих
до осі Ох через
 відповідно, причому
відповідно, причому
 .
Тоді гострий кут
.
Тоді гострий кут
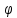 між прямими визначається формулою
між прямими визначається формулою
 . Звідси (8)
. Звідси (8)
|
|
Якщо
прямі
 паралельні , то
паралельні , то
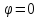 ,
,
 , отже
, отже
 ,
тому умова паралельності прямих (9)
,
тому умова паралельності прямих (9)
|
|
Якщо
прямі
 перпендикулярні, то
перпендикулярні, то
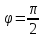 . У цьому разі
. У цьому разі
 не існує. Отже у формулі (8)
не існує. Отже у формулі (8)
 ,
тому умова перпендикулярності прямих
(10)
,
тому умова перпендикулярності прямих
(10)
|
|
Нехай
прямі
 задані загальним рівнянням
задані загальним рівнянням
 i
i
 , тоді : 1) кут
, тоді : 1) кут
 (
( )
між цими прямими визначається
через кут
)
між цими прямими визначається
через кут
 між їхніми нормальними векторами
між їхніми нормальними векторами
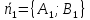
 :
(11)
:
(11)
|
|
Причому
 ,
якщо
,
якщо
 (рис.4а) , і
(рис.4а) , і
 , якщо
, якщо
 (рис.4б)
(рис.4б)
|
Рис.4а,б |
2) умова паралельності прямих (рис.5а) (12)
|
|
3)умова перпендикулярності (рис.5б) (13)
|
|
|
Рис.5а,б |


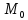













 L
L







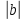

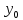































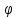




















 d
L
d
L
