
- •Структура модуля.
- •Знання та вміння, якими повинен володіти студент
- •1. Знання на рівні понять, означень, формулювань.
- •2. Уміння в розв’язанні задач.
- •Тема 1. Матриці та дії над ними.
- •Найпростіші дії з матрицями
- •Приклади розв’язання типових задач.
- •Самостійна робота №1
- •Тема 2. Визначник матриці. Властивості визначника.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №2
- •Самостійна робота №3
- •Тема 3. Ранг матриці. Основні теоретичні відомості
- •Приклади розв’язання типових задач.
- •Індивідуальні завдання.
- •Тема 4. Обернена матриця.
- •Матричні рівняння.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №4
- •Тема 5. Розв’язання систем лінійних алгебраїчних рівнянь.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №5
- •Тема 6. Розв’язання систем лінійних алгебраїчних рівнянь матричним методом.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №6
- •Тема 7. Розв’язання систем лінійних алгебраїчних рівнянь методом Гаусса. Основні теоретичні відомості
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №7
- •Структура модуля.
- •Знання та вміння, якими повинен володіти студент
- •1. Знання на рівні понять, означень, формулювань.
- •2. Уміння в розв’язанні задач.
- •Самостійна робота №8
- •Тема 1. Загальні поняття.
- •Тема 2. Координати вектора. Дії над векторами.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Тема 3. Скалярний добуток векторів.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №9
- •Тема 4. Векторний добуток векторів. Основні теоретичні відомості
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №10
- •Структура модуля.
- •Знання та вміння, якими повинен володіти студент
- •1. Знання на рівні понять, означень, формулювань.
- •Самостійна робота №11
- •Тема 1. Пряма лінія.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Тема 2. Загальне рівняння прямої.
- •Канонічне рівняння прямої
- •Рівняння прямої, яка проходить через дві задані точки.
- •Векторне параметричне рівняння прямої
- •Параметричні рівняння прямої
- •Рівняння прямої у відрізках на осях.
- •Рівняння прямої з кутовим коефіцієнтом
- •Відстань від точки до прямої
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №12,13,14,15.
Структура модуля.
Тема 1. Пряма лінія.
Тема 2. Загальне рівняння прямої.
Тема 3. Перетин двох прямих. Кут між ними.
Тема 4. Умова паралельності двох прямих.
Тема 5. Умова перпендикулярності прямих.
Базисні поняття. 1. Декартова прямокутна система координат. 2. Координати точки. 3. Рівняння лінії на площині.
Основні задачі. 1.Побудова рівнянь за різними елементами. 2. Знаходження кута між прямими. 3. Вивчення взаємного розміщення прямих.
Знання та вміння, якими повинен володіти студент
1. Знання на рівні понять, означень, формулювань.
1.1. Загальне рівняння прямої.
1.2. Канонічне рівняння прямої.
1.3. Рівняння прямої, яка проходить через дві точки.
1.4. Векторне параметричне рівняння прямої.
1.5. Параметричні рівняння прямої.
1.6. Рівняння прямої у відрізках на осях.
1.7. Рівняння прямої з кутовим коефіцієнтом.
1.8. Кут між двома прямими.
1.9. Умова паралельності двох прямих.
1.10. Умова перпендикулярності двох прямих.
1.11. Відстань від точки до прямої.
2. Уміння в розв’язанні задач.
2.1. Скласти рівняння прямої, яка проходить через дві точки, через одну точку у заданому напрямі.
2.2. Знаходити відстань між прямими .
2.3. Знаходити точку перетину прямих.
2.4. Знаходити пряму, паралельну даної прямої.
Література: 1. Г.Я. Дутка «Практикум з математики для економістів» – Л. -1998.
2. В. П. Денисюк, В. К. Репета «Вища математика» - К. – 2005.
3. В.А.Подольский, А.М.Суходский «Сборник задач по высшей математике» - М.-1974.
4. И.Л.Зайцев «Элементы высшей математики» - М. – 1972.
5. Н.В.Богомолов «Практические занятия по математике» - М. – 1990.
Самостійна робота №11
Тема 1. Пряма лінія.
ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ.
Рівняння прямих, паралельних осям координат. Рівняння осей координат.
Рівняння прямої, паралельної
осі
 ,
має вигляд
,
має вигляд
 .
.
Всі точки цієї прямої віддалені
від осі
 на одну і ту ж відстань, яка дорівнює
на одну і ту ж відстань, яка дорівнює
 .
.
Рівняння прямої, паралельної
осі
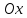 ,
має вигляд
,
має вигляд
 .
.
Всі точки цієї прямої віддалені
від осі
 на одну і ту ж відстань, яка дорівнює
на одну і ту ж відстань, яка дорівнює
 .
.
Якщо
 ,
то пряма розташована справа від осі
,
то пряма розташована справа від осі
 ,
якщо
,
якщо
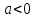 ,
то пряма розташована зліва від осі
,
то пряма розташована зліва від осі
 .
Якщо
.
Якщо
 ,
то пряма співпадає з віссю
,
то пряма співпадає з віссю
 .
У цьому випадку маємо рівняння осі
.
У цьому випадку маємо рівняння осі
 :
:
 .
.
Якщо
 ,
то пряма розташована вище осі
,
то пряма розташована вище осі
 ,
якщо
,
якщо
 ,
то пряма розташована нижче осі
,
то пряма розташована нижче осі
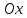 .
Якщо
.
Якщо
 ,
то пряма співпадає з віссю
,
то пряма співпадає з віссю
 .
В цьому випадку маємо рівняння осі
.
В цьому випадку маємо рівняння осі
 :
:
 .
.
Рівняння прямої, яка проходить через початок координат.
Рівняння прямої, яка проходить через початок координат, має вигляд
 ,
,
де
к – кутовий коефіцієнт;
 координати точки.
координати точки.
Кутовий коефіцієнт к дорівнює
тангенсу кута нахилу прямої до осі
 :
:
 .
.
Відмітимо, що кутом нахилу
прямої до осі
 називається кут, на який потрібно
повернути додатний напрям осі
називається кут, на який потрібно
повернути додатний напрям осі
 біля точки перетину прямої з віссю
біля точки перетину прямої з віссю
 ,
проти руху часової стрілки , до співпадіння
з прямою (рис.1).
,
проти руху часової стрілки , до співпадіння
з прямою (рис.1).








Рис.1
Якщо пряма паралельна осі
 ,
то кут нахилу дорівнює
,
то кут нахилу дорівнює
 .
Кут нахилу довільної прямої до осі
.
Кут нахилу довільної прямої до осі
 буде мати значення у межах між
буде мати значення у межах між
 і
і
 (
( ).
).
Якщо
 (гострий кут), то
(гострий кут), то
 ;
якщо
;
якщо
 (тупий кут), то
(тупий кут), то
 .
.
При
 кутового коефіцієнта не існує, так як
кутового коефіцієнта не існує, так як
 не має числового значення. Тобто, довільна
пряма , яка перпендикулярна до осі
не має числового значення. Тобто, довільна
пряма , яка перпендикулярна до осі
 (
( ),
не має кутового коефіцієнта.
),
не має кутового коефіцієнта.
Якщо
на прямій, яка проходить через початок
координат, взяти точку
 ,
то
,
то
 .
.
Кут
 у загальному вигляді пишеться через
аркфункцію:
у загальному вигляді пишеться через
аркфункцію:
 .
.
Бісектриси 1 і 3, 2 і 4 координатних кутів мають відповідно рівняння
 та
та
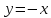 .
.
