Приклади розв’язання типових задач.
1.
Обчисліть
,
якщо
,
,
.
Розв'язання. Оскільки
,
то
.
2.
Знайдіть вектор
,
якщо
,
.
Розв'язання. Послідовно знаходимо
,
.
Тоді
.
3.
Обчисліть площу грані АВС і об’єм
піраміди, вершини якої містяться в
точках
,
,
,
.
Розв'язання.
Знайдемо координати векторів
,
і
,
на яких побудована піраміда:
,
,
.
Площу грані АВС визначаємо
за формулою:
.
Маємо
;
.
Об’єм
піраміди
дорівнює 1/6 частині об’єму паралелепіпеда,
побудованого на векторах
,
і
,
тобто
.
Отже,
4.
Доведіть, що вектори
,
і
утворюють базис, і розкладіть вектор
за цим базисом.
Розв'язання. Нагадаємо, що базисом у просторі називають довільну упорядковану трійку некомпланарних векторів. Тому дані вектори утворюють базис, якщо мішаний добуток цих векторів не дорівнює нулю. Перевіримо цю умову:
.
Отже, вектори
,
і
- базис.
Вектор
розкладений за базисом
,
і
,
якщо
,
невідомі числа (координати вектора
у даному базисі).
Запишемо векторне рівняння у розгорнутому вигляді
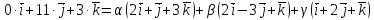
або
Враховуючи умову рівності двох векторів, дістаємо систему рівнянь
Звідси
,
,
.
Отже,
.
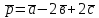Вправи для аудиторної роботи.
1.
Обчисліть
,
якщо
,
,
.
2.
Дано вектори
,
та
.
Знайдіть:
а)
;
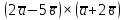б)
.
3.
Обчисліть площу грані АВС і об’єм
піраміди, вершини якої містяться в
точках А(2;4;5) , В(-4;4;-4), С(5;0;3),
(1;2;0).
4.
Доведіть, що вектори
,
,
утворюють базис, і розкладіть вектор
за цим базисом.
5.
Відомо, що точки А(1;2;-1) , В(0;3;1), С(3;2;-4)
та
(а;4;0)
належать одній площині. Знайдіть а.
Самостійна робота №10
10.1. Знайдіть векторний добуток:
1.
,
якщо
,
.
2.
,
якщо
,
.
3.
,
якщо
,
.
4.
,
якщо
,
.
5.
,
якщо
,
.
6.
,
якщо
,
.
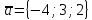7.
,
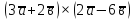якщо
,
8.
,
якщо
,
.
9.
,
якщо
,
.
10.
,
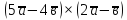якщо
,
.
11.
,
якщо
,
.
12.
,
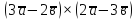якщо
,
.
13.
,
якщо
,
.
14.
,
якщо
,
.
15.
,
якщо
,
.
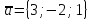16.
,
якщо
,
.
17.
,
якщо
,
.
18.
,
якщо
,
.
19.
,
якщо
,
.
20.
,
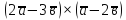якщо
,
.
21.
,
якщо
,
.
22.
,
якщо
,
.
23.
,
якщо
,
.
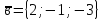24.
,
якщо
,
.
25.
,
якщо
,
10.2. Обчисліть площу грані АВС і об’єм піраміди АВСД, вершини якої містяться в точках:
1.
,
,
,
.
2.
,
,
,
.
3.
,
,
,
.
4.
,
,
,
.
5.
,
,
,
.
6.
,
,
,
.
7.
,
,
,
.
8.
,
,
,
.
9.
,
,
,
.
10.
,
,
,
.
11.
,
,
,
.
12.
,
,
,
.
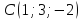13.
,
,
,
.
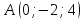14.
,
,
,
.
15.
,
,
,
.
16.
,
,
,
.
17.
,
,
,
.
18.
,
,
,
.
19.
,
,
,
.
20.
,
,
,
.
21.
,
,
,
.
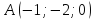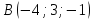22.
,
,
,
.
23.
,
,
,
.
24.
,
,
,
.
25.
,
,
,
.
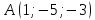10.3.
Доведіть, що вектори
,
і
утворюють базис, і розкладіть
вектор
за цим базисом:
1.
,
,
,
.
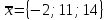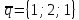2.
,
,
,
.
3.
,
,
,
.
4.
,
,
,
.
5.
,
,
,
.
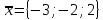6.
,
,
,
.
7.
,
,
,
.
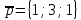8.
,
,
,
.
9.
,
,
,
.
10.
,
,
,
.
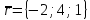11.
,
,
,
.
12.
,
,
,
.
13.
,
,
,
.
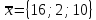14.
,
,
,
.
15.
,
,
,
.
16.
,
,
,
.
17.
,
,
,
.
18.
,
,
,
.
19.
,
,
,
.
20.
,
,
,
.
21.
,
,
,
.
22.
,
,
,
.
23.
,
,
,
.
24.
,
,
,
.
25.
,
,
,
.
--------------------------------------------------------------------------------------------------
Модуль 3. Аналітична геометрія на площині.