
- •Структура модуля.
- •Знання та вміння, якими повинен володіти студент
- •1. Знання на рівні понять, означень, формулювань.
- •2. Уміння в розв’язанні задач.
- •Тема 1. Матриці та дії над ними.
- •Найпростіші дії з матрицями
- •Приклади розв’язання типових задач.
- •Самостійна робота №1
- •Тема 2. Визначник матриці. Властивості визначника.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №2
- •Самостійна робота №3
- •Тема 3. Ранг матриці. Основні теоретичні відомості
- •Приклади розв’язання типових задач.
- •Індивідуальні завдання.
- •Тема 4. Обернена матриця.
- •Матричні рівняння.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №4
- •Тема 5. Розв’язання систем лінійних алгебраїчних рівнянь.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №5
- •Тема 6. Розв’язання систем лінійних алгебраїчних рівнянь матричним методом.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №6
- •Тема 7. Розв’язання систем лінійних алгебраїчних рівнянь методом Гаусса. Основні теоретичні відомості
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №7
- •Структура модуля.
- •Знання та вміння, якими повинен володіти студент
- •1. Знання на рівні понять, означень, формулювань.
- •2. Уміння в розв’язанні задач.
- •Самостійна робота №8
- •Тема 1. Загальні поняття.
- •Тема 2. Координати вектора. Дії над векторами.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Тема 3. Скалярний добуток векторів.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №9
- •Тема 4. Векторний добуток векторів. Основні теоретичні відомості
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №10
- •Структура модуля.
- •Знання та вміння, якими повинен володіти студент
- •1. Знання на рівні понять, означень, формулювань.
- •Самостійна робота №11
- •Тема 1. Пряма лінія.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Тема 2. Загальне рівняння прямої.
- •Канонічне рівняння прямої
- •Рівняння прямої, яка проходить через дві задані точки.
- •Векторне параметричне рівняння прямої
- •Параметричні рівняння прямої
- •Рівняння прямої у відрізках на осях.
- •Рівняння прямої з кутовим коефіцієнтом
- •Відстань від точки до прямої
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота №12,13,14,15.
Тема 4. Векторний добуток векторів. Основні теоретичні відомості
Векторним добутком вектора
 на вектор
на вектор
 називають вектор
називають вектор
 ,
який задовольняє такі три умови:
,
який задовольняє такі три умови:
1)
модуль вектора
 обчислюють за формулою:
обчислюють за формулою:
 ,
,
де
 - кут між векторами
- кут між векторами
 і
і
 ;
;
2)
вектор
 перпендикулярний до кожного з векторів
перпендикулярний до кожного з векторів
 і
і
 ;
;
3)
вектори
 ,
,
 і
і
 утворюють праву трійку,
тобто якщо дивитися з кінця результуючого
вектора
утворюють праву трійку,
тобто якщо дивитися з кінця результуючого
вектора
 ,
то найкоротший поворот від першого
вектора
,
то найкоротший поворот від першого
вектора
 до другого вектора
до другого вектора
 видно проти годинникової стрілки
(рис.1).
видно проти годинникової стрілки
(рис.1).


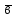



Рис.1


Позначення векторного добутку:
 ,
,
 .
.
З
означення векторного добутку безпосередньо
випливають векторні рівності між ортами
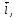

 :
:

Властивості векторного добутку.
Розглянемо алгебраїчні та геометричні властивості векторного добутку:
1)
геометричний зміст векторного добутку:
модуль векторного добутку дорівнює
площі паралелограма, побудованого на
прикладених до спільного початку
векторах
 і
і
 (рис.2).
(рис.2).


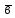




 S
Рис.2
S
Рис.2
2) антикомутативність множення:

3)
 ;
;
 ;
;
4)
 ;
;
5)
два ненульові вектори
 колінеарні тоді і тільки тоді, коли
векторний добуток цих векторів дорівнює
нуль-вектору, тобто
колінеарні тоді і тільки тоді, коли
векторний добуток цих векторів дорівнює
нуль-вектору, тобто

Зокрема,

Зауваження. Якщо відомі координати вершин трикутника АВС, то його площу доцільно шукати за формулою

Векторний добуток векторів, заданих координатами.
Нехай
вектори
 ,
,
 задані своїми координатами у ПДСК. Тоді
векторний добуток знаходять за формулою
задані своїми координатами у ПДСК. Тоді
векторний добуток знаходять за формулою

або

Мішаний добуток векторів.
Мішаним
(векторно-скалярним) добутком
трьох векторів
 ,
,
 і
і
 називають число
називають число
 ,
рівне скалярному добутку вектора
,
рівне скалярному добутку вектора
 на вектор
на вектор
 :
:

Розглянемо властивості мішаного добутку.
1. Якщо в мішаному добутку поміняти місцями які-небудь два множники, то мішаний добуток змінить знак, наприклад:
 .
.
2. При циклічному переставленні множників мішаний добуток не змінюється.
3. У мішаному добутку знаки векторного і скалярного добутків можна міняти місцями:
 .
.
4.
Геометричний зміст мішаного добутку:
модуль мішаного добутку
 чисельно дорівнює об’єму паралелепіпеда,
побудованого на прикладених до спільного
початку векторах
чисельно дорівнює об’єму паралелепіпеда,
побудованого на прикладених до спільного
початку векторах
 ,
,
 і
і
 (рис.3), тобто
(рис.3), тобто












Рис.3
 S
S


Зауваження.
Об’єм піраміди,
побудованої на векторах
 ,
,
 і
і
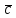 ,
дорівнює 1/6 частини об’єму паралелепіпеда,
тобто
,
дорівнює 1/6 частини об’єму паралелепіпеда,
тобто

5.
Якщо
 ,
то вектори
,
то вектори
 ,
,
 і
і
 утворюють праву трійку,
а якщо
утворюють праву трійку,
а якщо
 ,
то ліву трійку.
,
то ліву трійку.
6. Умова компланарності трьох векторів.

Мішаний добуток трьох векторів, заданих координатами.
Нехай вектори
 ,
,
 ,
,
 задані своїми координатами в ПДСК.
Знайдемо мішаний добуток цих векторів,
використовуючи формули скалярного і
векторного добутку векторів, заданих
координатами. Маємо
задані своїми координатами в ПДСК.
Знайдемо мішаний добуток цих векторів,
використовуючи формули скалярного і
векторного добутку векторів, заданих
координатами. Маємо


 .
.
Дістали розклад визначника третього порядку за елементами першого рядка. Отже,

Зауваження.
Компланарність ненульових векторів
 ,
,
 і
і
 встановлюють так: якщо визначник
встановлюють так: якщо визначник
 ,
,
то
вектори
 ,
,
 і
і
 – компланарні, якщо визначник відмінний
від нуля, то вектори не компланарні.
– компланарні, якщо визначник відмінний
від нуля, то вектори не компланарні.
