курсовая работа / МСУ к.р 51в / Слайды1
.docИСХОДНЫЕ ДАННЫЕ
Таблица 1 - Параметры гидросистемы
|
Наименование параметра |
Обозн. |
Номер магистрали |
||||
|
1 |
2 |
3 |
4 |
5 |
||
|
Диаметр, м |
dтр |
0,014 |
0,015 |
0,01 |
0,02 |
0,015 |
|
Длина, м |
l |
1,5 |
1 |
2 |
0,55 |
0,5 |
|
Толщина стенки трубопровода, м |
|
3*10-4 |
3*10-4 |
3*10-4 |
3*10-4 |
3*10-4 |
|
Коэф-нт местных сопротивлений |
|
5 |
3 |
505 |
2 |
1.5 |
|
Давление потребителя, Па |
p |
0.1*106 |
0.15*106 |
0.19*106 |
--- |
--- |
|
Рабочая жидкость |
Масло веретенное
АУ:
|
|||||
|
Материал трубопровода |
Сталь: Етр=2,1*1011 Па |
|||||
|
Коэффициент потерь на трение при турбулентном потоке |
|
|||||
|
Номер схемы |
10 |
|||||
;
Ес=1,7*108
Па. 
ГРАФИЧЕСКИЕ ФОРМЫ МОДЕЛИ
Рисунок 2 – Схема динамической модели гидросистемы Рисунок 3 – Орграф гидросистемы
УЗЛОВОЙ МЕТОД ФОРМИРОВАНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
Таблица 2 – Матрица инцидентности.
|
Узел |
Ветви |
|||||||||||||||
|
инерционные |
диссипативные |
упр. |
Источники потенциалов |
|||||||||||||
|
m1 |
m2 |
m3 |
m4 |
m5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
-1 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
0 |
+1 |
-1 |
0 |
0 |
0 |
0 |
|
2 |
0 |
-1 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
+1 |
0 |
-1 |
0 |
0 |
0 |
|
3 |
0 |
0 |
-1 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
+1 |
0 |
0 |
-1 |
0 |
0 |
|
1* |
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
0 |
-1 |
0 |
-1 |
0 |
0 |
0 |
1 |
0 |
|
2* |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
0 |
-1 |
-1 |
0 |
0 |
0 |
0 |
1 |
|
подматрица |
Аи |
Ад |
Ау |
Ав |
||||||||||||
На основании матрицы инцидентности, выполним следующие подматрицы:
,
,
.
В диагональной матрицы параметров элементов гидросистемы:
,
,
.
ФОРМУЛЫ УЗЛОВОГО МЕТОДА
Матрица потенциалов источников Рв, упругих Ру и диссипативных Рд, компонентов:
,
,
.
Матрица фазовых переменных типа потока – это столбец:
Вычислим матричное произведение слагаемых правой части уравнения (1):
,
,
.
ПАРАМЕТРЫ ЭЛЕМЕНТОВ ГИДРОСИТЕМЫ
Таблица 3 – Расчет параметров гидросистемы.
|
Параметры |
Формула |
МАГИСТРАЛЬ |
||||
|
1 |
2 |
3 |
4 |
5 |
||
|
1) Площадь сечения магистрали |
|
1.539*10-4 |
1.766*10-4 |
7.85*10-5 |
3.14*10-4 |
1.766*10-4 |
|
2) Объем участка трубопровода |
|
2.309*10-4 |
1.766*10-4 |
1.57*10-4 |
1.727*10-4 |
8.83*10-5 |
|
3) Доля объема |
|
0.28 |
0.214 |
0.19 |
0.209 |
0.107 |
|
4) Коэффициент массы |
|
8.382*106 |
4.87*106 |
2.191*107 |
1.506*106 |
2.435*106 |
|
5) Коэффициент линейных гидравлических потерь |
|
2.059*107 |
1.042*107 |
1.055*108 |
1.813*106 |
5.212*106 |
|
6) Коэффициент нелинейных потерь |
|
5.446*1010 |
2.574*1010 |
3.908*1011 |
3.358*109 |
1.287*1010 |
|
7) Коэффициент жесткости участка |
|
2.534*1012 |
4.323*1012 |
5.549*1012 |
4.469*1012 |
1.727*1013 |
МОДЕЛИРОВАНИЕ И АНАЛИЗ СТАТИЧЕСКОЙ МОДЕЛИ
Статическая
модель:
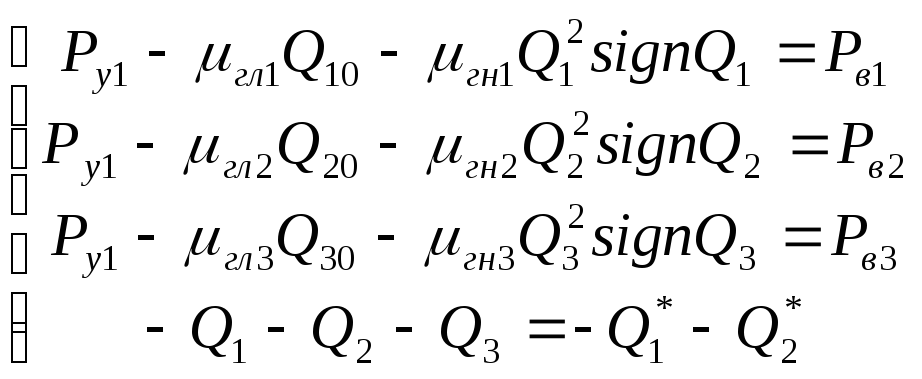
Матрица Якоби:
Таблица 4 – Результаты статического анализа
|
Фазовые координаты |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ИНТЕГРИРОВАНИЕ ДИНАМИЧЕСКОЙ МОДЕЛИ
С учетом ранее произведенных расчетов, запишем систему дифференциальных уравнений, характеризующую динамическую модель гидроситемы:
Так как система дифференциальных уравнений нелинейная, то элементами матрицы Якоби, являются частные производные по фазовым координатам:
ИНТЕГРИРОВАНИЕ ДИНАМИЧЕСКОЙ МОДЕЛИ
Определим
и при
,
значения фазовых координат, определены
при анализе статического состояния:
Начальное значение:
Конечное значение:
Произведем расчет значений матрицы Якоби с учетом начальных значений расходов:
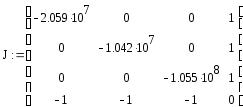
АНАЛИЗ ПЕРЕХОДНЫХ ПРОЦЕССОВ
Рисунок 4 – Показатели качества устойчивости системы Рисунок 5 – Переходный процесс системы
По графикам 4 и 5, видно, что при внешних воздействиях на гидросистему, происходит переходный процесс, при котором система переходит из одного установившегося состояния в другое. Это говорит о том, что данная система устойчива.