7.3. Рефрактометрические методы анализа

Исследование преломления света при прохождении луча через границу раздела прозрачных однородных сред (рефрактометрия) является, по-видимому, старейшим из опти­ческих методов, известным еще по работам И. Ньютона, Л. Эйле­ра, М. В. Ломоносова и др.

В 80-е годы XIX в. рефрактометры начали использовать в практике работы заводских лабораторий и значение рефракто­метрических методов стало быстро возрастать. Рефрактометрический метод сохранил свое значение и в настоящее время как метод анализа сложных смесей, исследования свойств веществ и взаимодействия в химических системах.

Показатель преломления и полное внутреннее отражение

При падении луча света на границу (раздела двух прозрачных сред происхо­дит частичное отражение света от поверх­ности раздела и частичное распростране­ние света в другой среде (рис. 7.7). На­правление луча во второй среде изменяется в соответствии с законом преломления:

Величину n_2(отн) называют относительным показа­телем (коэффициентом) преломления второй среды по отноше­нию к первой. Показатель преломления по отношению к вакууму называют абсолютным показателем преломления:

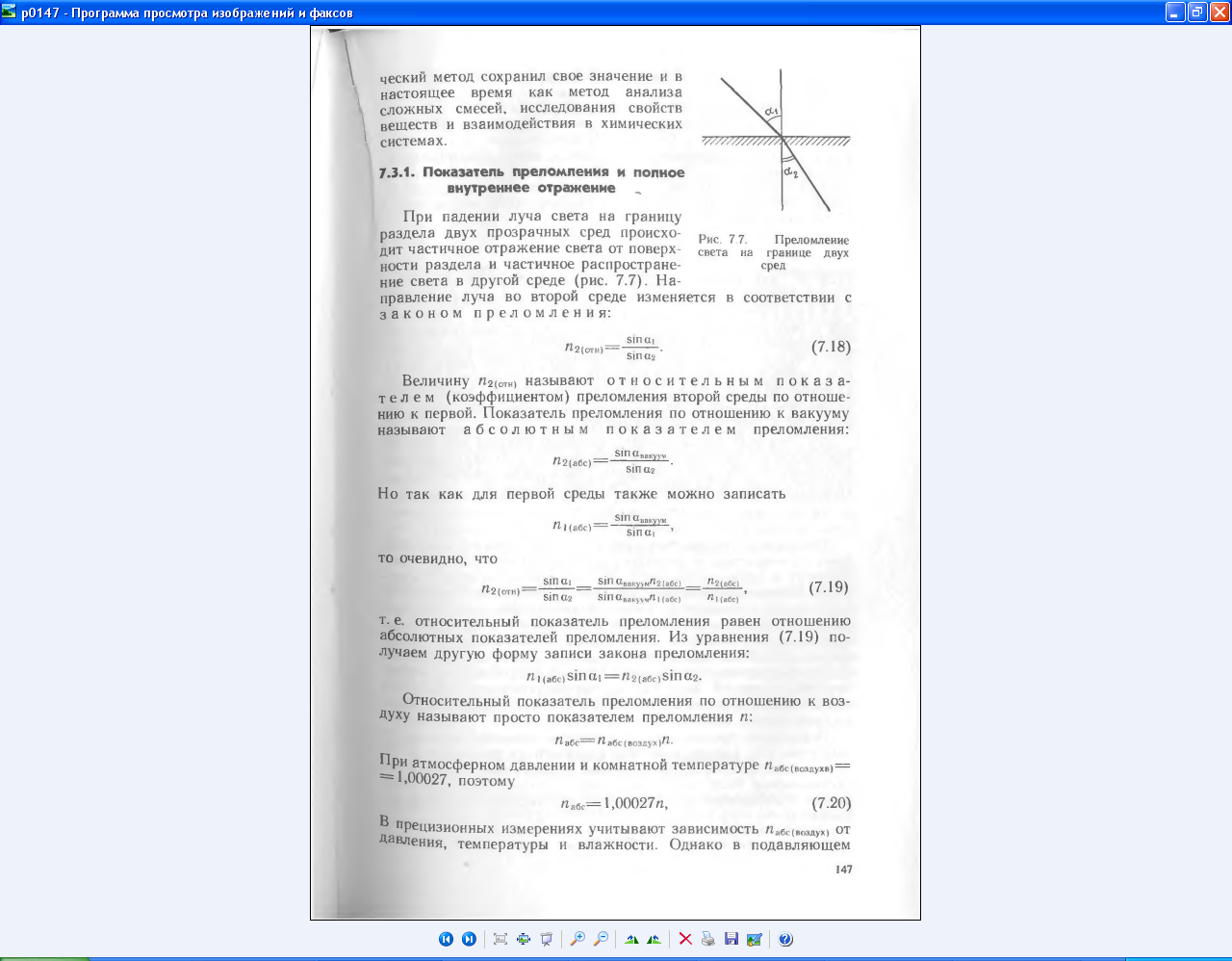
Но так как для первой среды также можно записать

то очевидно, что

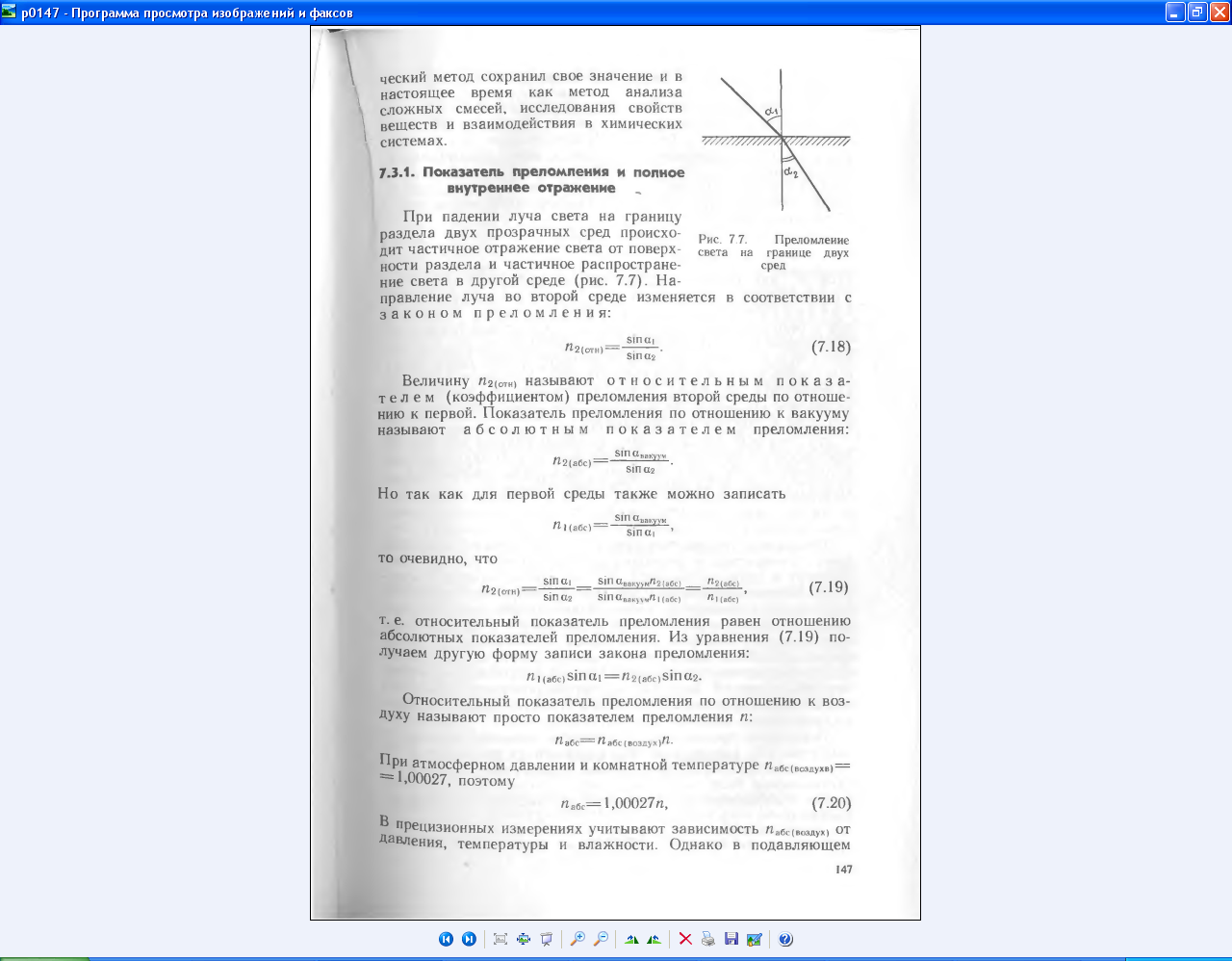
т. е. относительный показатель преломления равен отношению абсолютных показателей преломления. Из уравнения (7.19) по­лучаем другую форму записи закона преломления:

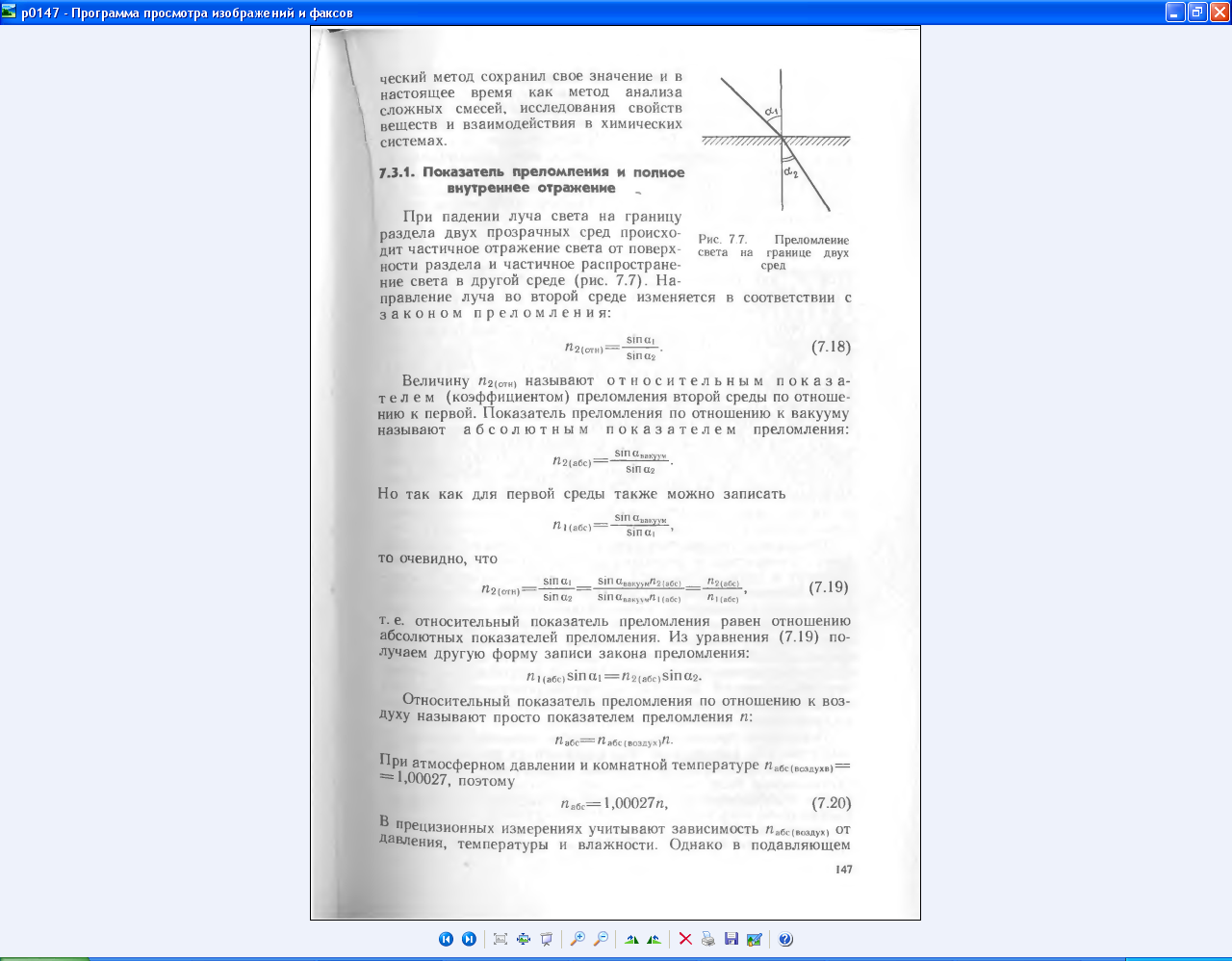
Относительный показатель преломления по отношению к воздуху называют просто показателем преломления п:

При атмосферном давлении и комнатной температуре П_{абс(воздуха)} = 1,00027, поэтому,

В прецизионных измерениях учитывают зависимость п_{абс(возДух)} от давления, температуры и влажности. Однако в подавляющем большинстве случаев формула (7.20) оказывается вполне при­годной.

Опыт показывает, что если свет переходит, например, из воз­духа в какую-то конденсированную, более преломляющую среду, то угол падения всегда больше угла преломления. При переходе из среды, более преломляющей, в среду, менее преломляющую, угол преломления α₁ оказывается больше угла падения α₂ . Если угол преломления α₂ =90° (см. рис. 7.8), то, очевидно, прелом­ления вообще не произойдет, и поскольку sin90°=l, формула (7.18) переходит в

Угол α₁, при котором преломление не происходит, называют углом полного внутреннего отражения, а также предельным или критическим углом. Например, при переходе светового луча из стекла в воздух под углом в 40° угол преломления составляет 90° и, следовательно, при угле па­дения α₁>40° преломления не происходит, а свет будет полно­стью отражаться от поверхности раздела. Уравнение (7.21) по­казывает, что по условию полного внутреннего отражения можно рассчитать показатель преломления. Это соотношение часто ис­пользуют в практике рефрактометрии.

На показатель преломления оказывают влияние, как физико-химические свойства вещества, так и многие внешние условия. Волновая теория света связывает показатель преломления со скоростью света в вакууме C и в данной среде V₂:

n₂ = c/V₂.

Показатель преломления зависит от длины волны падающего света, температуры и некоторых других внешних условий. Тем­пературу и длину волны света, при которой производится изме­рение, обычно указывают у символа п. Например, запись n²⁵₅₈₉означает, что показатель преломления измерен при 25°С для желтой D-линии натрия с длиной волны 589 нм. В качестве ниж­него индекса у п вместо длины волны часто указывают только буквенный символ линии (D для желтой линии натрия 589 нм, С для красной линии водорода 656 нм и т. д.) и вместо, напри­мер, n²⁵₅₈₉ пишут n²⁵_D. Величину π_∞ характеризующую показатель преломления при бесконечно большой длине волны, находят экстраполяцией зависимости n=f(λ).

Показатель преломления и плотность вещества изменяются симбатно, т. е. с ростом плотности происходит увеличение пока­зателя преломления. Теоретическими и экспериментальными ис­следованиями было установлено, что некоторая функция пока­зателя преломления f(n) прямо пропорциональна плотности ве­щества ρ:

f(n)=rρ.

Коэффициент пропорциональности г назвали удельной реф­ракцией. При умножении г на молярную массу М получают молярную рефракцию R:

R=Mr.

Для выражения функции f(n) и, следовательно, для расчета рефракции было предложено несколько уравнений. Наибольшее распространение получила теоретически обоснованная формула • Лоренц —Лоренца:

Величина рефракции, найденная по этой формуле, практически не зависит от внешних условий (температуры, давления и т.д.). В органической химии широко применяется правило адди­тивности молярных рефракций, в соответствии с которым молярная рефракция соединения равна сумме атомных рефракций элементов, образующих это соединение, а рефракция смеси равна сумме молярных рефракций ее составных частей. Молярную рефракцию растворов можно поэтому рассматривать как линейную функцию их состава, выраженного в молярных долях. Рассчитывались также рефракции связей и некоторые другие рефрактометрические константы, пользуясь которыми можно определять рефракции сложных соединений без проведе­ния экспериментальных измерений. Эти величины представляют интерес и в настоящее время для идентификации органических соединений, определения их структуры и проведения различных физико-химических расчетов. Можно отметить также, что моляр­ная рефракция по Лореиц—Лорентцу R_л-л является мерой поляризуемости молекул а:

R_л__л=2,52.10²⁴ α. (7.22)

Поляризуемость, как известно, является характеристикой дефор­мируемости молекул под действием электрического поля.

Зависимость показателя преломления от длины волны падаю­щего света называют дифракционной дисперсией или просто дисперсией. Обычно мерой дисперсии считают разность показателей преломления при двух длинах волн. Отно­сительное изменение дисперсии, например, в ряду гомологиче­ских соединений обычно превышает изменение показателя пре­ломления.