3. Сколько существует для заданной прямой

а) параметрических уравнений;

б) канонических уравнений?

4. Запишите векторно-параметрические уравнения прямой.

5. Пусть прямая задана в виде пересечения двух плоскостей: и . Выпишите какой–либо направляющий вектор этой прямой.

6. Пусть прямая задана в виде пересечения двух плоскостей. Как перейти для этой прямой к

а) параметрическим уравнениям;

б) каноническим уравнениям?

7. Найдите угол между прямыми и

(Рассмотрите различные сочетания способов задания двух прямых).

8. Найдите угол между прямой и плоскостью (рассмотрите различные сочетания способов задания прямой и плоскости).

9. Вычислите расстояние от точки М₀(x₀;y₀;z₀) до прямой

а) x=x₀+lt, y=y₀+mt, z=z₀+nt;

б) ;

в)

10. Запишите условия, при которых две заданные прямые

а) совпадают;

б) параллельны различны;

в) пересекаются;

г) скрещиваются

(Рассмотрите различные сочетания способов задания прямых ).

11. Пусть прямые x=x₁+l₁t, y=y₁+m₁t, z=z₁+n₁t и x=x₂+l₂t, y=y₂+m₂t, z=z₁+n₁t скрещиваются.

а) Как вычислить расстояние между этими прямыми?

б) Опишите алгоритм нахождения общего перпендикуляра к этим прямым.

12. Пусть заданы прямая x=x₀+lt, y=y₀+mt, z=z₀+nt и плоскость Запишите условия, при которых

а) прямая лежит в плоскости;

б) прямая параллельна плоскости;

в) прямая пересекает плоскость;

г) прямая перпендикулярна плоскости.

(Рассмотрите такую задачу для других способов задания прямой и плоскости).

Примеры: 1. Запишите параметрические уравнения прямой, заданной в виде пересечения плоскостей

Р е ш е н и е: Вектор перепендикулярен плоскости (1), вектор перпендикулярен плоскости (2). Следовательно, вектор будет направляющим для данной прямой.Можно взять в качестве направляющего и вектор . Выбираем какое-либо частное решение исходной системы, например, (2;0;1), получаем точку на данной прямой. Таким образом, по точке М₀ (2;0;1) и направляющему вектору записываем (рис.5)

О т в е т :

2.Запишите уравнение прямой, которая проходит через точку М₀(1;4;2) перпендикулярно плоскости 2х–5у–z–7=0.

Р е ш е н и е: Вектор 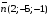перпендикулярен заданной плоскости и, следовательно, параллелен искомой прямой. Поэтому, например, каноническими уравнениями этой прямой будут уравнения

.

О т в е т: (рис.6).

3. Докажите, что прямые и скрещиваются.

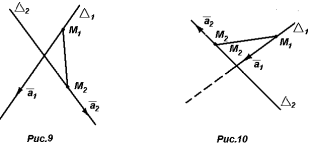
Р е ш е н и е:Случай скрещивания двух прямых можно установить, проанализировав взаимное расположение направляющих векторов и вектора-мостика . Только в случае скрещивания прямых эти три вектора некомпланарны. Итак, выпишем направляющие векторы этих прямых , . Найдем какой-либо вектор-мостик прямых: , , 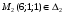отсюда . Векторы , 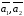некомпланарны, как известно, тогда и только тогда, когда их смешанное произведение не равно нулю. В данном случае, . Таким образом, утверждение доказано (рис.7,8,9,10).

4. Запишите уравнения прямой, проходящей через точку и параллельной прямой

Р е ш е н и е: Любая прямая, параллельная данной, может быть за-

дана системой

Подберем таким образом, чтобы точка М₀ удовлетворяла

системе (*): , Получим

О т в е т: (рис.11).

5. Найдите угол между прямой и плоскостью

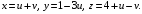
Р е ш е н и е: Направляющий вектор прямой– , нормальный вектор плоскости– . Поэтому

Тогда (а как записывался бы ответ в случае, если бы получили, что ?)

О т в е т: .(рис.12).

7. Вычислите расстояние от точки М₀(1;2;–3) до прямой .

Р е ш е н и е:

1) Способ первый.

Через точку М₀ проведем плоскость,

перпендикулярную данной прямой: .

Затем найдем точку пересечения этой плоскости с заданной прямой. Для этого решим систему

Отсюда . Поэтому решением рассматриваемой системы будет точка . Расстояние между точками M₀, N₀ и будет искомым: (лин. ед.).(см.рис.13).

2)Способ второй

Эту задачу можно решить векторным способом. Возьмем какие-либо точку и направляющий вектор на заданной прямой, например, М₁(4;1;2), Затем построим параллелограмм на векторах. Очевидно, длина высоты h этого параллелограмма и будет искомым расстоянием (рис.14):

где , а (см. тему «Векторное умножение векторов»).

, поэтому .

Но тогда (лин. ед.).

О т в е т: (лин. ед.).

“ПРЯМАЯ по теме В ПРОСТРАНСТВЕ”

1. Дана прямая х=1-3t, y=2t, z=5+t.

1) Укажите какой-либо направляющий вектор этой прямой.

2).Лежит ли точка на этой прямой?

3) Запишите какие-либо канонические уравнения заданной прямой.

4) Запишите какие-либо параметрические уравнения прямой, проходящей через точку А(3;1;5) параллельно заданной

прямой.

5) Лежит ли данная прямая в плоскости x+y+z-6=0?

6) Будет ли прямая x=2t, y=1+t, z=5-t скрещиваться с данной прямой?

7) Вычислите косинус угла между заданной прямой и прямой x=5-t, y=4+3t, z=6+2t.

8) Вычислите расстояние от точки С(1;0;0) до заданной прямой.

9) Напишите какое-либо общее уравнение плоскости, проходящей через точку

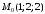
перпендикулярно заданной прямой.

2. Дана прямая

1) Укажите какой-либо направляющий вектор этой прямой.

2) Лежит ли точка на этой прямой?

3) Запишите какие-либо канонические уравнения этой прямой.

4) Вычислите косинус угла между плоскостью 2x+y+3z+7=0 и заданной прямой.

3. Для прямой

1) укажите какой-либо направляющий вектор;

2) запишите какие-либо ее параметрические уравнения;

3) выясните, будет ли она совпадать с прямой

4. Запишите какие-либо канонические уравнения прямой, проходящей через точки и .

5. Запишите какие-либо канонические уравнения прямой, проходящей через точку А(2;1;3) параллельно оси Ох.

6. Запишите какие-либо параметрические уравнения прямой, проходящей через точку А(3;0;-2)

перпендикулярно плоскости 4x-2y+z-25=0.

7. Запишите прямую в виде пересечения двух плоскостей,.одна из которых параллельна оси Ox, другая-оси Oy.