Вариант 11

1. Напишите общее уравнение плоскости, проходящей через точки , , .

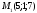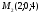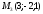2. Вычислите координаты точки, симметричной точке 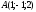относительно прямой .

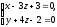3. Найдите параметрические уравнения прямой, являющейся проекцией прямой 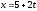, , 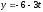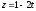на плоскость , , .

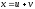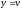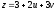4. Известны координаты вершин треугольника ABC: , , 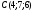. Запишите уравнения высоты этого треугольника, проведенной из вершины B.

5. При каких значениях параметров A и m прямая 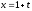, , 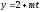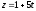лежит в плоскости ?

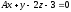6. Даны две параллельные плоскост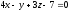и: и 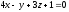. Выясните, лежит ли точка между этими плоскостями?

Вариант 12

1. Напишите общее уравнение плоскости, содержащей точку 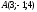и прямую .

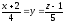2. Вычислите координаты точки, симметричной точке 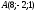относительно плоскости , , .

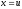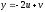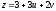3. Найдите параметрические уравнения прямой, являющейся проекцией прямой 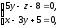на плоскость .

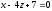4. Напишите уравнения перпендикуляра, проведенного через точку 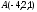к прямой , , .

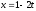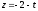5. При каком значении параметра n прямые 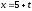, , 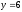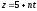и , , 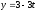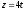пересекаются?

6. Две грани куба лежат на плоскостях 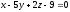, 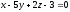. Выясните, может ли точка располагаться внутри такого куба?

Вариант 13

1. Напишите общее уравнение плоскости, содержащей прямые и , , .

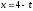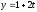2. Вычислите координаты точки, симметричной точке 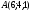относительно прямой .

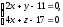3. Найдите параметрические уравнения прямой, являющейся проекцией прямой 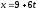, , 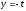на плоскость , , .

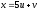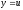4. Известны координаты вершин треугольника ABC: 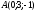, , 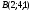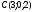. Запишите уравнения высоты этого треугольника, проведенной из вершины B.

5. При каких значениях параметров С и m прямая 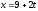, , 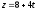перпендикулярна плоскости ?

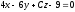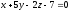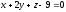6. Даны две пересекающиеся плоскости: и . Выясните, лежат ли точк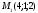и и 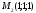в смежных двугранных углах, образованных этими плоскостями?

Вариант 14

1. Напишите общее уравнение плоскости, содержащей прямые 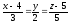и , , .

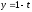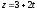2. Вычислите координаты точки, симметричной точке 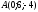относительно плоскости , , .

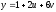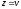3. Найдите параметрические уравнения прямой, являющейся проекцией прямой на плоскость .

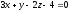4. Напишите уравнения перпендикуляра, проведенного через точку 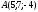к прямой , , .

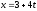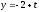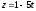5. При каком значении параметра В плоскости и перпендикулярны?

6. Даны две параллельные плоскост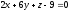и: и 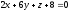. Выясните, лежит ли точка 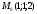между этими плоскостями?

Вариант 15

1. Напишите общее уравнение плоскости, проходящей через прямую 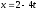, , параллельно прямой .

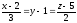2. Вычислите координаты точки, симметричной точке 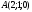относительно прямой .

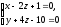3. Найдите параметрические уравнения прямой, являющейся проекцией прямой 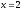, , 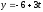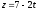на плоскость , , .

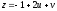4. Известны координаты вершин треугольника ABC: , , 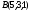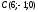. Запишите уравнения высоты этого треугольника, проведенной из вершины B.

5. При каких значениях параметров С и А прямая , , 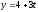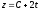не пересекает плоскость ?

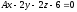6. Две грани куба лежат на плоскостях 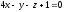, . Выясните, может ли точка 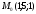располагаться внутри такого куба?