
- •III.1. Регулярная поверхность.
- •III.2. Линии на поверхности.
- •III.3. Касательная плоскость и нормаль поверхности.
- •III.4. Первая основная квадратичная форма поверхности.
- •III.5. Метрика на поверхности.
- •III.6. Кривизна линий на поверхности.
- •III.7. Индикатриса кривизны.
- •III.8. Классфикация обыкно венных точек поверхности.
- •III.9. Главные кривизны на поверхности.
- •III.10. Вычисление полной и средней кривизн поверхности.
- •III.11. Плоскость, сфера, псевдосфера.
III.10. Вычисление полной и средней кривизн поверхности.
Рассматриваем
регулярную поверхность
 в окрестности точки
в окрестности точки
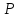 .
Дифференциалы
.
Дифференциалы
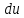 ,
,
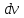 из (III.7.1) подставим в выражение (III.6.4) для
нормальной кривизны поверхности. После
сокращение на
из (III.7.1) подставим в выражение (III.6.4) для
нормальной кривизны поверхности. После
сокращение на
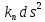 приходим к равенству
приходим к равенству
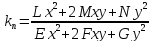 .
.
Отсюда получаем
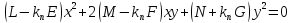 .
.
Дифференцируем
это равенство по
 и по
и по
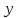 :
:

Главные
направления в касательной плоскости
определяются этой системой уравнений,
если она имеет ненулевые решения, т.е.
в случае
 .
.
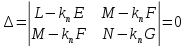 .
.
Значение определителя
 .
.
Главные
кривизны
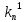 ,
,
 есть корни выписанного уравнения.
Воспользуемся теоремой Виетта:
есть корни выписанного уравнения.
Воспользуемся теоремой Виетта:
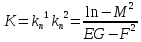 ,
,
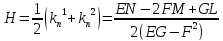 .
.
Полная и средняя кривизны поверхности найдены без вычисления главных кривизн.
III.11. Плоскость, сфера, псевдосфера.
Проведем вычисления кривизн для указанных поверхностей.
-
плоскость. Ее задание
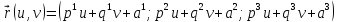 .
.
Находим частные производные:
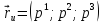 ,
,
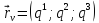 ,
,
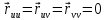 .
.
По
вычислительным формулам для
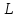 ,
,
 ,
,
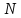 ,
п. III.6, имеем:
,
п. III.6, имеем:
 .
Значит, см. формулы для
.
Значит, см. формулы для
 и
и
 в п. III.10,
в п. III.10,
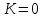 ,
,
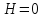 .
.
Полная и средняя кривизны плоскости равны нулю;
-
сфера. Поверхность задается функцией
г (u, v) = (a cos u cos v, a cos u sin v, a sin u). Находим частные производные:
 .
.
Находим частные производные:
 ,
,
 ,
,
 ,
,
 ,
,
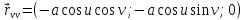 .
.
Вычисляем коэффициенты первой квадратичной формы сферы, см. (III.4.2):
 ,
,
 ,
,
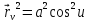 .
.
Детерминант первой квадратичной формы:
 .
.
Вычисляем коэффициенты второй квадратичной формы, п. III.6:
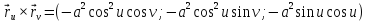 ,
,
 ,
,
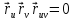 ,
,
 .
.
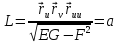 ;
;
 ;
;
 .
.
Наконец, вычисляем полную и среднюю кривизну, п. III.10:
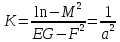 ,
,
 .
.
Полная и средняя кривизны сферы постоянны и положительны;
-
псевдосфера. Это поверхность, полученная в результате вращения трактрисы

вокруг оси Oz. Поверхность задается функцией
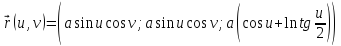 .
.
Находим частные производные
 ,
,
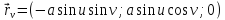 ,
,
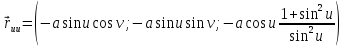 ,
,
 ,
,
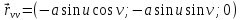 .
.
Коэффициенты первой квадратичной формы псевдосферы
 ,
,
 ,
,
 ,
,
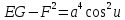 .
.
Находим произведения векторов и коэффициенты второй квадратичной формы поверхности:
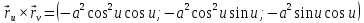 ,
,
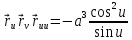 ,
,
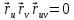 ,
,
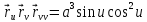 .
.
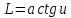 ;
;
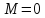 ;
;
 .
.
Вычисляем полную и среднюю кривизну, п. III.10:
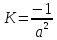 ,
,
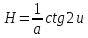 .
.
Полная кривизна псевдосферы отрицательна и постоянна. За это свойство рассматриваемая поверхность названа псевдосферой.
Каждая
точка плоскости есть точка уплощения,
п. III.8. Существуют и другие поверхности,
имеющие нулевую полную кривизну.
Например, цилиндр
 - поверхность нулевой полной кривизны.
- поверхность нулевой полной кривизны.
