4. Выделение единичных контуров

Определение по карте Карно конечных конъюнкций выполняется по следующим правилам:

Все соседние единичные клетки должны быть заключены в прямоугольные единичные контуры.
Число единиц в контуре должно выражаться числами 2⁰=1, 2¹=2, 2²=4, 2³=8 и т.д.
Единичные контуры не должны содержать внутри себя нулей.
Построение единичного контура следует начинать с единиц, которые могут войти только в один единственный контур.
Одна и та же единица может входить в несколько единичных контуров.
Единичные контуры могут накладываться друг на друга.
Единичные контуры могут содержать разрыв на границе карты.
Каждой единичной клетке соответствует исходная конъюнкция (конституент единицы) соответствующего набора.
Увеличение размеров единичного контура приводит к уменьшению длины конечной конъюнкции.
В единичном контуре, объединяющем две клетки, один из аргументов, меняющий свое значение, не входит в конечную конъюнкцию.
В единичном контуре, объединяющем более двух клеток, в конечную конъюнкцию не входят аргументы, чьи границы пересекаются площадью, ограниченной данным контуром.
Единичные клетки должны объединяться в наибольшие контуры.
Количество контуров должно быть минимальным.

В соответствии с изложенными правилами получаем три единичных контура (рисунок 3).

Рисунок 3 - Карта Карно с выделенными единичными контурами.

5. Составление минимальной дизъюнктивной нормальной формы мднф

Для выделенных контуров записываем конечные конъюнкции , где i – номер контура:

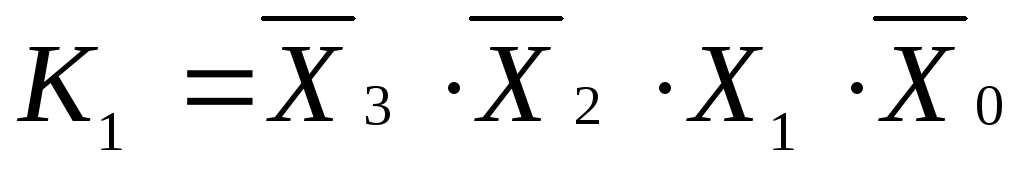
	(2)
	(3)
	(4)

Из конечных конъюнкций составляем выражение:

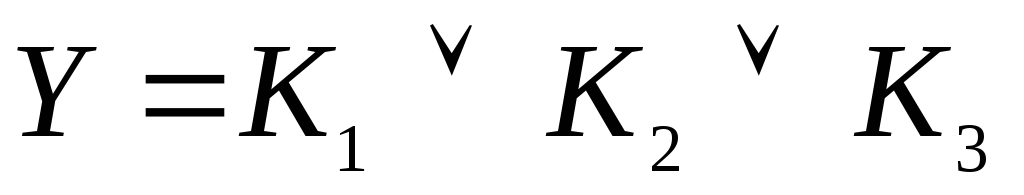
(5)

Подставляем в (5) значения конечных конъюнкций из (2), (3) и (4) получаем формулу МДНФ:

(6)

6. Проверка мднф с помощью импликантной матрицы.

Формула МДНФ (6) может оказаться не минимальной и содержать ошибки. Для проверки строится импликантная матрица (таблица 4) следующим образом:

Исходные конъюнкции (ИК) располагаются в столбцах:

(1)

Конечные конъюнкции (КК) располагаются в строках:

(6)

Если конечная конъюнкция поглощает исходную конъюнкцию, то на пересечении строки и столбца ставится знак «+».
Если знак «+», оказался единственным в столбце, то он обводится кружком «». Все знаки «+», выбранной строки, также обводятся кружками. Конечная конъюнкция, относящаяся к этой строке, 6вляяется обязательной.
Если все, не обведенные знаки «+» конечной конъюнкции дублируют обведенные знаки «+» в столбцах, то данная конечная конъюнкция является избыточной (лишней).