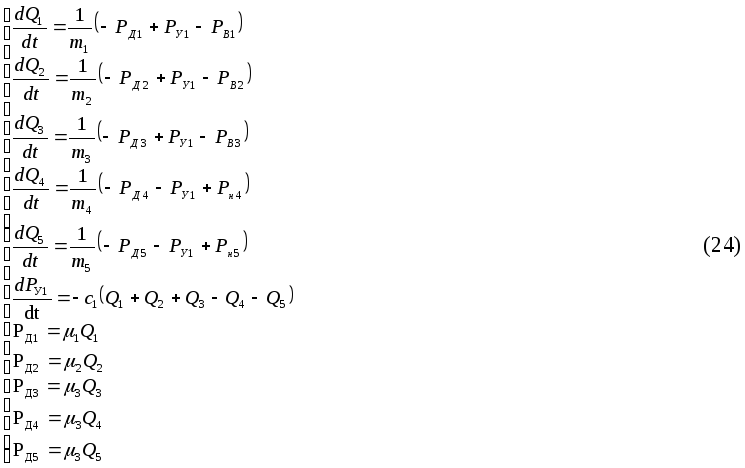СОДЕРЖАНИЕ

3

4

4

5

Введение

1 Моделирование на микро уровне

1.1 Микрофон: принцип работы и классификация

1.2 Выбор уравнения и его идентификация

1.3 Расчет статической характеристики 9

1.4 Расчет динамической характеристики 13

1.5 Моделирование мембраны в среде Matlab 15

2 Моделирование на макро уровне 16

2.1 Исходные данные 16

2.2 Графические формы математической модели гидросистем 18

2.2.1 Динамическая схема 18

2.2.2 Орграф 18

2.2.1 Матрица инциденций 19

2.3 Узловой метод формирования математической модели

гидросистемы 19

2.4 Расчет статической модели гидросистемы 20

2.4.1 Вычисление параметров трубопровода гидросистемы 23

2.4.2 Результаты статического анализа 25

2.5 Анализ динамической модели гидросистемы 25

2.5.1 Выбор шага интегрирования 27

2.5.2 Решение систем дифференциальных уравнений методом Эйлера 28

Заключение 29

Список использованной литературы 30

Приложение 31

ВВЕДЕНИЕ

Основной характеристикой СРП является континуальная передаточная функция. Она показывает отношение выходной функции к выходной (по Лапласу) в привязке к конкретной точке.

Одним из примеров СРП могут служить т.н. «длинные линии», изучаемые в курсе электротехники, т.е. проводники, размеры которых сопоставимы с длиной волны, а электрические параметры (сопротивление, емкость и индуктивность) распределены по всей длине.

Математически СРП описываются дифференциальными уравнениями в частных производных, также для этого вводятся функции Грина, континуальная и интегральная передаточные функции.

Система с сосредоточенными параметрами (ССП) является частным случаем СРП и вводится для упрощения и решения задач на первом этапе. В большинстве случаев такого упрощения оказывается достаточно для получения адекватных результатов, но в ряде задач распределение параметров в пространстве оказывает существенное воздействие на результаты, в этом случае применяется аппарат теории СРП.

В искомой задаче выходная функция обозначается Q(x,t), где х – трехмерная переменная в декартовых, полярных, цилиндрических или сферических координатах, f(x,t) – входная координата по среде, зависящая от трехмерной координаты х и t.

Основное уравнение задачи записывается в виде:

где L –оператор дифференциального уравнения – формула преобразования выходной величины Q.

В каждой задаче определяются граничные или краевые условия

где Г – оператор граничных или краевых условий.

g – входное воздействие на границе в каждый момент времени.

Для того, чтобы решить задачу во всей области координат, необходимо знать ее значения в каждой точке по границе области.

Начальные условия для задачи записываются в виде:

где N – оператор начальных условий;

Q₀(x) – значение искомой функции в заданный момент времени t₀ в каждой точке пространства x.

Получили систему:

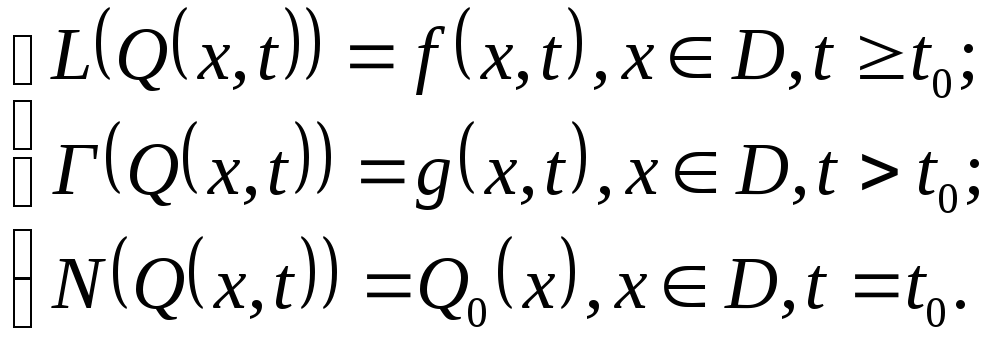(1)

Необходимо знать:

1. Значение функции на границе в каждый момент времени.

2. Значение в каждой точке области в момент времени t₀.

В указанном виде (1) система практически не разрешима. Для ее решения вводится в рассмотрение стандартная форма записи (1). Она подразумевает нулевые граничные и начальные условия. Ее вид:

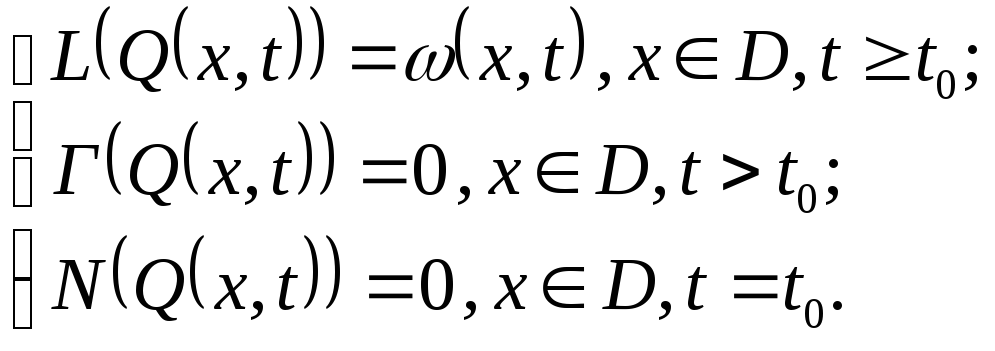(2)

где (x,t) – стандартизующая функция (x,t)= f(x,t)

При Г=0, N=0 – входное воздействие на систему при нулевых граничных и начальных условиях и первая из трех основных функций, которая понадобится при решении (берется из справочника).

Второй функцией является функция Грина (импульсная переходная функция, функция влияния, функция источника, функция веса).

Функцией Грина называется функция источника, которая равна выходному сигналу G(x,t)=Q(x,t) при f(x,t)=δ(x-ξ)·δ(t-τ), где δ(x-ξ) – пространственная δ функция по координатам х,y,z δ(t-τ)-функция по времени; х – координата входного возмущения; ξ – координата точки отклика о удара.

С учетом этого стандартная задача (2) перепишется в виде:

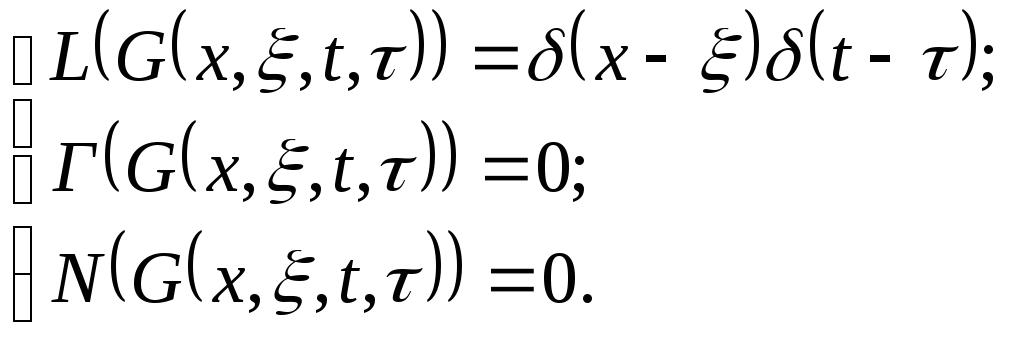(3)

где функция Грина от G(x,t) берется из справочника и является второй основной характеристикой.

Зная эти две характеристики можно найти выходную функцию по следующему выражению:

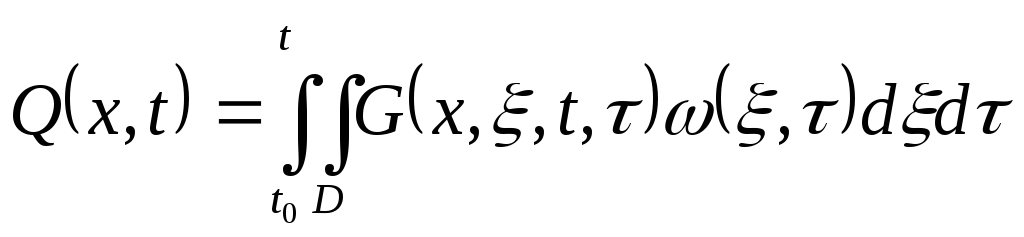(4)

Если задача статическая, то есть отсутствует уравнение времени t, то ее можно записать в виде:

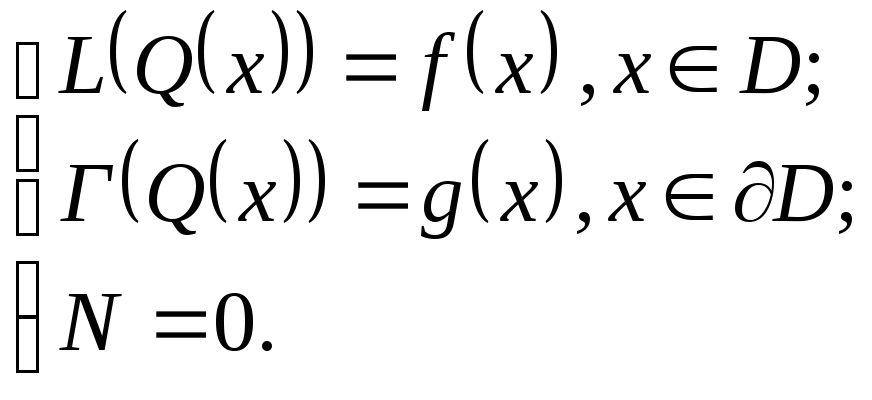(5)

Стандартная форма записи будет выглядеть в виде:

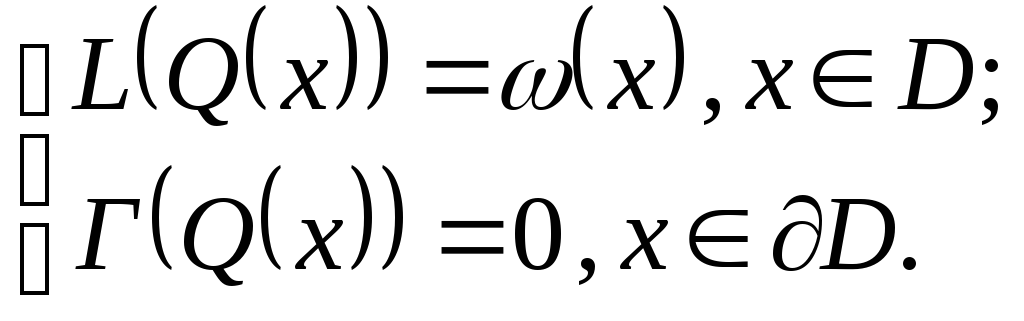(6)

при однородных (нулевых) граничных условиях.

Функция Грина такой задачи удовлетворяет системе уравнений:

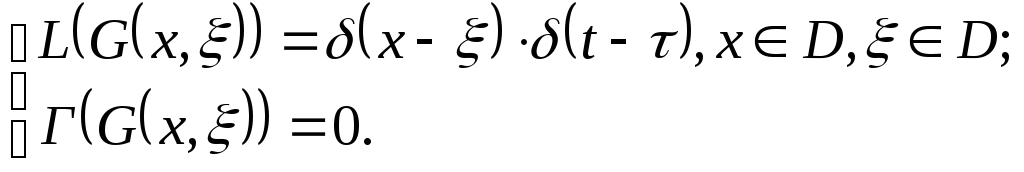(7)

x – координаты возмущения;

 - координаты отклика.

Решение задачи в этом случае выглядит следующим образом:

(8)

Бывают задачи, в которых отсутствуют пространственные координаты, т.е. процесс во времени. В таком случае задача записывается следующим образом:

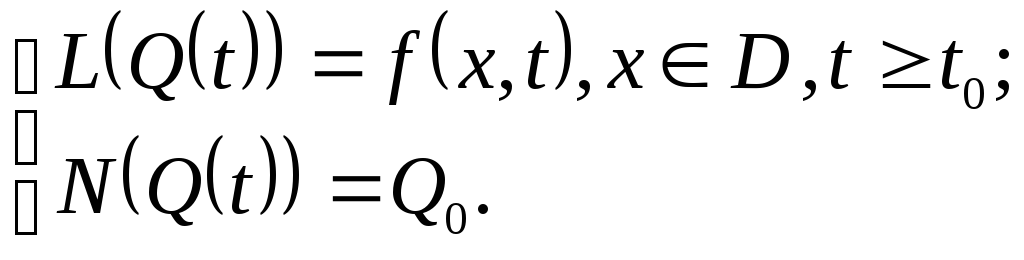(9) Стандартная форма записи:

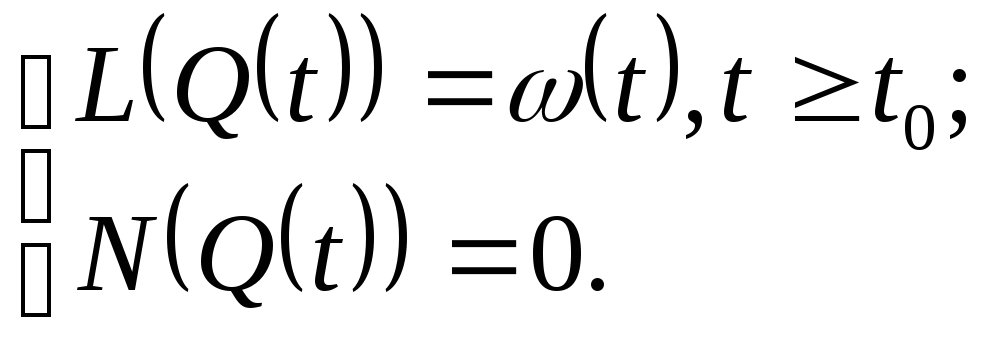(10)

Функция Грина:

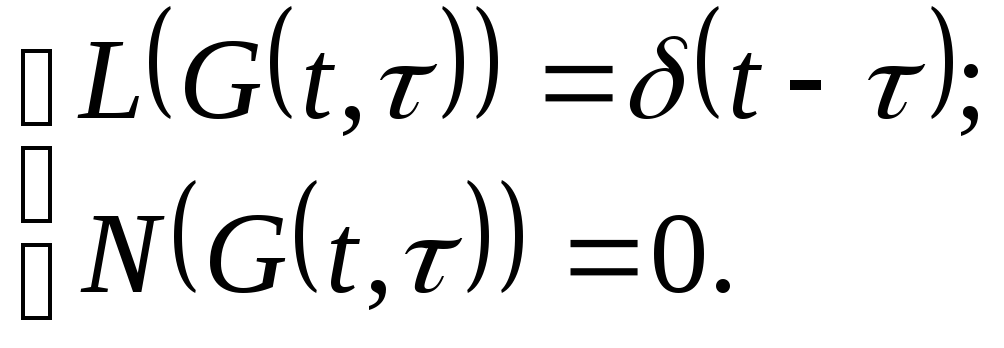(11)

Решение такой задачи имеет вид:

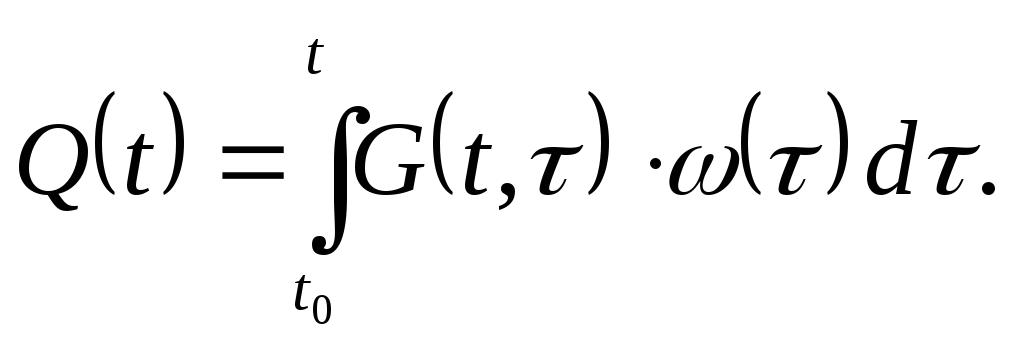(12)

Таким образом, для решения этой задачи принципиально достаточно трех формул (4),(8),(12), то есть по двум справочным функциям (нормирующей и Грина) можно всегда определить выходную функцию Q.

Для управления и синтеза системы управления, исходя из ТАУ, необходимо знать передаточную функцию. В теории СРП вводится понятие континуальной передаточной функции, т.е. точечной передаточной функции, в пределах области D, когда возмущение подается на среду в точке x функциями: δ(x-ξ) и δ(t-τ), а реакция регистрируется в точке .

Континуальная передаточная функция выражается следующим образом:

. (13)

По сути, континуальная передаточная функция – это преобразование Лапласа функции Грина, т.е. при этих функциях континуальная передаточная функция является производной и всегда может определиться по функции Грина.

Таким образом, для решения задачи по СРП необходимо знать две функции: нормирующую функцию и функцию Грина.

Теория СРП включает структурный метод ТАУ, который подразумевает операции с распределенными блоками:

1. блоки соединяются последовательно;

2. блоки соединяются параллельно;

3. включение второго блока в обратную связь.

В связи с этим вводится понятие операторного изображения выходной величины. В теории распределенных блоков выходная величина определяется следующим образом:

, (14)

где - изображение по Лапласу выходной величины решаемой задачи;

- континуальная передаточная функция;

- изображение по Лапласу нормирующей функции.

Если удается из нормирующей функции ω(ξ,p) выделить в явном виде компоненту входной координаты с помощью специальных средств или методов

, (15) (то уравнение (14) перепишется в виде:

(16)

С помощью двух способов (коэффициент разложения и коэффициент приближения) по возможности выносится входное возмущение (по Лапласу) за знак интегрирования, получим:

(17)

Полученное выражение (17) – отношение изображения по Лапласу выходной величины к изображению по Лапласу входного возмущения, как интеграл по области D континуальных функций, называется интегральной передаточной функцией (функция Власова В.В.).

Разделяя полученное выражение на действительную и мнимую части и используя формулу:

; (18)

строим график ЛАЧХ, аппроксимируем ее с погрешностью 5 % типовыми звеньями и запишем выражение аппроксимированной передаточной функции.

1 МОДЕЛИРОВАНИЕ НА МИКРО УРОВНЕ

1.1 Исходные данные

Исследуется колебание струны l =1м., закрепленной в одной точке.

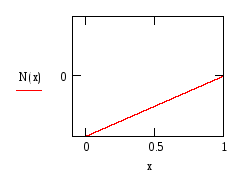
(а) (б)

Рис.1 (а) - изображение струны, (б) – граничные условия

начальные условия:, ;

граничные условия: ;

Входное воздействие f(x,t)=0

Стандартизирующая функция:

Функция Грина:

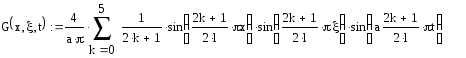
Континуальная передаточная функция:

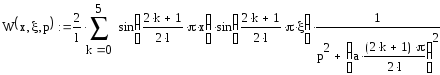
1.2 Выбор уравнения и его идентификация

Рассмотрим процесс колебания струны и проведем его идентификацию выходной величины Q и коэффициента а.

Q(x,t)=(м)

1.3 Расчет статической характеристики

Идентификация исходного уравнения позволяет перейти к расчету распределенной выходной величины, являющейся функцией как пространственной, так и временной координаты.

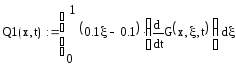
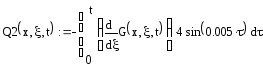
Подставим в уравнение а=1 и l=1, то есть ограничим длину струны величиной в 1м.

Первая составляющая решения выходной функции:

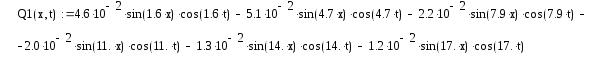
Вторая составляющая решения выходной функции:

Выходная величина

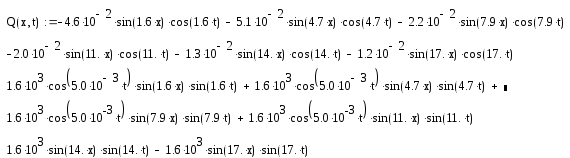
Построим график этой функции при фиксированном t

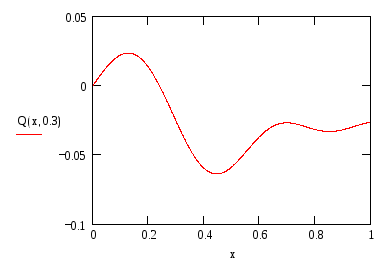
• Рисунок 1.2 – График выходной величины Q(x,t) при t=0.3

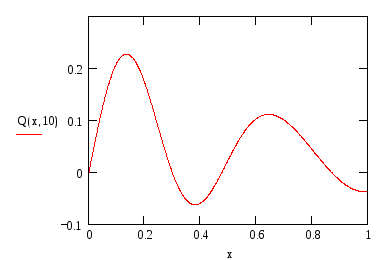
• Рисунок 1.3 – График выходной величины Q(x,t) при t=10

1.4 Расчет динамической характеристики

Динамическая характеристика находится по интегральной передаточной функции, которая рассчитывается как пространственная композиция от произведения континуальной передаточной функции и от преобразованной по Лапласу стандартизирующей функции с выделенным из нее входным воздействием:

(16)

Найдем изображение стандартизирующей функции по Лапласу:

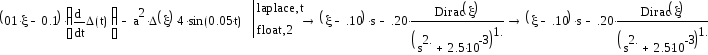
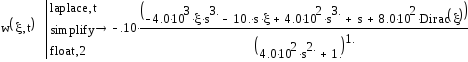
Интегральная передаточная функция запишется в виде:

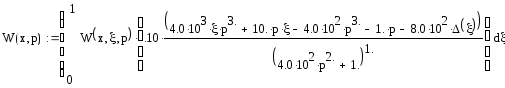
Подставим в выражение исходные данные и ограничим величину х=1

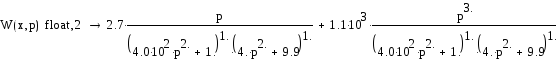
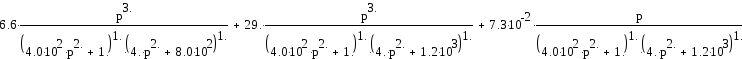
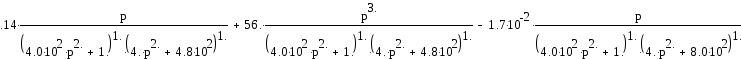
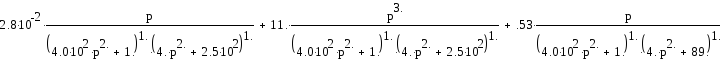
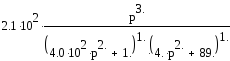
При замене р на jω последнее выражение примет вид:

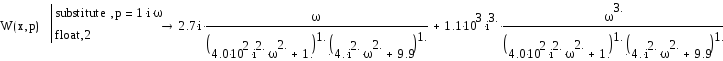
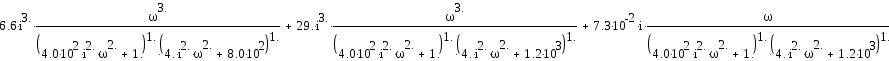
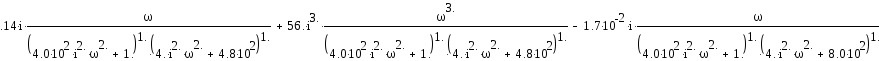
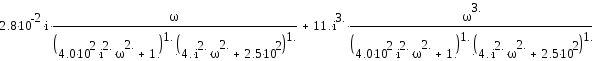
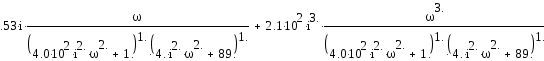
Выделим действительную и мнимую части

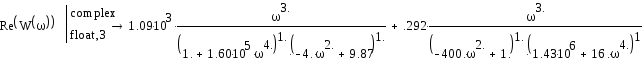
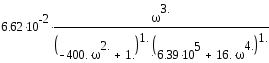
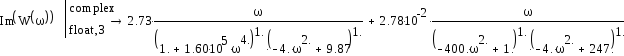
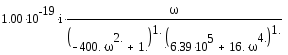
Для выбранной выходной переменной построим ЛАЧХ.

Найдем ЛАЧХ по выражению:

(20)

Для построения характеристики используем программу MathCad.

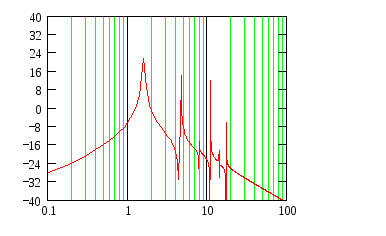
Р

ω

L(ω)

исунок 4 – Логарифмическая амплитудно-частотная характеристика

Полученная ЛАЧХ представлена на рисунке 4. Аппроксимируем ее стандартными типовыми наклонами. Получаем интегрирующее и апериодическое звено с собственной частотой ω= Гц. Тогда передаточная функция имеет вид:

Из ЛАЧХ можно сделать вывод, что усиление равно:

20lgk= – 8 k=0.4 (21)

С помощью аппроксимации передаточная функция запишется в виде:

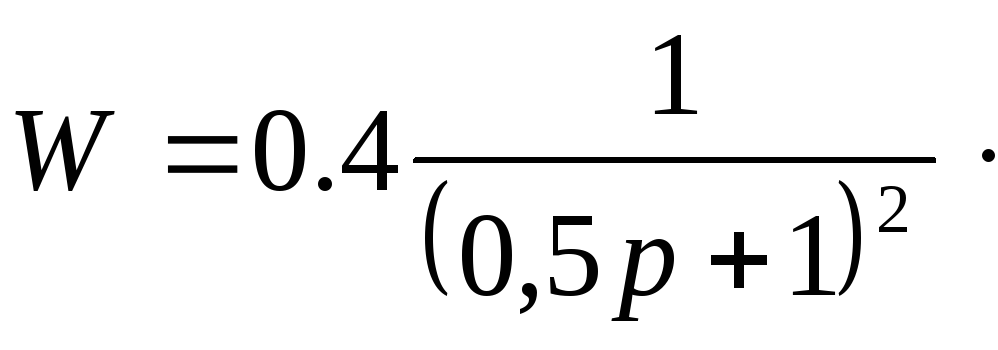
1.5. Моделирование струны в среде Matlab

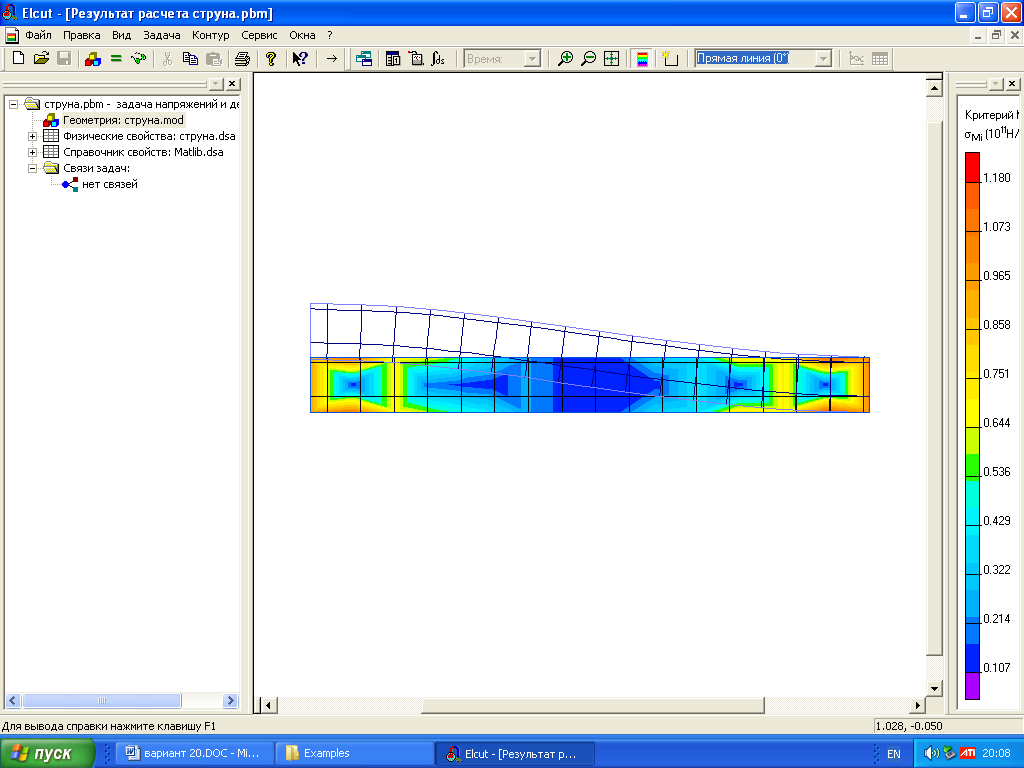
Рисунок 5 – Моделирование перемещения центра мембраны от начального положения.

2 МОДЕЛИРОВАНИЕ НА МАКРОУРОВНЕ

2.1 Исходные данные

Дана схема гидравлической системы, представленная на рисунке 7. В системе используется в качестве рабочей жидкости вверенное масло АУ. Материал трубопровода – латунь. Основные параметры системы и жидкости приведены в таблице 1. Параметры трубопроводов приведены в таблице 2.

P_B2

P_B3

Qn1

Qn2

P_B1

Рисунок 7 – Схема гидравлической системы

1, 2, 3 - магистрали потребителей; P_B1, P_B2, P_B3 - давление потребителей; Q_H – насос.

Таблица 1 – Параметры системы и жидкости

Обозначение	Основные параметры	Значение
	Плотность рабочей жидкости	860 кг/м3
	Вязкость	0,15·10-4 м2/с
ЕС	Модуль упругости системы	1,7·108 Па
Етр	Модуль упругости трубопровода	9*1010 Па
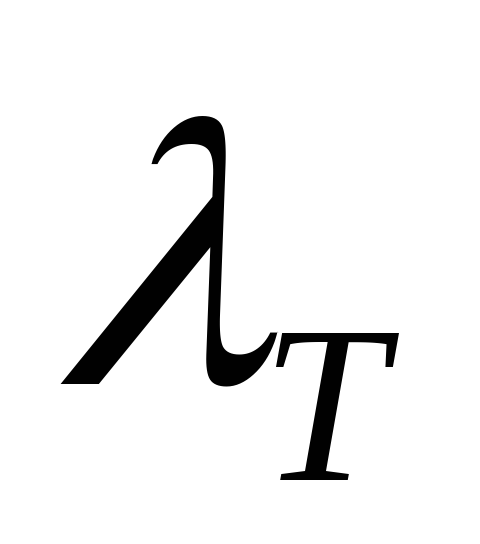
	Коэффициент потерь на трение при турбулентном потоке	0,028
	Толщина стенки трубопровода	0,3мм

^{Таблица 2 – Параметры трубопроводов}

Параметр	Обозначение	Номер трубопровода
		1	2	3	4	5
Диаметр трубопровода	dтр, м	0,015	0,15	0,01	0,02	0,015
Длина трубопровода	l,м	1,5	1	2	0,55	0,5
Коэффициент местных сопротивлений	ξ	5	3	5,5	2	1,5
Давление потребителей и насосов	P, *106 Па	0,1	0,15	0,2	-	-

Q_n1 = 0*10^-6 м³/с;

Q_n2 = 400*10^-6 м³/с.

2 Графические формы математической модели гидросистемы

2.2.1 Динамическая схема. На основании исходной принципиальной схемы гидравлической системы строится динамическая модель. Участки магистралей представляются как последовательное соединение инерционного и диссипативного элемента, причем для инерционного элемента указывается направление движения рабочей жидкости. Инерционными элементами называются сосредоточенные мамы, обладающие инерционными свойствами и способностью накапливать кинетическую энергию. Диссипативные элементы отображают свойства диссипации (рассеивания) энергии конструктивными элементами технического объекта, обусловленные силами внутреннего трения. В точки ветвления магистралей устанавливают упругие элементы, учитывающие сжимаемость жидкости и деформируемость стенок трубопровода. На рисунке 8 представлена полученная динамическая модель.

2.2.2 Орграф. На основании динамической модели построен ориентированный граф, являющийся графической формой модели гидравлической системы. Узлы орграфа соответствуют сосредоточенным массам, а ветви – компонентам математической модели. Базовый узел (с нулевым номером) отображает инерциальную систему отсчета фазовых координат типа потока. Источник обеспечивает возрастание потоковой переменной узла, поэтому сигналы направляют от базы к узлу. В магистралях потребителей – наоборот. Во всех ветвях инерционных и диссипативных элементов направление сигналов от узла к базе. Такое направление характеризует затраты энергии источников на увеличение кинетической энергии и на трение. В ветвях упругих компонентов стрелки указывают направление передачи энергии от источников к потребителям. В ветвях всех элементов кроме направления записывается параметр каждого элемента. На рисунке 9 представлен полученный орграф.

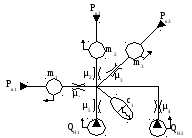
Рисунок 8 – Динамическая модель гидравлической системы

С₁

С₁

С₁

2

С₁

m₂

Pв₁ Pв₂ 3

1 µ₂ µ₃ С₁

С₁ m₁ m₃

µ₁ Рв₃

µ₄ µ₅

4 5

Рн₁ Рн₂

Рисунок 9 – Ориентированный граф гидравлической системы

2.2.3 Матрица инциденций. Для формирования полной математической модели на основе компонентных и топологических уравнений широкое применение получил узловой метод, для него необходимо сформировать матрицу инциденции, отражающую структуру связей всех элементов системы. Матрица инциденции формируется на основании ориентированного графа. Число строк матрицы соответствует числу узлов орграфа, число столбцов – числу ветвей. Отсутствие связи между узлом и ветвью обозначается «0», если ветвь входит в узел – «1», если выходит – «-1».

Матрицу инциденции А можно представить состоящей из подматриц инерционных А_И, диссипативных А_Д, упругих А_У ветвей и подматрицы ветвей источников потенциалов А_В. Для исходной системы получена матрица, представленная в таблице 3.

А=[A_И, А_Д, А_У, А_В] (22)

Таблица 3 – Матрица инциденций гидравлической системы

Узлы	Ветви
	Диссипативные узлы					Упругие	Внешнее воздействие
	µ1	µ2	µ3	µ4	µ5	С1	Рв1	Рв2	Рв3	Рн1	Рн2
1	-1	0	0	0	0	1	-1	0	0	0	0
2	0	-1	0	0	0	1	0	-1	0	0	0
3	0	0	-1	0	0	1	0	0	-1	0	0
4	0	0	0	-1	0	-1	0	0	0	1	0
5	0	0	0	0	-1	-1	0	0	0	0	1
	Ав					Ау	Ад

2.3 Узловой метод формирования математической модели гидросистемы

Из матрицы инциденций можно получить систему равнений (23), математически описывающие гидравлическую систему.

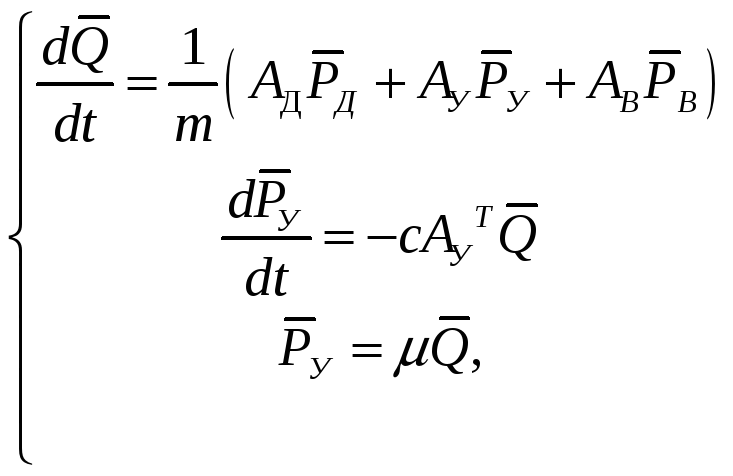(23)

где А_Д, А_У, А_В – подматрицы инциденций,

- векторы давлений,

- векторы расходов,

m, с, - диагональные матрицы параметров элементов гидравлической системы.

Для нашего случая система будет иметь вид: