1.4 Частотная характеристика конденсаторного микрофона.

Если исключить из рассмотрения очень низкие частоты. То поведение конденсаторного микрофона характеризуется прежде всего резонансом системы напряженная мембрана – задняя полость (объём воздуха позади мембраны мал). Эквивалентная электрическая схема при этом упрощается до последовательной резонансной схемы, представленной на рисунке 5,б.

С использованием упрощенных обозначений.

M=M_A+M_D+M_S, C=C₂C_D/(C₂+C_D)

Уравнение для тока Au = U_D принимает вид

Mjωu +Ru +u/(jωC)=p/A

Отметим, что для микрофонов с сильно напряжённой металлической мембраной С~С_D, и выходное напряжение определяется выражением

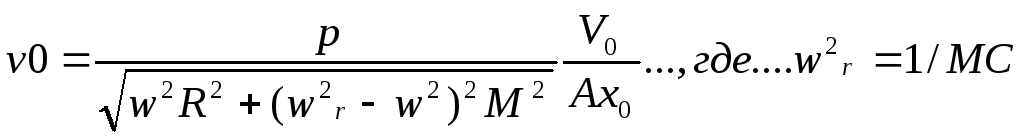
В зависимости от величины ω на частотной характеристике можно выделить следующие области (рис 6)

- при частоте ниже резонансной ω<<ω_r

И сигнал не зависит от ω (зона II)

- при резонансной частоте ω = ω_r

Рисунок 6 Частотная Характеристика конденсаторного микрофона.

- при частоте выше резонансной ω>ω_r

и сигнал ослабляется на 12 дБ/октава (зона IV).

При более высоких частотах теоретически должен существо­вать антирезонанс параллельного контура, включающего M_s и С₁ (область V), и, кроме того, резонанс последовательного контура, образуемого M_A + M_D и емкостями C_D и С₁ т. е. вто­рой резонанс микрофона, создаваемый мембраной и полостью, расположенной позади диафрагмы (зона VI). В реальных мик­рофонах эффекты дифракции играют доминирующую роль.

При очень низких частотах (f<<l/2πRC_T) к влиянию капил­лярного канала (ослабление 6 дБ/октава, зона I, f<<l/2πRC₂) может добавляться электронный эффект, вызванный непостоян­ством заряда. Подобный эффект, описанный Дёбелином, про­являлся в дополнительном ослаблении сигнала 6 дБ/октава.

1.5 Получение передаточной функции

Выведем передаточную функцию для эквивалентной электрической схемы конденсаторного микрофона показанной на рисунке 7

Рисунок 7 Эквивалентная электрическая схема конденсаторного микрофона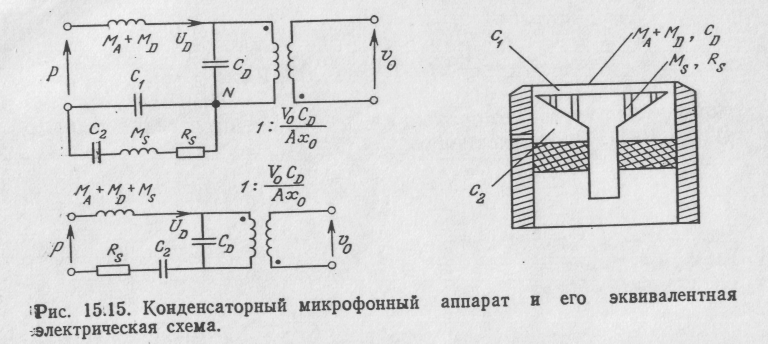

Запишем уравнения по законам Кирхгофа и Ома в операторной форме:

Произведём формальную замену L=M_A+M_D+M_S

Для первого контура:

p+U_L+U_CD+U_C2+U_RS=0

(1)

Или в изображении по Лапласу

(2)

Для второго контура:

-U_CD+U_L1-U_M=0

(3)

Или в изображении по Лапласу

(4)

Для третьего контура:

-U₀+U_L2-U_M=0 →U₀=U_М-U_L2

(5)

Или в изображении по Лапласу

(6)

По первому закону Кирхгофа

i₁ = i₂ - i₄ = 0

I₄(S)=I₁(S) – I₂(S)

Из 2

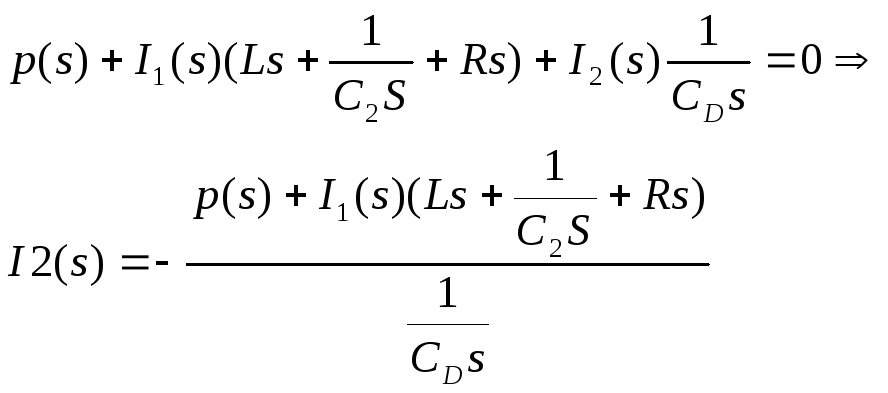(7)

Подставим 7 в 4

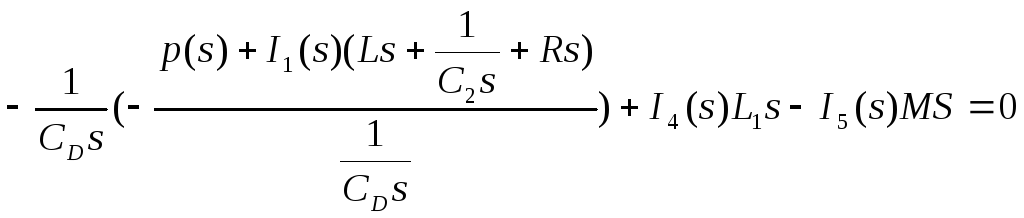
(8)

Из 8

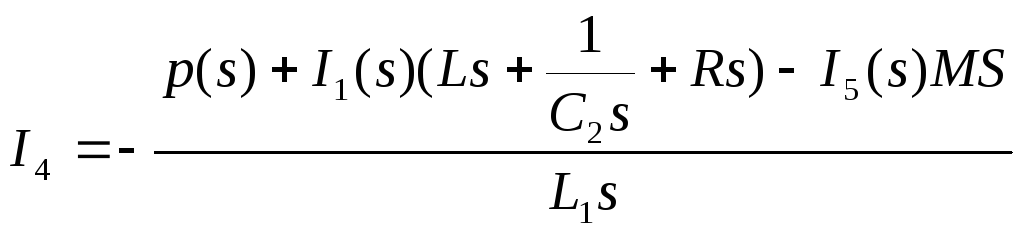(9)

Подставим 9 в 6

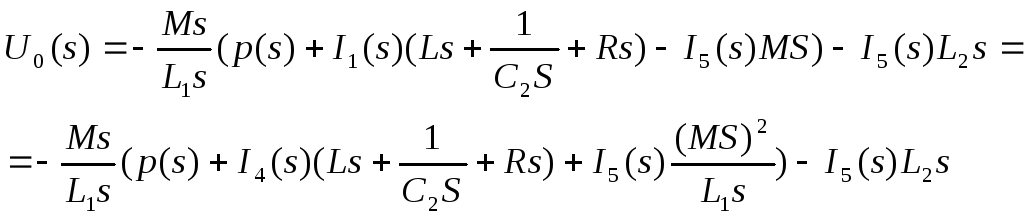
Те

Т.к количество переменных больше количества уравнений в системе, то система является недоопределённой и вывести по данным условиям передаточную функцию не представляется возможным.

2 Представление устройства в виде структурной схемы

Представим устройство емкостного датчика в виде функциональной схемы, т.е. последовательности блоков, представляющих собой системы с распределёнными (СРП) или сосредоточенными параметрами (ССП).

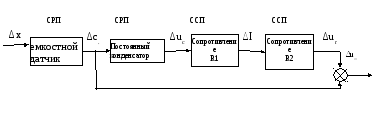
Рисунок 3

Здесь ∆x – измеряемое перемещение;

∆c_.. – изменение емкости постоянного конденсатора;

∆u_c– изменение напряжения на конденсаторе;

∆I– изменение протекаемого тока;

∆u_r – изменение напряжения на сопротивлениях;

∆u_m– напряжение разбаланса.

Представим устройство емкостного датчика в виде структурной схемы.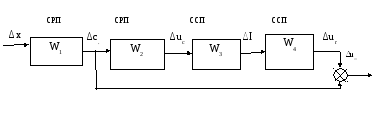

Рисунок 4

Здесь W₁ – W₄ – передаточные функции соответствующих блоков функциональной схемы (рисунок 3).