СОДЕРЖАНИЕ

Введение 3

1 Моделирование на микроуровне 5

1.1 Основные понятия СРП 5

1.2 Выбор уравнения и его идентификация 7

1.3 Расчет функции распределения 9

1.4 Расчет интегральной передаточной функции. Построение ЛАЧХ 11 12

1.5 Моделирование в Elcut 13

2 Моделирование на макроуровне 14

2.1 Исходные данные 14

2.2 Графические формы математической модели 15

2.3 Узловой метод формирования математической модели 18

2.4 Анализ статической модели 21

2.5 Анализ динамической модели 25

Заключение 32

Список используемых источников 33

Приложение А 34

ВВЕДЕНИЕ

Модель – физический или абстрактный образ моделируемого объекта, удобный для проведения исследований и позволяющий адекватно отображать интересующий исследователя физические свойства и характеристики объекта.

При проектировании технических объектов используют множество видов математических моделей в зависимости от уровня иерархии, степени декомпозиции системы, стадии и этапа проектирования на любом уровне иерархии объект представляют в виде некоторой системы, состоящей из элементов.

В зависимости от степени абстрагирования различают три основных иерархических уровня: верхний (метоуровень), средний (макроуровень), нижний (микроуровень).

Метоуровень соответствует начальным стадиям проектирования. Для построения математической модели метоуровня используют методы математической логики, теории графов и т.п.

На макроуровне объект проектирования рассматривают как динамическую систему с сосредоточенными параметрами. ММ макроуровня представляет собой систему обыкновенных дифференциальных уравнений.

На микроуровне объект представляется как сплошная среда с распределенными параметрами. Для описания процесса функционирования таких объектов используют дифференциальные уравнения в частных производных. На микроуровне проектируют неделимые по функциональному признаку элементы технической системы, называемые базовыми элементами.

Цель данной курсовой работы заключается в исследовании объекта на микроуровне и расчёта гидравлической системы на макроуровне.

1 Моделирование на микроуровне

1. Основные понятия срп

Основной характеристикой СРП является континуальная передаточная функция. Она показывает отношение выходной функции к входной (по Лапласу) в привязке к конкретной точке.

В искомой задаче выходная функция обозначается буквой Q(х,t), где x - трехмерная переменная в декартовых, полярных, цилиндрических или сферических координатах, f(x,t) - входная координата по среде, зависящая от трехмерной координаты х и времени t. Основное уравнение задачи записывается в виде:

L(Q(х,t)) = f(х,t), xD, t>t₀,

где L - оператор дифференциального уравнения - формула преобразования выходной величины Q;

D - открытая пространственная область.

В каждой задаче определяются граничные или краевые условия:

Г(Q(х,t))=g(х,t);x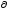D,t>t₀,

где Г - оператор граничных или краевых условий, g - входное воздействие на границе в каждый момент времени;

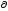D - граница пространственной области, то есть необходимо знать ее значения в каждой точке по границе области в момент времени t>0.

Начальные условия для задачи записываются в виде:

N(Q(х,t))=Q₀(х); x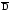, t=t₀,

где N - оператор начальных условий;

Q₀(х) - значение искомой функции в момент времени;

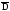- закрытая пространственная область, содержащая начальные границы.

Получили систему:

l(Q(х,t)) = f(х,t), xD, t>t₀,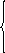

Г(Q(х,t))=g(х,t);x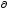D,t>t₀,

N(Q(х,t))= Q₀(х); x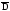, t=t_0.

Данная система практически не разрешима. Для ее решения вводится в рассмотрение стандартная форма записи. Она подразумевает нулевые граничные и начальные условия. Её вид:

l(Q(х,t)) =ω(х,t), xD, t>t₀,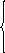

Г(Q(х,t))=0;x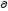D,t>t₀,

N(Q(х,t))=0; x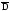, t=t₀,

где ω(х,t) - стандартизующая функция.

Для решения краевой задачи в стандартной форме используется функция Грина. Функцией Грина называется функция источника, которая равна выходному сигналу G(x,t) = Q(x,t) при входном воздействие в виде:

f(х,t)= δ(х - ξ) δ(t - τ)

где δ(х - ξ) - пространственная δ-функция по координатам x,y,z;

δ(t - τ) - функция по времени;

ξ - координаты входного возмущения;

х - координаты точки отклика от удара.

С учетом этого стандартная задача перепишется в виде: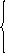

l(G(х,ξ,t,τ)) = δ(х - ξ) δ(t - τ),

Г(G(х, ξ,t,τ))=0,

N(G(х, ξ,t,τ))=0;

Зная эти две характеристики можно найти выходную функцию:

,

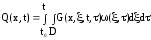Для управления и синтеза системы управления, исходя из ТАУ, необходимо знать передаточную функцию. В теории СРП вводится понятие континуальной передаточной функции, то есть точечной передаточной функции в пределах области D, когда возмущение подается на среду в точке ξ, а реакция регистрируется в точке х.

Континуальная передаточная функция выражается следующим образом:

,

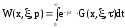Теория СРП включает структурный метод ТАУ, который подразумевает операции с распределенными блоками: если блоки соединяются последовательно; если блоки соединяются параллельно; при включении второго блока в обратную связь. В связи с этим вводится понятие операторного изображения выходной величины. В теории распределенных блоков выходная величина равна:

,

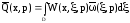где 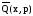- изображение по Лапласу выходной величины решаемой задачи;

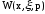- континуальная передаточная функция;

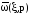- изображение по Лапласу нормирующей функции.

Если удается из нормирующей функции 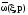выделить в явном виде компоненту входной координаты с помощью специальных средств или методов

,

,

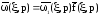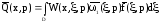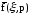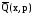Если вынести входное возмущение за знак интеграла и разделить на него выходную величину , то получим:

,

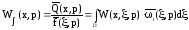Полученное выражение - отношение изображения по Лапласу выходной величины к изображению по Лапласу входного возмущения.

Целью работы является расчет выходной распределенной величины 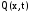и интегральной передаточной функции .
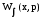