курсовая работа / КР МСУ 5-й курс

СОДЕРЖАНИЕ

Введение 3

1 Моделирование на микроуровне 5

1.1 Исходные данные 5

1.2 Идентификация краевой задачи 5

1.3 Расчет выходной распределенной величины 8

1.4 Расчет интегральной передаточной функции 12

1.5 Построение логарифмической амплитудно-частотной

характеристики 14

Заключение 14

Список использованных источников 15

ВВЕДЕНИЕ

Моделирование – процесс замещения объекта исследования некоторой его моделью и проведение исследования на этой модели с целью получения необходимой информации об объекте.

Модель – физический или абстрактный образ моделируемого объекта удобного для проведения исследований и позволяющий адекватно отображать интересующие исследователя физические свойства и характеристики объекта.

Различают моделирование предметное и абстрактное.

При предметном моделировании строят физическую модель, которая соответствующим образом отображает физические свойства объекта, при этом объект может иметь иную физическую природу. Недостаток такого вида моделирован - большие временные и материальные затраты.

Абстрактное моделирование связано с построением абстрактной моде (математические соотношения, графы, схемы, диаграммы). Наиболее мощным средством абстрактного моделирования является математическое моделирование.

Математическое моделирование позволяет посредством математических символов и зависимостей составить описание функционирования технического объекта в окружающей внешней среде, определить выходные параметры и характеристики, получить оценку показателей эффективности и качества, осуществить поиск оптимальной структуры и параметров объекта.

Математическая модель - совокупность математических объектов и отношений между ними, адекватно отображающих физические свойства объекта.

В зависимости от степени абстрагирования различают 3 основных иерархических уровня: верхний (меттауровень), средний (макроуровень), нижний (микроуровень).

На микроуровне объект представляется как сплошная среда с распределенными параметрами. Для описания процесса функционирования таких объектов используют дифференциальные уравнения в частных производных. На микроуровне проектируют неделимые по функциональному признаку элементы технической системы, называемые базовыми элементами (вал, мембрана, стержень).

Целью курсовой работы является синтез интегральной передаточной функции для объектов управления с распределенными параметрами. В данной работе решается вопрос построения математической модели нагрева диска на основе теории распределенных сигналов: по заданному дифференциальному уравнению объекта получить выражение для передаточной функции в распределенных параметрах, выражение для выходной величины, выражение для оценочной передаточной функции для наилучших условий управления. Построить оценочную ЛАЧХ, аппроксимировать ее и записать выражение передаточной функции через типовые звенья. Кроме того на макро-уровне необходимо исследовать статическую и динамическую модель гидросистемы. Для чего необходимо составить систему дифференциальных уравнений статической модели методом Ньютона, а динамическую модель рассчитать методом Эйлера. В итоге необходимо построить переходный процесс системы.

1 МОДЕЛИРОВАНИЕ НА МИКРОУРОВНЕ

1.1 Исходные данные

В качестве исходных данных для моделирования на микроуровне примем следующие (Бутковский, стр. 64 нижнее)

Дифференциальное уравнение:

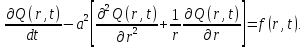(1.1)

Входное воздействие:

f(r,t)=0. (1.2)

Начальные условия:

Q(r,0)=Q­₀(r)=Ar²+B. (1.3)

Граничные условия:

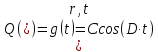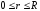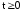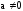_, , , _{. (1.4)}

Стандартизирующая функция:

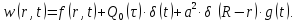(1.5)

Функция Грина:

G(r,ρ,t)= 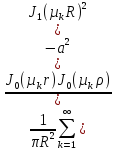, (1.6)

где μ_k – расположенные в порядке возрастания положительные корни уравнения.

J₀(μR)=0. (1.7)

_{Континуальная} передаточная функция:

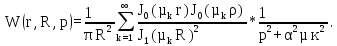(1.8)

1.2 Идентификация краевой задачи

Уравнение (1.1) представляет собой параболическое уравнение. Содержит первую производную по времени t и вторую производную по r. Данное уравнение описывает нагрев диска. Проведём идентификацию всех величин входящих в уравнение (1.1).

Дифференциальное уравнение имеет вид:

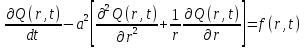_, (1.9)

где Q(r,t) – выходная распределённая величина, представляющая собой температуру ^оС;

f(x,t) – внешнее воздействие.

Для уравнения (1.1) формулируются следующие условия:

- начальные условия: ,

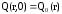- граничные условия: Q(R,t)=g(t)=Ccos(D·t), , , _.

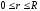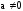Стандартизирующая функция, компенсирующая влияние начальных и гра­ничных условий для данной задачи имеет вид (1.5).

Функция Грина, являющаяся решением краевой задачи при начальных и гра­ничных условиях и входном воздействии в виде δ-функции имеет вид (1.6).

Континуальная передаточная функция, являющаяся преобразованием Лап­ласа функции Грина имеет вид (1.8).

Для решения частной задачи примем следующие условия:

- начальные условия, описывающие температуру в начальный момент времени:

_Q(r,0)=Q₀(r)=A·r+B=0.2·r+3; (1.10)

- граничные условия, описывающие температуру на концах радиуса диска:

Q(R,t)=g(t)=Ccos(D·t)=5·cos(0.25t)+10, (1.11)

, , _.

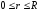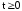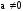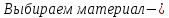бетон, плотность которого равна ρ=2*10³ [кг/м³], радиус диска R=10 м.

Найдем размерность а – коэффициент температуропроводности материала.

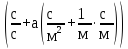.Таким образом а=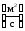

Коэффициент температуропроводности ,

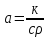где К - коэффициент теплопроводности K=1,33 [];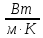

С=980 - удельная теплопроводность вещества (Дж/кг·к);

а²=4,7·10^-13 [м²/с].

Представим на рисунке 1 изображение диска в начальный момент времени:

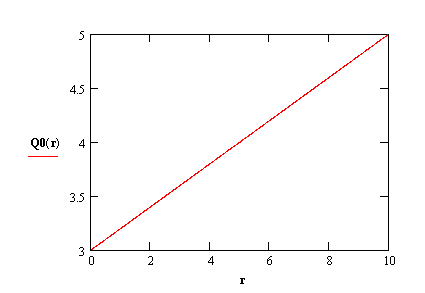
Рисунок 1 – Изображение температуры диска в начальный момент времени

Отобразим на рисунке 2 граничное условие на конце диска:

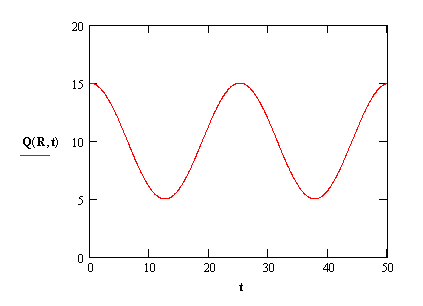
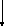
Рисунок 2 –Температура диска на радиусе R

Q(0,t)=g(t)=C·sin(D·t)=5·sin(0.25*t) +10 (1.12)

С учётом входного воздействия, принятых начальных и граничных условий стандартизирующая функция принимает вид:

ω(r,t)=(2r²+0,3)δ(t)+4.7·10^-13δ`(10-r)·5cos(0.25t)+10 (1.13)

где δ(t) и δ`(10-r) – импульсные функции.

1.3 Расчёт статической характеристики

Зная стандартизирующую функцию и функцию Грина, можно найти выходную функцию, вычислением интеграла, представляющий собой основное отношение, связывающее выход объекта при заданном начальном состоянии с входными воздействиями:

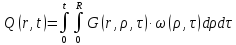(1.14)

В данном случае примем радиус диска R=10 м. Вычислим интеграл, связывающий выход объекта при заданном начальном состоянии с выходными воздействиями:

Выходная величина Q(r,t) находится как сумма двух составляющих:

Q(r,t)=Q₁(r,t) + Q₂(r,t), (1.15)

где Q₁(r,t) и Q₂(r,t) – первая и вторая составляющие выходной величины и находятся как:

Q₁(r,t)=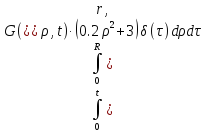 (1.16)

Q₂(r,t)=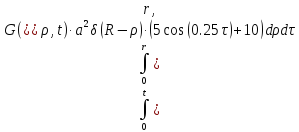 (1.17)

В данных выражениях можно избавиться от одного интеграла, применив свойства δ-функции.

Q₁(r,t)=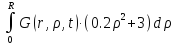 (1.18)

Q₂(r,t)=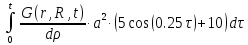 (1.19)

По условию функция Грина имеет вид:

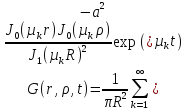(1.20)

Найдем µ_к с помощью пакета прикладных программ MathCad

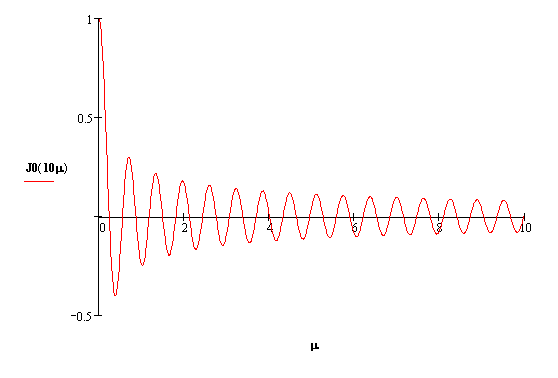
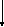
Рисунок 3 – График функции Бесселя

µ_к1=0.24,

µ_к2=0.55,

µ_к3=0.86,

µ_к4=1.17,

µ_к5=1.49.

Первая составляющая решения выходной функции:

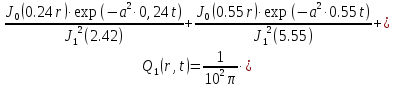
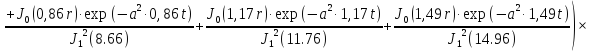
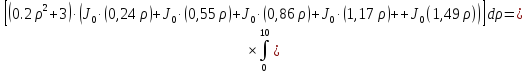
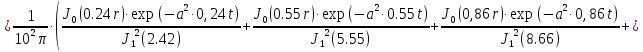
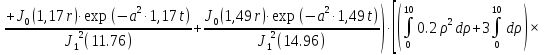
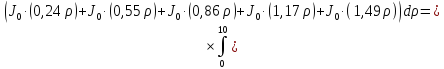
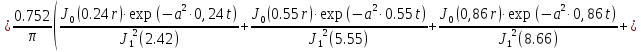
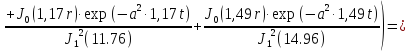
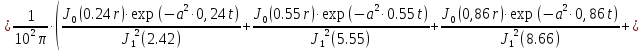
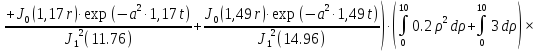
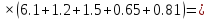
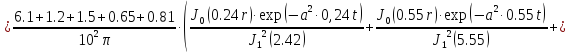
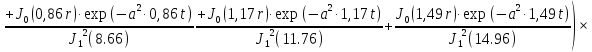
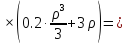
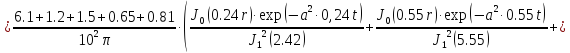
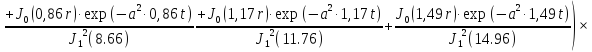
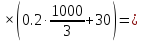
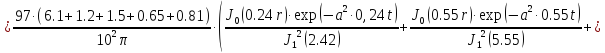
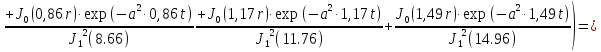
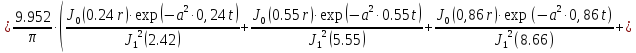
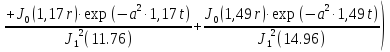(1.21)

Вторая составляющая решения выходной функции:

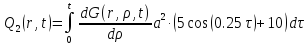(1.22)

Определим производную функции Грина

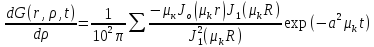(1.23)

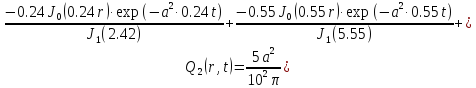
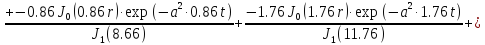
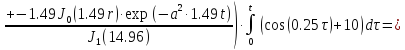
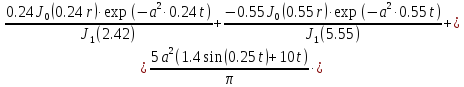
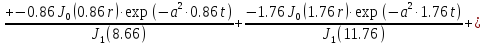
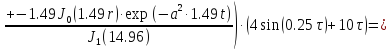
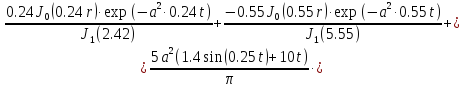
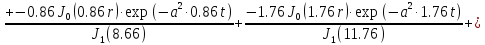
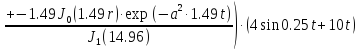(1.24)

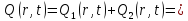
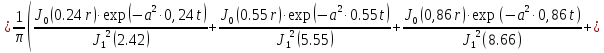
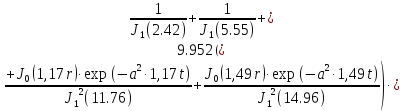
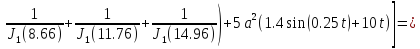
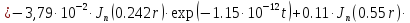
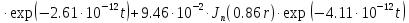(1.25)

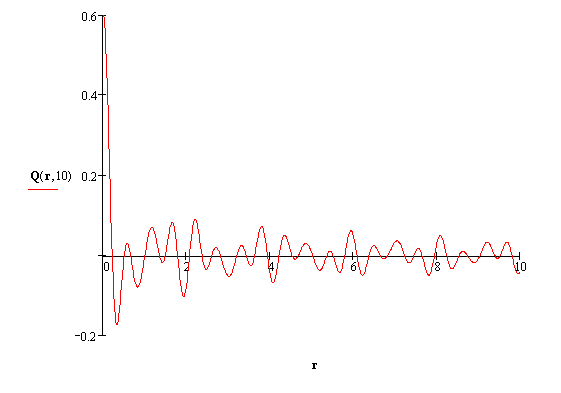
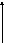
Рисунок 4 – График выходной величины Q(r,t) при t=10 c

1.4 Расчёт динамической характеристики

По заданному дифференциальному уравнению объекта получим выражение для передаточной функции в распределённых параметрах.

Континуальная передаточная функция имеет вид:

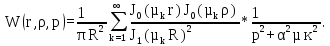(1.26)

Производная по Лапласу от стандартизирующей функции:

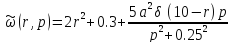(1.27)

Т.к. на систему не действует входное воздействие, то:

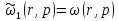(1.28)

Рассчитаем интегральную передаточную функцию как пространственную композицию от произведения континуальной функции W(r,ρ,p) и .

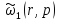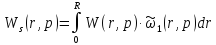(1.29)

Подставим в выражение исходные данные и найдем интегральную передаточную функцию в точке, ограничив количество членов ряда до 3.

При чем

(1.30)

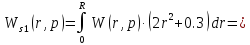
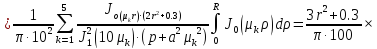
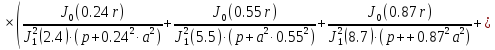
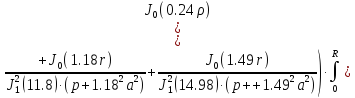
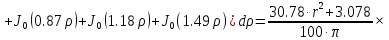
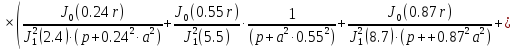
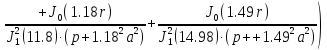(1.31)

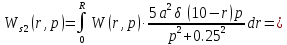
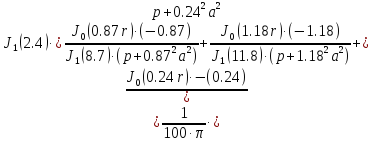
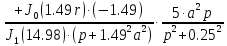(1.32)

Интегральная передаточная функция:

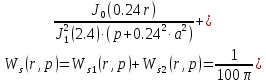
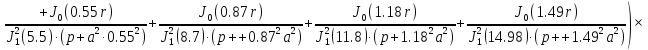
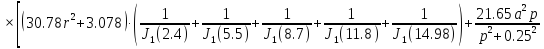(1.33)

Приняв r=R/2=5м и p= iω, получим выражение для частотной передаточной функции:

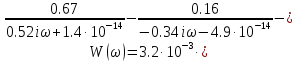
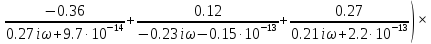
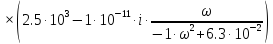(1.34)

1.5 Построение логарифмической амплитудно-частотной характеристики

Построим ЛАЧХ, аппроксимируем, и запишем выражение передаточной функции через типовые звенья.

Построим ЛАЧХ по выражению:

_{20log([Ws(ω)])}

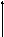
-20 дБ/дек

Рисунок 5 - График логарифмической амплитудно-частотной характеристики

Аппроксимируем полученную ЛАЧХ стандартными типовыми наклонами получаем -20 дБ/дек. Тогда передаточная функция будет иметь вид:

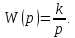(1.35)

График ЛАЧХ пересекает ось y в точке 1 , тогда коэффициент усиления равен:

_{20logk=1, следовательно, k=10.}

С помощью аппроксимации передаточная функция запишется в виде:

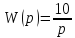. (1.36)

ЗАКЛЮЧЕНИЕ

В ходе выполнения курсовой работы произведено моделирование на микроуровне.

Изучена теория систем с распределенными параметрами применительно к конкретной выбранной задаче математической физики, произведен расчет выходной распределенной величины, интегральной передаточной функции, построены логарифмическая характеристика и ее аппроксимация стандартными типовыми наклонами.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Бутковский А.Г., Характеристики систем с распределенными параметрами. Наука, 1979.-224с.

2. Бессекерский В.А., Попов Н.П. Теория систем автоматического регулирования. М.; Наука 1966.-992с

3. Власов В.В. Синтез интегральной передаточной функции для объектов управления с распределенными параметрами. //Школа академика Власова: Сб. метод, тр-М.,Буркин, 1998.-128с.

Разраб.

Пров.

Изм.

Лист

№ докум.

Подп.

Дата

Н.контр.

Утв.

Лит.

Лист

Листов

2

39

БИТТиУ УИТ-5з

УИТС 423313.208 ПЗ

Моделирование на микро и макро уровне

Пояснительная записка