
курсовая работа / Оптимизация роторно-шарового расходомера Задание №1. Вариант 18
..DOCСАРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ
КАФЕДРА УИТ
КУРСОВАЯ РАБОТА
по курсу: «Моделирование систем управления»
Тема: «Оптимизация роторно-шарового расходомера»
Выполнил: ст. гр. УИТ-42
Принял: преп. кафедры
Фролова М. А.
Балаково 1999.
Задание №1. Вариант 18.
Оптимизация центробежного преобразователя расхода.
Таблица 1
|
Факторы |
Уровни факторов |
|
|
|
-1 |
+1 |
|
Х1 – диаметр входного трубопровода, мм |
0,21 |
0,34 |
|
Х2 – диаметр выходного трубопровода, мм |
0,21 |
0,79 |
|
Х3 – угол криволинейной образующей на входе, |
60 |
360 |
|
Х4 – угол криволинейной образующей на выходе, |
40 |
75 |
Составить 24-1.
X4=X1*X2*X3
Проведем оптимизацию полно факторного эксперимента.
Будем рассматривать задачу с максимальным числом факторов и числом опытов 24-1=8.
Составим матрицу планирования для линейной модели в первом приближении.
Таблица №2
|
|
х0 |
х1 |
х2 |
х3 |
х4 |
Y |
|
S2*10-4 |
y |
у2 |
|
1 |
+ |
- |
- |
- |
- |
1.1 1.12 |
1.11 |
2 |
1.125 |
0.0001 |
|
2 |
+ |
- |
+ |
- |
+ |
2.12 2.143 |
2.132 |
2.645 |
2.168 |
0.000133 |
|
3 |
+ |
+ |
- |
- |
+ |
3.02 3.05 |
3.035 |
4.5 |
3.13 |
0.000225 |
|
4 |
+ |
+ |
+ |
- |
- |
4.61 4.62 |
4.615 |
0.5 |
4.468 |
0.000025 |
|
5 |
+ |
- |
- |
+ |
+ |
5.11 5.14 16 |
5.125 |
4.5 |
4.978 |
0.000225 |
|
6 |
+ |
- |
+ |
+ |
- |
6.21 6.23 |
6.22 |
2 |
6.315 |
0.0001 |
|
7 |
+ |
+ |
- |
+ |
- |
7.25 7.234 |
7.242 |
1.28 |
7.278 |
0.000064 |
|
8 |
+ |
+ |
+ |
+ |
+ |
8.3 8.31 |
8.305 |
0.5 |
8.32 |
0.000025 |
Подсчитываем средние значения в сериях Y.
![]()
где уi – i-тое значение в серии опытов; n – количество серий опытов.
Подсчитываем дисперсию S2 различных серий опытов.
![]()
Проверяем пятую серию опытов на наличие ошибки.
Так как дисперсия S2=0,00045, то
![]() =
512,65 >
t
=
12,71
=
512,65 >
t
=
12,71
где t – коэффициент Стьюдента для степени свободы (n – 1)=(2 – 1)=1.
А значит значение опыта равное 16 – промах и из дальнейшего рассмотрения мы его исключаем.
Проверяем дисперсию на однородность.
S2max / S2min = 0.00045 / 0.00005 = 9
Полученное значение меньше табличного значения критерия Фишера равного F=164,4 для степеней свободы числителя f2 = n - 1=1 и знаменателя
f1 = n – 1=1, значит дисперсии однородны.
Находим дисперсию выходного параметра.
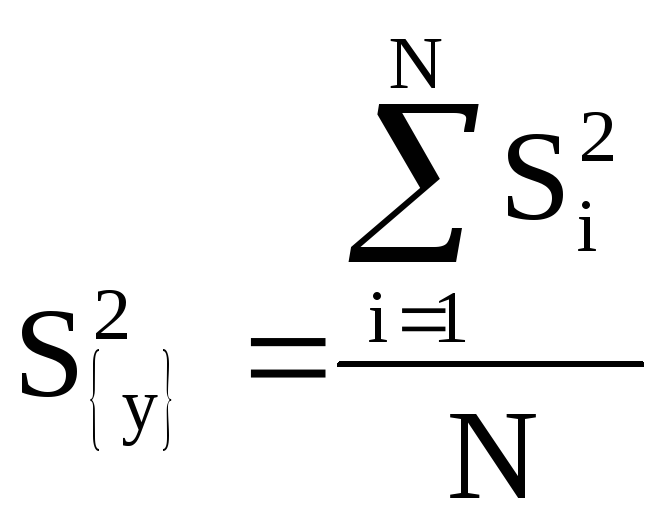 =
0,0002241
=
0,0002241
Записываем линейную модель в первом приближении в виде:
у=b0 + b1х1 + b2х2 + b3х3 + b4x4
пренебрегая влиянием составляющих второго порядка.
bi=![]()
Получили следующие коэффициенты:
b0 = 4.723 ;
b1 = 1.076 ;
b2 = 0.595 ;
b3 = 2 ;
b4 = -0.074 ;
Линейная модель запишется в виде:
у = 4.723 + 1.076х1 + 0.595х2 + 2х3 - 0.074x4
Рассчитываем по этой модели расчетные значения параметра оптимизации y = f(x) и заносим эти значения в таблицу.
После чего находим квадрат отклонения расчетного значения от экспериментального
у2 = ( y - )2
и заносим полученные значения в таблицу.
Затем находим дисперсию адекватности для равномерного дублирования
S2ад
=
![]() =
0.043
=
0.043
где f2 = N - (k + 1) = 8 – (4+1) = 3, n = 2.
Проверяем модель на адекватность, для чего находим расчетный коэффициент Фишера как отношение:
Fрасч=S2ад/S2y=0.043/0.0002241=191.87
Полученное значение сравниваем с табличным значением критерия Фишера F = и поскольку полученное значение больше его, то полученная линейная модель адекватна.
Оценим значимость коэффициентов, для чего найдем дисперсию коэффициентов регрессии:
![]() =
0.0002241/8 =
0,00002801
=
0.0002241/8 =
0,00002801
Определим доверительный интервал
bj = ± t S{b} = 12,71 · 0,00002801 = 0,000356
Так как все коэффициенты по абсолютной величине больше доверительного интервала, то все они значимы.
Приступим к нахождению максимального значения параметра оптимизации движением по градиенту.
Таблица №3
|
Натур. Значения |
Х1 |
Х2 |
Х3 |
Х4 |
|
У |
|
Основной ур. |
0.275 |
0.5 |
210 |
57.5 |
|
|
|
Верхний ур. |
0.34 |
0.79 |
360 |
75 |
|
|
|
Нижний ур. |
0.21 |
0.21 |
60 |
40 |
|
|
|
J |
0.65 |
0.29 |
150 |
17.5 |
|
|
|
Кодир. значения |
|
|
|
|
|
|
|
1 |
- |
- |
- |
- |
|
1.11 |
|
2 |
- |
+ |
- |
+ |
|
2.132 |
|
3 |
+ |
- |
- |
+ |
|
3.035 |
|
4 |
+ |
+ |
- |
- |
|
4.615 |
|
5 |
- |
- |
+ |
+ |
|
5.125 |
|
6 |
- |
+ |
+ |
- |
|
6.22 |
|
7 |
+ |
- |
+ |
- |
|
7.242 |
|
8 |
+ |
+ |
+ |
+ |
|
8.305 |
|
.bj |
1.076 |
0.595 |
2 |
-0.074 |
|
|
|
.bjJj |
0.07 |
0.173 |
300.009 |
-1.292 |
|
|
Уменьшим bjJj в десять раз.
Таблица №4
|
Шаг |
0,007 |
0,0173 |
30,0009 |
-0,1292 |
|
Мысленные опыты |
|
|
|
|
|
1 |
0,282 |
0,517 |
240 |
57,371 |
|
2 |
0,289 |
0,535 |
270 |
57,242 |
|
3 |
0,296 |
0,552 |
300 |
57,212 |
|
4 |
0,303 |
0,569 |
330 |
56,983 |
|
5 |
0,31 |
0,586 |
360 |
56,854 |
|
|
|
|||
Вычислим значения параметров оптимизации по линейной модели.
![]()
. Таблица №5
|
№ |
X1 |
X2 |
X3 |
X4 |
|
.y |
|
1 |
0.108 |
0.059 |
0.2 |
-0.007381 |
|
5.275 |
|
2 |
0.215 |
0.119 |
0.4 |
-0.015 |
|
5.827 |
|
3 |
0.323 |
0.178 |
0.6 |
-0.022 |
|
6.378 |
|
4 |
0.431 |
0.238 |
0.8 |
-0.03 |
|
6.93 |
|
5 |
0.538 |
0.297 |
1 |
-0.037 |
|
7.482 |
|
|
|
|
|
|||
Сравнивая, экспериментальные значения параметра оптимизации и полученные при реализации мысленных опытов нашли, что максимальное значение параметра оптимизации равно у = 8.305, оно получено при значении факторов X1 = 0.34, X2 = 0.79, X3 = 360, X4 = 75.
