
- •2.1 Графические формы математической модели гидравлической системы 16
- •2.2 Матричные формы математической модели гидравлической
- •Приложение а 35
- •0 ДБ/дек -40 дБ/дек -20 дБ/дек
- •2.1 Графические формы математической модели гидравлической системы
- •2.2 Матричные формы математической модели гидравлической системы
2.2 Матричные формы математической модели гидравлической системы
На основании орграфа (рисунок 11) сформируем матрицу инциденций (таблица 1), по правилам, изложенным в основных теоретических сведениях.
Для формирования полной математической модели на основе компонентных и топологических уравнений широкое применение получил узловой метод, для него необходимо сформировать матрицу инциденций, отражающую структуру связей всех элементов системы. Матрица инциденций формируется на основании ориентированного графа. Число строк матрицы соответствует числу узлов орграфа, число столбцов – числу ветвей. Отсутствие связи между узлом и ветвью обозначается «0», если ветвь входит в узел – «1», если выходит – «–1».
Матрицу инциденций А можно представить состоящей из подматриц инерционных АИ, диссипативных АД, упругих АУ ветвей и подматрицы ветвей источников потенциалов АВ. Для исходной системы получена матрица, представленная в таблице 1.
Таблица 1 – Матрица инциденций гидравлической системы
|
Узлы |
Ветви | ||||||||||
|
Диссипативные |
Упругие |
Внешние воздействия | |||||||||
|
μ1 |
μ2 |
μ3 |
μ4 |
μ5 |
с1 |
рВ1 |
рВ2 |
рВ3 |
рВ4 |
pн | |
|
1 |
-1 |
0 |
0 |
0 |
0 |
1 |
-1 |
0 |
0 |
0 |
0 |
|
2 |
0 |
-1 |
0 |
0 |
0 |
1 |
0 |
-1 |
0 |
0 |
0 |
|
3 |
0 |
0 |
-1 |
0 |
0 |
1 |
0 |
0 |
-1 |
0 |
0 |
|
4 |
0 |
0 |
0 |
-1 |
0 |
1 |
0 |
0 |
0 |
-1 |
0 |
|
5 |
0 |
0 |
0 |
0 |
-1 |
-1 |
0 |
0 |
0 |
0 |
1 |
|
подматрицы |
АД |
АУ |
АВ | ||||||||
На основании матрицы инциденций записывают подматрицы упругих АУ, диссипативных АД элементов и подматрицу источников потенциалов АВ.
 ,
,
 ,
,
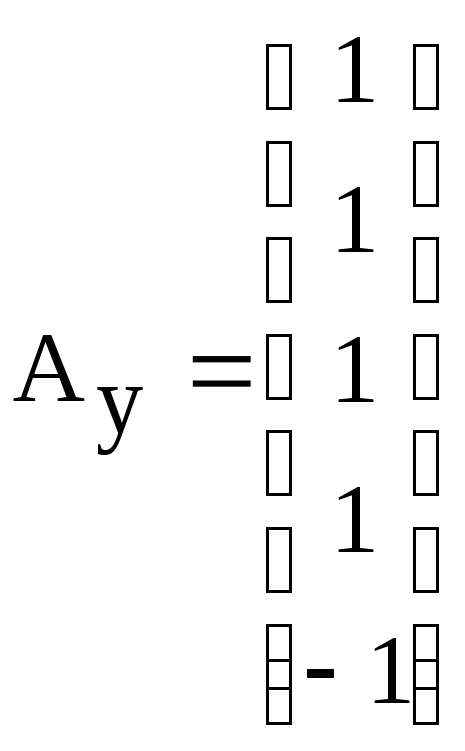 .
.
Матрицы параметров инерционных, упругих и диссипативных элементов гидравлической системы соответственно.
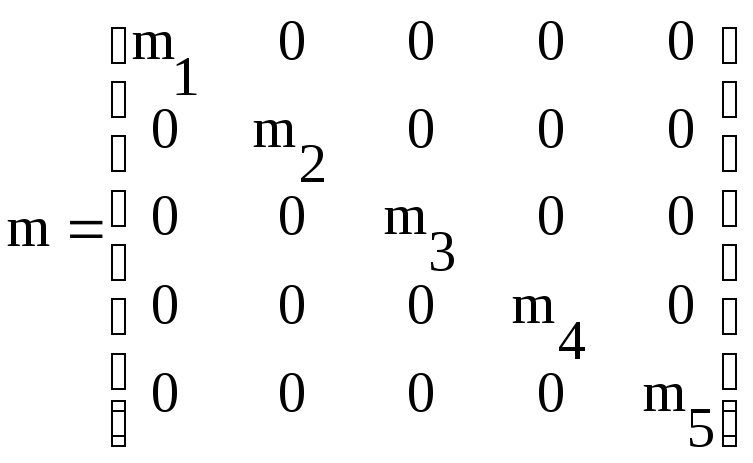 ,
,
![]() ,
, .
.
Матрица потенциалов источников Рв, упругих Ру и диссипативных Рд, элементов и матрица фазовых переменных типа потока Q.
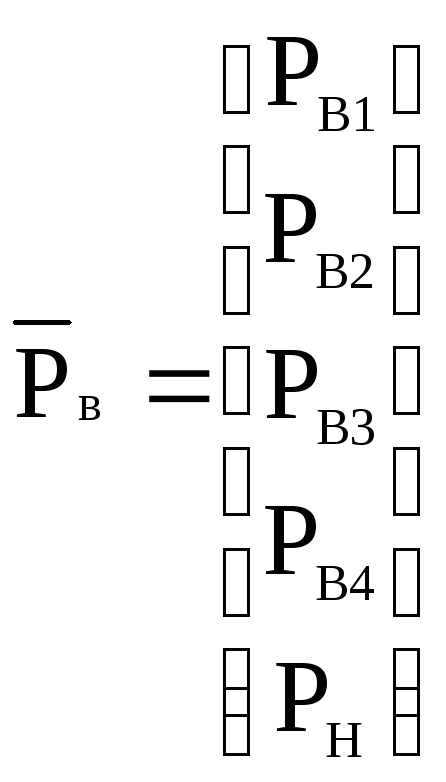 ,
,
![]() ,
,
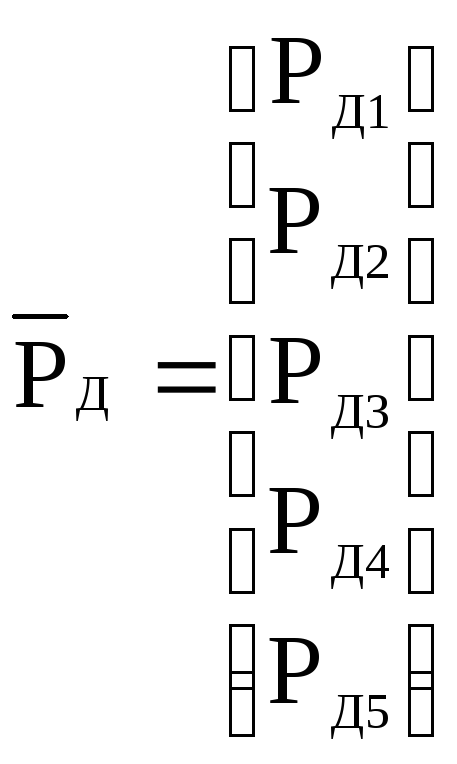 ,
,
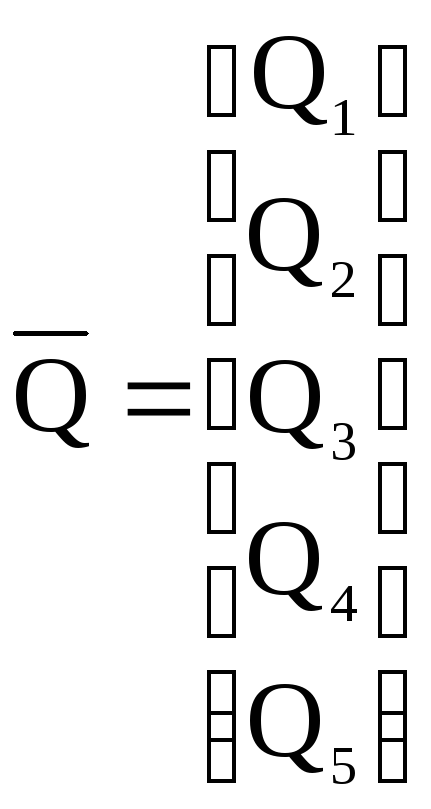 .
.
2.3 Узловой метод формирования математической модели гидравлической
системы
Из матрицы инциденций можно получить систему уравнений (15), математически описывающую функционирование гидравлической системы:
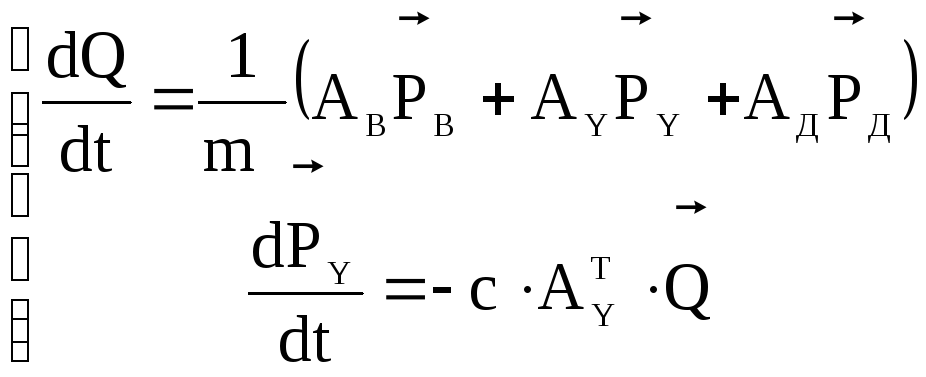 (15)
(15)
где
![]() .
.
Для нашего случая система будет иметь вид:
(16)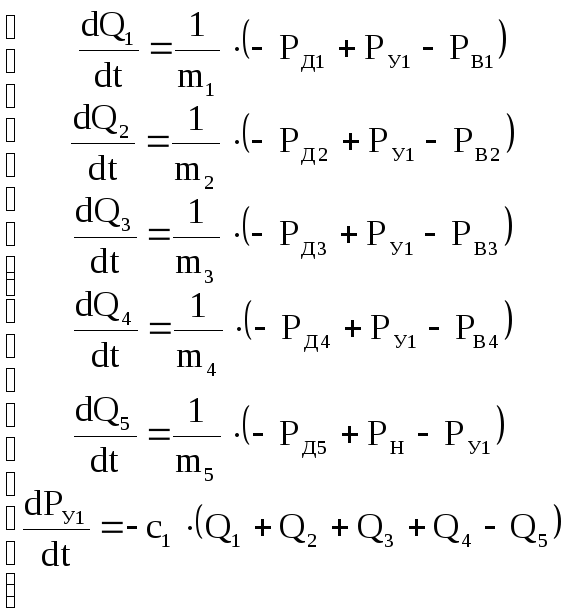
Комплексные уравнения диссипативных элементов носят более сложный характер, при этом выделяют линейные и нелинейные потери давления в гидромагистралях, их уравнения запишутся в следующем виде:
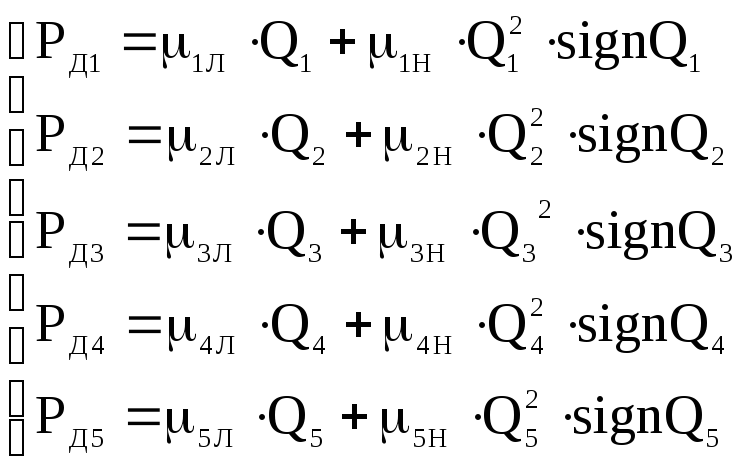 (17)
(17)
где
![]() коэффициент
гидравлического сопротивления,
характеризующий
коэффициент
гидравлического сопротивления,
характеризующий
линейные потери при ламинарном режиме движения жидкости;
![]() коэффициент
гидравлического сопротивления,
характеризующий
коэффициент
гидравлического сопротивления,
характеризующий
нелинейные потери при турбулентном режиме, по длине и местные.
Таким образом, математическая модель рассматриваемой гидросистемы представляется системой шести дифференциальных уравнений.
2.4 Расчет параметров элементов гидросистемы
Исходные данные представлены в таблице 2.
Таблица 2 – Параметры системы и жидкости
-
Обозначение
Основные параметры
Значение

Плотность рабочей жидкости
860 кг/м3

Вязкость
0.15·10-4 м2/с
ЕС
Модуль упругости системы
1.7·108 Па
Етр
Модуль упругости трубопровода
2.1·1011 Па
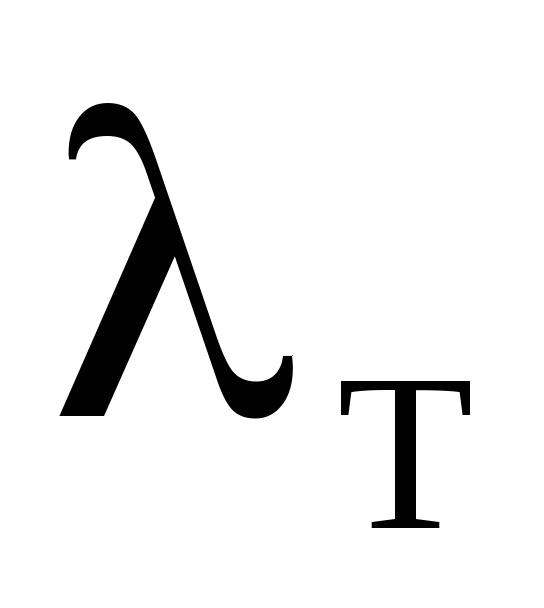
Коэффициент потерь на трение при турбулентном потоке
0.03

Толщина стенки трубопровода
2.2·10-3 м
Таблица 3 – Параметры трубопроводов
|
Параметр |
Обозначение |
Номер трубопровода | ||||
|
1 |
2 |
3 |
4 |
5 | ||
|
Диаметр трубопровода |
dтр, м |
0.01 |
0.015 |
0.015 |
0.01 |
0.02 |
|
Длина трубопровода |
l, м |
1.8 |
2 |
2 |
1.5 |
0.6 |
|
Коэффициент местных сопротивлений |
ξ |
4.5 |
5 |
4.5 |
4 |
3 |
|
Давление потребителей и насосов |
P, ·106 Па |
0.1 |
0.19 |
0.19 |
0.16 |
0.2, 0.4 |
На основании исходных данных рассчитаем параметры компонентных элементов для каждого участка трубопровода по формулам:
– площадь сечения трубопровода, м2:
![]() ;
(18)
;
(18)
– коэффициент линейных потерь, H·с/м5:
![]() ;
(19)
;
(19)
– коэффициент нелинейных потерь, H·с/м5:
![]() ;
(20)
;
(20)
– коэффициент жесткости участка, H/м5:
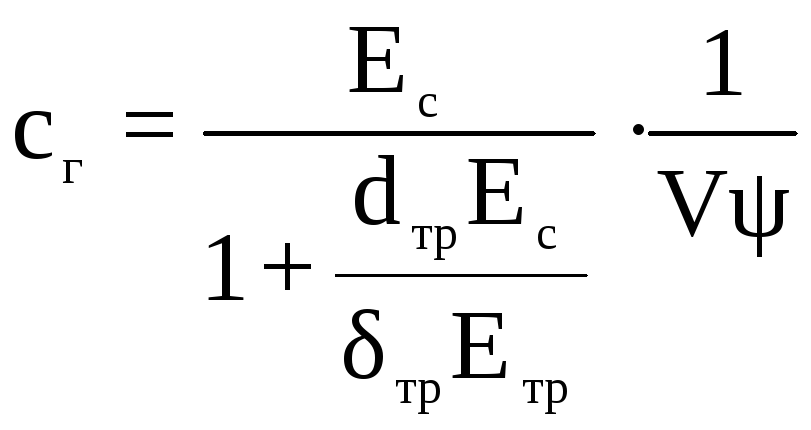 ;
(21)
;
(21)
где Ψ – доля объема трубопровода;
V – объем трубопровода, м3:
![]() (22)
(22)
Доля объема трубопровода рассчитывается как отношение объема отдельного участка к сумме объемов всех n соединенных между собой участков:
![]() (23)
(23)
Коэффициент жесткости упругого элемента:
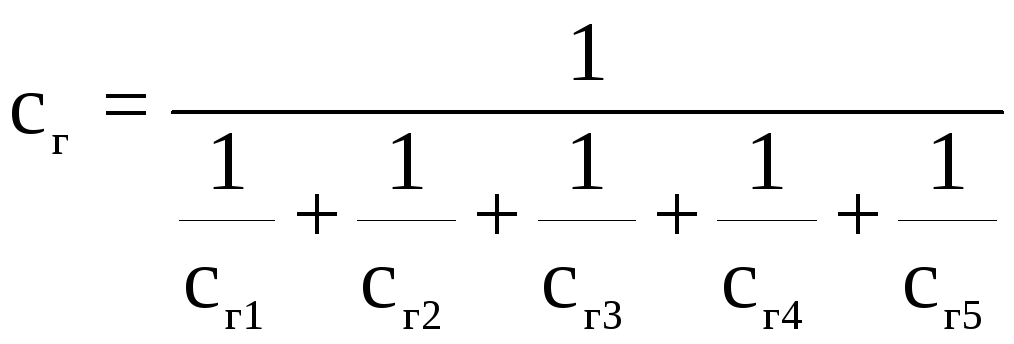 (24)
(24)
По исходным данным и полученным результатам получаем жесткость упругого элемента c1= 0,612·1012 Н/м5.
Коэффициент массы, кг/м4:
![]() .
(25)
.
(25)
Полученные результаты для отдельных участков трубопровода приведены в таблице 4.
Таблица 4 – Параметры трубопровода гидросистемы
|
Параметр |
Номер магистрали | ||||
|
1 |
2 |
3 |
4 |
5 | |
|
Площадь сечения трубопровода, A, ·10-4 м2 |
0.785 |
1.766 |
1.766 |
0.785 |
3.14 |
|
Объем трубопровода, Vтр,·10-4 м3 |
1.413 |
3.532 |
3.532 |
1.1775 |
1.884 |
|
Доля
объема трубопровода,
|
0.122 |
0.306 |
0.306 |
0.102 |
0.163 |
|
Коэффициент массы, mг,·106 кг/м4 |
19.72 |
9.74 |
9.74 |
16.43 |
1.64 |
|
Коэффициент
линейных потерь, |
9.5 |
2.085 |
2.085 |
7.91 |
0.2 |
|
Коэффициент
нелинейных потерь, |
69.1 |
12.4 |
11.7 |
59.3 |
1.7 |
|
Коэффициент жесткости участка, cг, ·1012 Н/м5 |
9.825 |
1.564 |
1.564 |
14.102 |
5.495 |
2.5 Расчет статического режима работы гидросистемы
При постоянных внешних воздействиях система находится в установившемся равновесном состоянии, а её фазовые координаты при этом постоянны. Такой режим функционирования системы называется статическим и достигается при постоянных внешних воздействиях: подачей насоса Pн; давлениями потребителей Рв1,Рв2, Рв3, Рв4.
При этом фазовыми (искомыми) координатами системы являются: расходы в гидромагистралях Q1, Q2, Q3, Q4, Q5; давление в упругом элементе Ру1.
Модель гидросистемы в статическом режиме имеет вид:
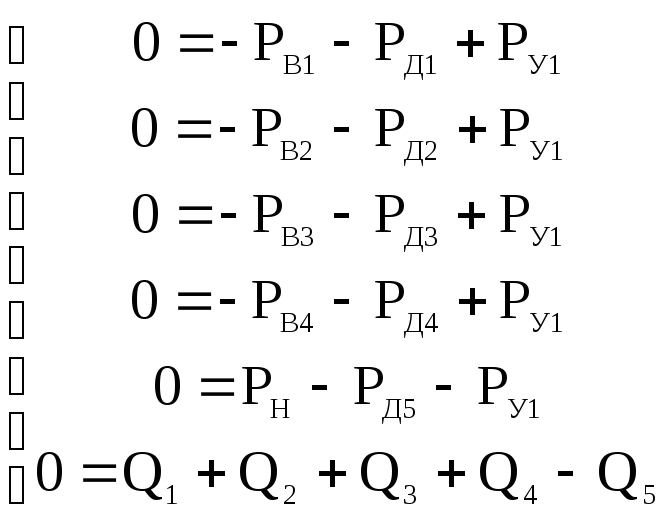 (26)
(26)
Систему (26) будем решать с помощью численного метода Ньютона. Предварительно сформируем матрицу Якоби, элементами которой являются частные производные, уравнения статической модели по фазовым координатам. В общем виде матрица Якоби имеет вид:
 (27)
(27)
Для диссипативных элементов компонентное уравнение имеет вид:
(28)![]()
Ч
(29)![]()
Матрица Якоби исходной гидросистемы имеет вид:
(30)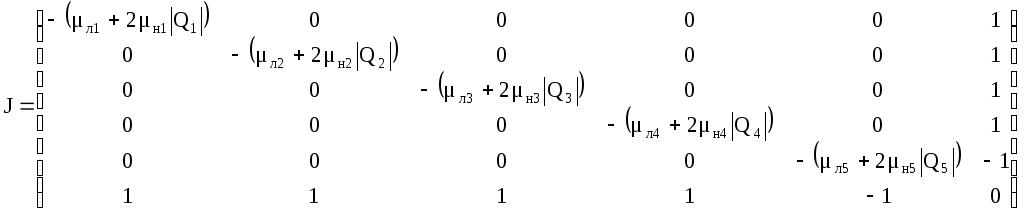
Алгоритм метода Ньютона содержит следующие этапы:
1)
выбор начального приближения
![]() ,
где
,
где![]() – вектор фазовых координат,V0
– нулевой вектор-столбец;
– вектор фазовых координат,V0
– нулевой вектор-столбец;
2)
вычисление матрицы Якоби Jk
в точке
![]() K,
где k
= 0, 1, 2 … – номер итерации;
K,
где k
= 0, 1, 2 … – номер итерации;
3)
вычисление вектора невязок
![]() :
:
4) определение вектора поправок:
![]() ;
(32)
;
(32)
5) определение нового приближения вектора искомых фазовых координат:
![]() ;
(33)
;
(33)
6)
проверка условия окончания итерационного
процесса при выполнении условия, что
![]() и
и
![]() соизмеримы (совпадают до десятых), иначе
происходит переход на предыдущие этапы
и вычисляется следующая итерация.
соизмеримы (совпадают до десятых), иначе
происходит переход на предыдущие этапы
и вычисляется следующая итерация.
Расчет фазовых координат в статическом режиме осуществлен MathCad, а результаты представлены в таблице 5.
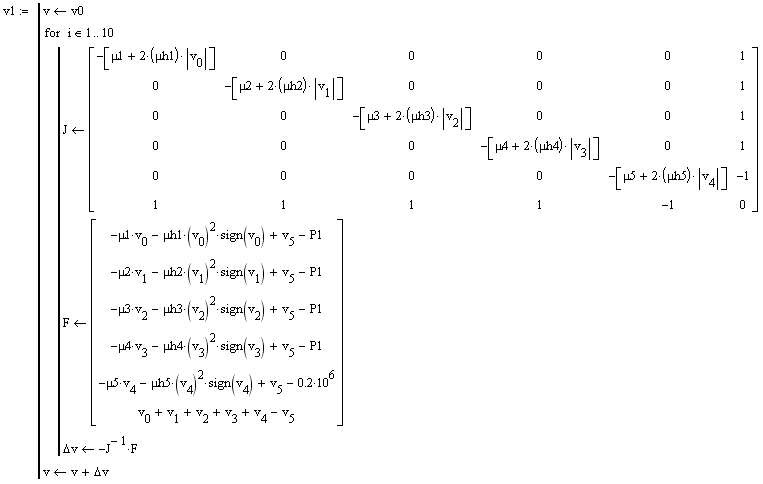
Таблица 5 – Результаты статического анализа
|
Фазовые координаты |
Pн=0.2∙106 Па |
Pн=0.4∙106 Па |
|
Q1, м3/c |
2.55∙10-3 |
4.251∙10-3 |
|
Q2, м3/c |
0.012 |
0.019 |
|
Q3, м3/c |
0.012 |
0.019 |
|
Q4, м3/c |
3.063∙10-3 |
5.105∙10-3 |
|
Q5, м3/c |
0.029 |
0.048 |
|
Ру1, Па |
1.423∙105 |
3.038∙105 |
2.6 Анализ динамических свойств гидросистемы
Динамическая модель описывает переходный процесс гидросистемы. В общем случае система дифференциальных уравнений, описывающих гидравлическую систему, имеет вид:
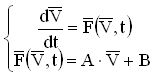 (34)
(34)
С учетом произведенных ранее расчетов, запишем систему дифференциальных уравнений (35), представляющую собой динамическую модель гидросистемы:
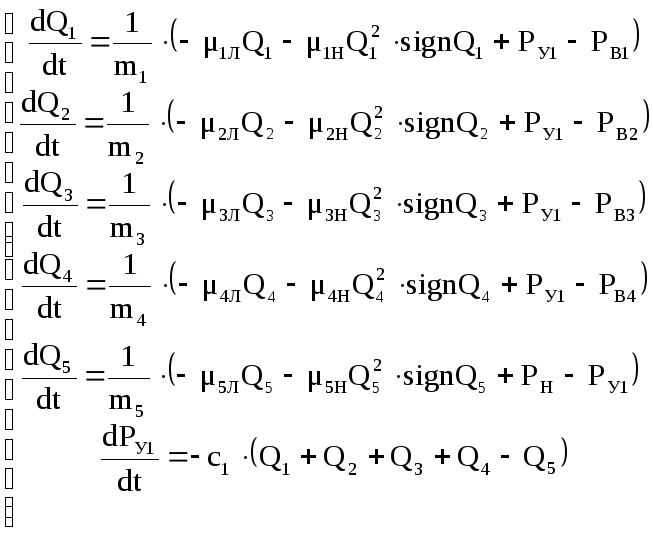 (35)
(35)
Для динамической модели матрица Якоби формируется аналогично матрице Якоби статической модели:
(36)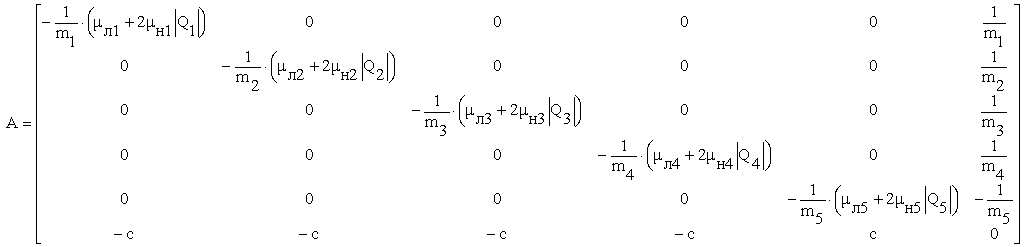
Переходный процесс определяется в результате численного интегрирования системы (35), для чего необходимо произвести выбор ряда параметров.
Переходный процесс оценивается как реакция системы, находящейся в состоянии покоя, на ступенчатое воздействие вида:
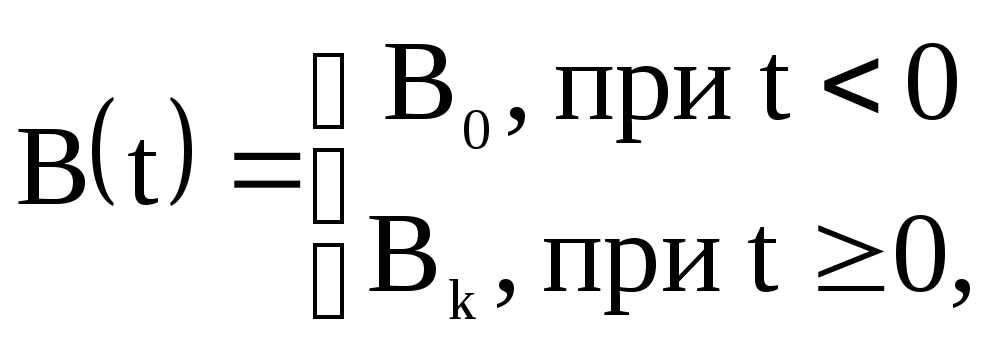 (37)
(37)
где В0 и Вk – начальное и конечное значения функции внешних воздействий В(t),
причем В 0 и В k – const, (В 0 ≠ В k):
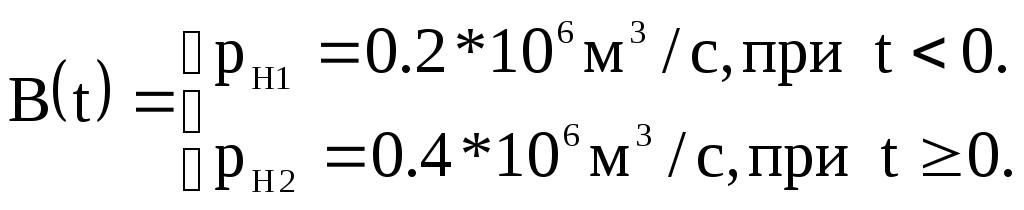 (38)
(38)
Начальные и конечные значения вектора фазовых координат определены при анализе статического режима (таблица 5).
 =>
=>
 (39)
(39)
Если
система устойчивая, то через некоторый
промежуток времени, система перейдет
из состояния
![]() в состояние
в состояние
![]() .
Вектор-функция внешних воздействий В
имеет вид:
.
Вектор-функция внешних воздействий В
имеет вид:
(40)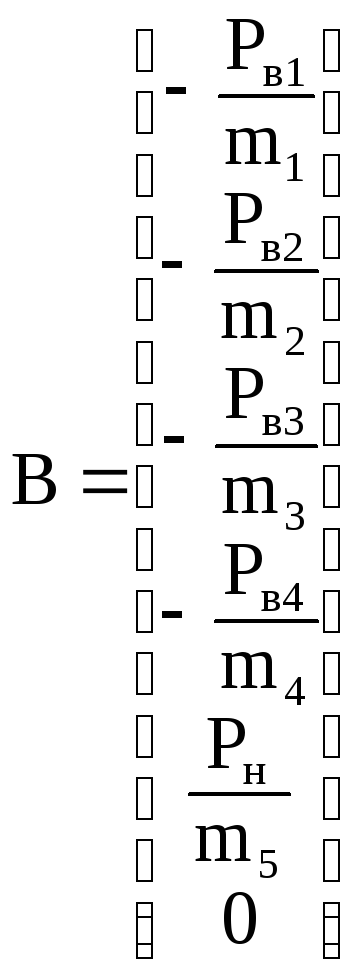
Для устойчивости самого метода проведем выбор шага интегрирования h исходя из условия:
![]() ,
(41)
,
(41)
где
![]() – собственное значение матрицы Якоби.
– собственное значение матрицы Якоби.
Для
комплексного значения
![]() условие имеет вид:
условие имеет вид:
![]() .
(42)
.
(42)
Собственными
значениями матрицы Якоби порядка n
называют корни
![]() ,
где
,
где![]() ,
ее характеристического уравнения,
определяемого по формуле:
,
ее характеристического уравнения,
определяемого по формуле:
![]() (43)
(43)
Произведем расчет матрицы Якоби по формуле (36), подставляя начальные значения фазовых координат:
(44)

Тогда характеристическое уравнение имеет вид:
![]() (45)
(45)
Вычислим корни характеристического уравнения с помощью программы MathCad, тогда собственные значения матрицы Якоби имеют вид:
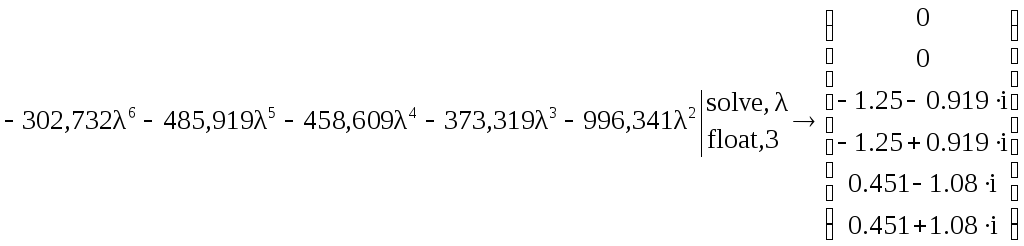 (46)
(46)
Корни характеристического уравнения имеют и отрицательные, и положительные значения действительных частей, что говорит о неустойчивости системы.
Наличие комплексно-сопряженных корней дает затухающий колебательный процесс ряда фазовых координат. Для гидравлической системы рекомендуемый шаг интегрирования h=0.5с. Выполним проверку устойчивости численного метода Эйлера при данном шаге.
При λ = 0: |1h·λ| = 1.
При λ = 1,25 0,919·i:
(Re(h·λ)12 + Im(h·λ)2 = 2.852.
При λ = 1,25 0,919·i:
(Re(h·λ)12 + Im(h·λ)2 = 2.429.
При λ = 1.08·i:
(Re(h·λ)12 + Im(h·λ)2 = 0.891.
При λ = 1.08·i:
(Re(h·λ)12 + Im(h·λ)2 = 0.308.
Проверка условий выполняется, следовательно, шаг h=0.5 обеспечит устойчивость метода и приемлемую точность вычислений.
Для численного интегрирования исходной системы дифференциальных уравнений будем использовать неявный метод Эйлера, формула которого имеет вид:
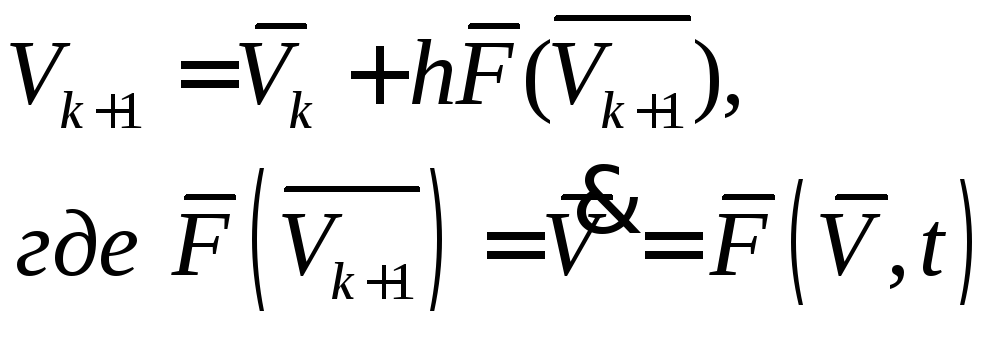 (47)
(47)
Совместное преобразование двух последних выражений приводит к виду:
![]() ,
(48)
,
(48)
где
![]()
модифицированная матрица Якоби на
(k+1)ом
шаге, которая
модифицированная матрица Якоби на
(k+1)ом
шаге, которая
формируется по следующему правилу:
а) диагональные элементы матрицы Якоби на (k+1)ом шаге
пересчитываются по формуле:
![]() ,
(49)
,
(49)
где h – шаг интегрирования.
б) остальные элементы не изменяются:
![]() .
.
![]() –модифицированный
вектор входных воздействий на (k+1)ом
шаге,
–модифицированный
вектор входных воздействий на (k+1)ом
шаге,
определяемый по формуле:
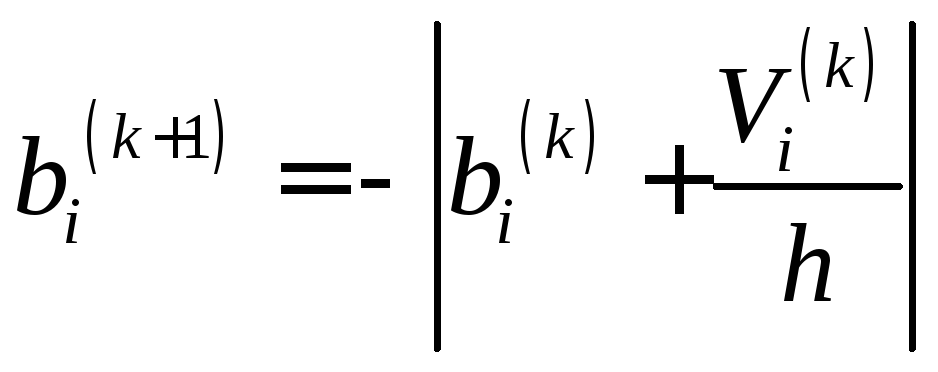 (50)
(50)
Решение системы уравнений (47) дает значение вектора фазовых координат на (k+1)ом шаге, то есть в момент времени tk+1.
Алгоритм неявного метода Эйлера с постоянным шагом интегрирования h:
задание шага интегрирования: h = 0,5;
задание начальных значений вектора фазовых переменных
 приt0=0;
приt0=0;вычисление времени tk+1=tk+h, где k = 0, 1, 2…;
вычисление модифицированных матриц
 и
и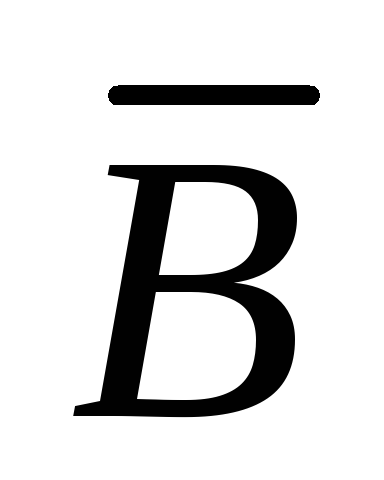 на (k+1)ом
шаге;
на (k+1)ом
шаге;решение системы уравнений (61) с целью определения
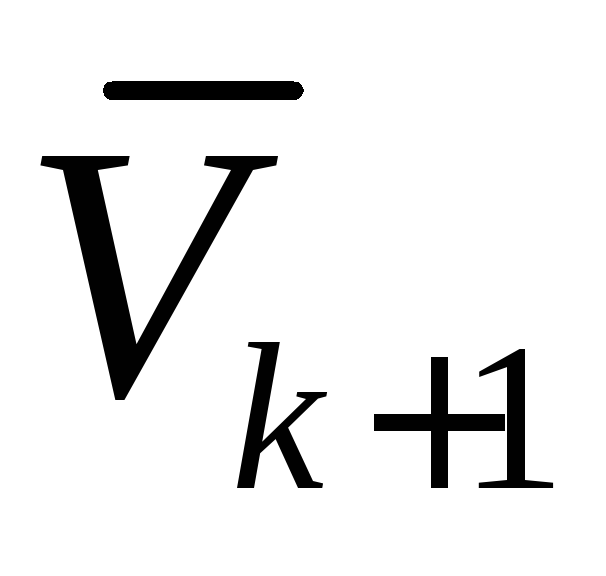 в
момент
в
момент
времени tk+1;
переход к этапу (3) до тех пор, пока в случае устойчивой системы
фазовые
координаты не достигнут состояния
конечного значения
![]() .
.
Начальные
значения вектора
![]() определяются на основании входных
воздействий системы. В качестве начальных
значений фазовых переменных берем
вектор начальных значений
определяются на основании входных
воздействий системы. В качестве начальных
значений фазовых переменных берем
вектор начальных значений![]() .
.
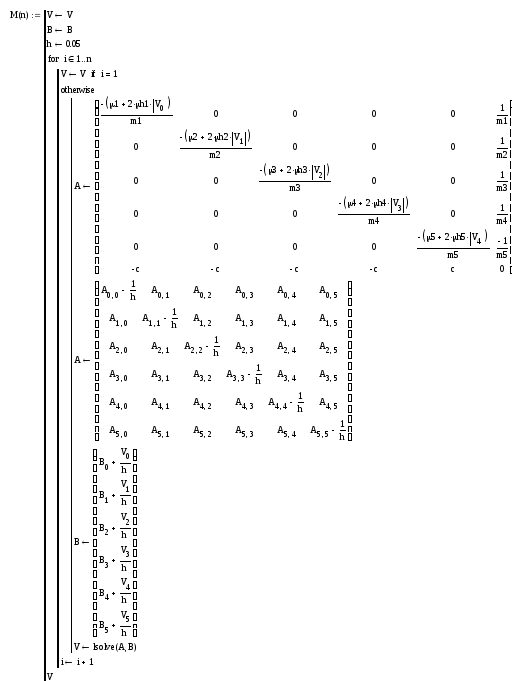
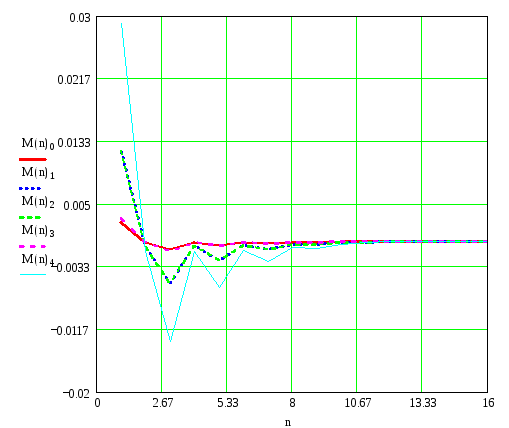


Рисунок 12 – Графики переходных процессов расходов Q1, Q2, Q3, Q4, Q5
Вывод: из графика на рисунке 12 видно, что переходные процессы расходов Q1, Q2, Q3, Q4, Q5 имеют затухающий вид и достигают установившегося состояния при n=10,5.
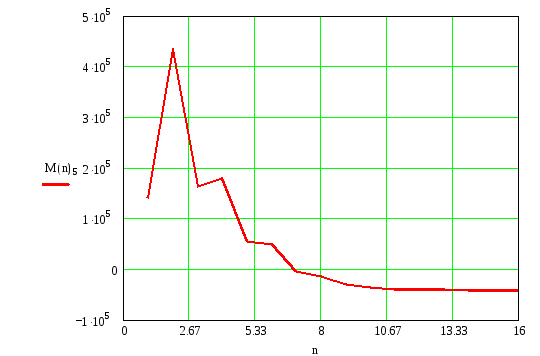


Рисунок 13 – Переходный процесс давления упругого элемента РУ1
Вывод: из графика на рисунке 13 видно, что переходный процесс давления упругого элемента Py1 имеет затухающий вид и достигает установившегося состояния при n=10,6, что говорит об устойчивости гидросистемы.
ЗАКЛЮЧЕНИЕ
В ходе выполнения курсовой работы произведено моделирование на микро- и макроуровнях.
В первой части работы произведена идентификация заданного дифференциального уравнения, по полученному уравнению гиперболического типа построен график изменения внешнего воздействия (давления, нормированного плотностью материала струны), представляющий собой гармонические колебания, а также график выходной распределенной величины при фиксированном времени t = 8 c.
Синтезирована
интегральная передаточная функция, в
результате чего получена передаточная
функция
![]() ,
на основании которой построена ЛАЧХ.
После проведения аппроксимации полученной
ЛАЧХ типовыми наклонами, найдено
уравнение передаточной функцииWап.(p).
,
на основании которой построена ЛАЧХ.
После проведения аппроксимации полученной
ЛАЧХ типовыми наклонами, найдено
уравнение передаточной функцииWап.(p).
При условии, что струна жестко закреплена по длине, смоделировано колебание струны в программе Elcut, решение задачи получено в виде цветовой шкалы.
Во второй части работы по схеме гидравлической системы найдены основные параметры трубопровода, произведен расчет статической и динамической модели. Система дифференциальных уравнений статической модели решена методом Ньютона, а динамическая модель рассчитана методом Эйлера. Построены переходные процессы расходов и давлений упругих элементов гидросистемы.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
Бутковский А.Г. Характеристики систем с распределенными параметрами/А.Г. Бутковский. – М.: Наука, 1979. – 224 с.
Бесекерский В.А. Теория систем автоматического регулирования /В.А. Бесекерский, Е.П. Попов. – М.: Профессия, 2003. – 380 с.
Власов В.В. Синтез интегральной передаточной функции для объектов управления с распределенными параметрами // Школа академика Власова: Сб. метод, тр – М.: Буркин, 1998. – 128 с.
Топчеев Ю.И. Атлас для проектирования систем автоматического управления. – М.: Машиностроение, 1982. – 312 с.
Цыпкин Я. 3. Основы теории автоматических систем. М.: Наука, 1977. – 560 с.
Чемоданов Б.К. Математические основы теории автоматического регулирования/Б.К. Чемоданов и [др.]. – М.: Высшая школа, 1977. – 366 с.
ПРИЛОЖЕНИЕ А
(обязательное)
Графическая часть
1 Моделирование на микроуровне. Идентификация краевой задачи 36
2 Расчет выходной распределенной величины 37
3 Расчет динамической характеристики 38
4 Моделирование на макроуровне. Исходные данные 39
5 Графические и табличные формы гидравлической модели 40
6 Расчет статического режима работы гидросистемы 41
7 Расчет динамического режима работы гидросистемы 42
