-37

СОДЕРЖАНИЕ

Введение 3

1 Моделирование на микроуровне 5

1.1 Исходные данные 5

1.2 Идентификация краевой задачи 5

1.3 Расчет выходной распределенной величины 9

1.4 Расчет интегральной передаточной функции 11

1.5 Моделирование струны в среде Elcut 14

2 Моделирование на макроуровне 16

2.1 Графические формы математической модели гидравлической системы 16

2.2 Матричные формы математической модели гидравлической

системы 18

2.3 Узловой метод формирования математической модели

гидравлической системы 20

2.4 Расчет параметров элементов гидросистемы 21

2.5 Расчет статического режима работы гидросистемы 24

2.6 Анализ динамических свойств гидросистемы 26

Заключение 33

Список использованных источников 34

Приложение а 35

ВВЕДЕНИЕ

Под моделью понимают такой материальный или мысленно представляемый объект, который в процессе изучения замещает объект – оригинал, сохраняя некоторые возможные для данного исследования типичные его черты.

Процесс построения и использования модели называется моделированием.

Различают моделирование предметное и абстрактное.

При предметном моделировании строят физическую модель, которая соответствующим образом отображает физические свойства объекта, при этом объект может иметь иную физическую природу. Недостаток такого вида моделирован – большие временные и материальные затраты.

Абстрактное моделирование связано с построением абстрактной модели (математические соотношения, графы, схемы, диаграммы). Наиболее мощным средством абстрактного моделирования является математическое моделирование.

Математическое моделирование позволяет посредством математических символов и зависимостей составить описание функционирования технического объекта в окружающей внешней среде, определить выходные параметры и характеристики, получить оценку показателей эффективности и качества, осуществить поиск оптимальной структуры и параметров объекта.

Математическая модель – совокупность математических объектов и отношений между ними, адекватно отображающих физические свойства объекта.

В зависимости от степени абстрагирования различают три основных иерархических уровня: верхний (меттауровень), средний (макроуровень), нижний (микроуровень).

Микроуровень – это нижний иерархический уровень, где композиция объектов по степени абстрагирования. На этом уровне осуществляется детальное описание физических свойств технического объекта. Объекты рассматриваются как сплошные среды, имеющие конечные области определения, выделяемые в трехмерном геометрическом пространстве. Такие объекты представляют собой динамические системы с распределенными параметрами, их также называют непрерывными системами. Функционирование этих систем описывается дифференциальными уравнениями с частными производными.

На макроуровне объект проектирования рассматривают как динамическую

систему с сосредоточенными параметрами. Математическая модель макроуровня представляет собой системы обыкновенных дифференциальных уравнений

Целью курсовой работы в первой части является синтез интегральной передаточной функции для объектов управления с распределенными параметрами. В данной работе решается вопрос построения математической модели колебания мембраны на основе теории распределенных сигналов: по заданному дифференциальному уравнению объекта получить выражение для передаточной функции в распределенных параметрах, выражение для выходной величины, выражение для оценочной передаточной функции для наилучших условий управления. Необходимо построить оценочную ЛАЧХ, аппроксимировать ее и записать выражение передаточной функции через типовые звенья.

Во второй части курсовой работы необходимо построить графические и матричные формы математической модели заданной гидравлической системы, произвести расчет параметров ее элементов, расчет статического режима работы гидросистемы и осуществить анализ ее динамических свойств.

1 Моделирование на микроуровне

1. Исходные данные

Исходные данные для выполнения первой части курсовой работы:

1) Уравнение колебания струны /1/; с. 82:

(1)

2) Начальные условия:

,

3) Граничные условия:

, ;

0 ≤ x ≤ l, t ≥ 0, a ≠ 0

4) Стандартизирующая функция:

(2)

5) Функция Грина:

(3)

6) Континуальная передаточная функция:

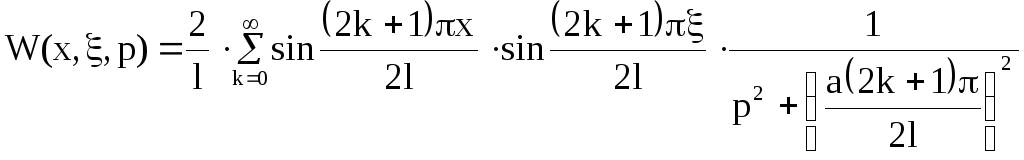(4)

2. Идентификация краевой задачи

Уравнение (1) представляет собой одномерное уравнение гиперболического типа, имеющее вторую производную по времени t. Данное уравнение описывает колебания струны. Проведём идентификацию всех величин, входящих в уравнение (1).

Дифференциальное уравнение имеет вид:

,

где Q(x,t) – выходная распределённая величина, представляющая собой ортого­-

нальную деформацию струны, [м];

f(x,t) – входное распределённое воздействие на струну, [м/c²].

Для уравнения (1) формулируются следующие условия:

– начальные условия: , ;

– граничные условия: , , 0 ≤ x ≤ l, t ≥ 0, a ≠ 0.

Стандартизирующая функция, компенсирующая влияние начальных и гра­ничных условий для данной одномерной задачи имеет вид (2).

Функция Грина, являющаяся решением краевой задачи при начальных и гра­ничных условиях и входном воздействии в виде δ-функции, имеет вид (3).

Континуальная передаточная функция, являющаяся преобразованием Лап­ласа функции Грина, имеет вид (4).

Для решения частной задачи примем следующие условия:

– входное воздействие:

f(x,t) = 0;

– начальные условия, описывающие положение струны и скорость в начальный момент времени:

,

;

– граничные условия, описывающие жесткое закрепление струны по длине:

,

, 0 ≤ x ≤ l, t ≥ 0, a ≠ 0.

Примем, что:

– а = 1 – волновая скорость струны;

– l = 1.5 [м] – длина струны;

– материал струны – сталь;

– ρ = 7.8 · 10³ – плотность стали.

Представим на рисунке 1 изображение струны в начальный момент времени:

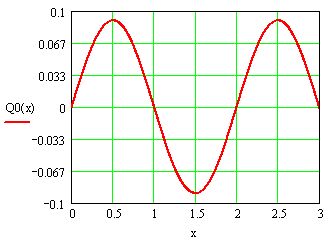
Рисунок 1 – Изображение струны

Отобразим на рисунке 2 изображение изменения внешнего воздействия во времени:

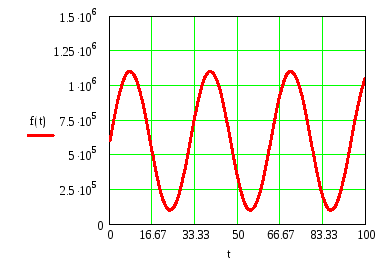
Рисунок 2 – Изображение изменения внешнего воздействия во времени

Произведём проверку размерности.

Пусть Q(x,t) – ортогональное отклонение струны [м]. Тогда входное воздействие f(x,t) имеет размерность [м/с²]:

,

где p – давление на струну, [Н/м²];

ρ – плотность материала струны, [кг/м³];

l – длина струны, [м].

Тогда:

.

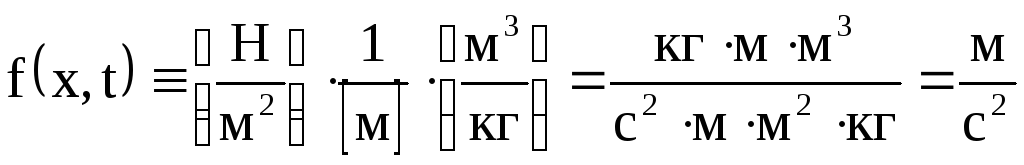Волновая скорость струны а имеет размерность [м/с]:

,

где T – натяжение струны, [Н/м²];

ρ – плотность материала струны, [кг/м³].

Тогда:

.

Учитывая размерности всех коэффициентов и величин, входящих в данное урав­нение, получим:

,

.

Размерность соблюдается, следовательно, все коэффициенты подобраны – верно.

С учётом входного воздействия, принятых начальных и граничных условий стандартизирующая функция принимает вид:

,

где δ^'(t) – импульсная переменная функция.

3. Расчёт выходной распределенной величины

Идентификация исходного уравнения позволяет перейти к расчету распреде­ленной выходной величины, являющейся функцией как пространственной, так и временной координаты и рассчитываемой как пространственно-временная компози­ция от произведения функции Грина на стандартизирующую функцию:

(5)

Выходная величина Q(x,t) находится как сумма двух составляющих:

Q(x,t)=Q₁(x,t) + Q₂(x,t), (6)

где Q₁(x,t) и Q₂(x,t) – первая и вторая составляющие выходной величины и находятся как:

(7)

(8)

Первая составляющая решения выходной функции:

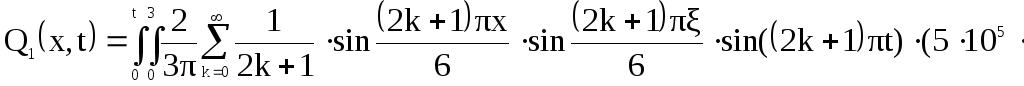
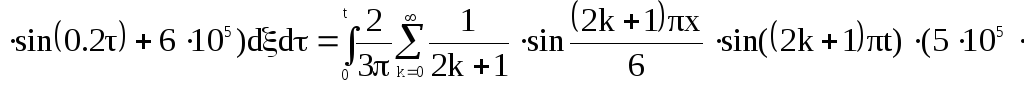
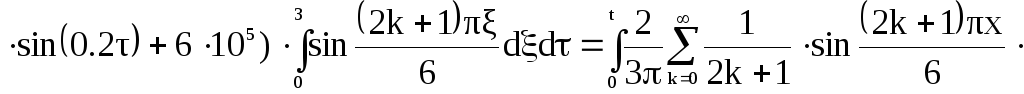
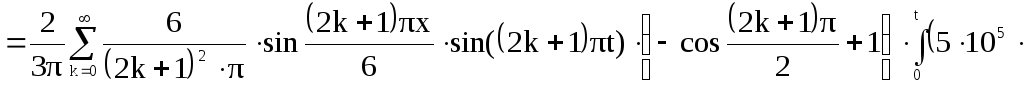
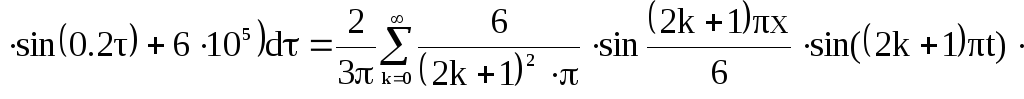
(9)

Вторая составляющая решения выходной функции:

(10)

Определим производную функции Грина:

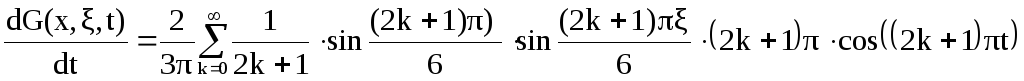
Подставим выражение найденной производной в (10):

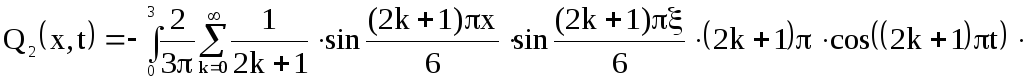
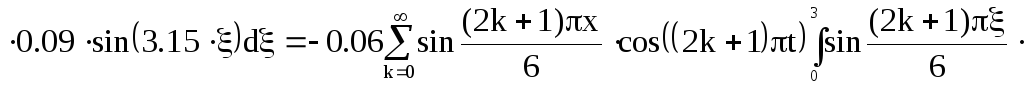
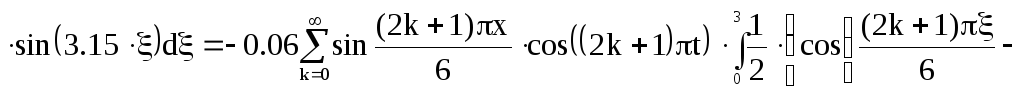
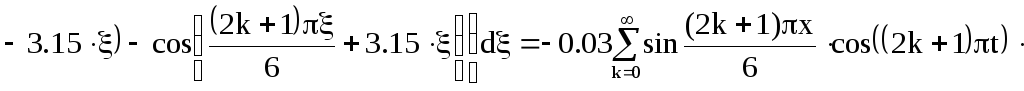
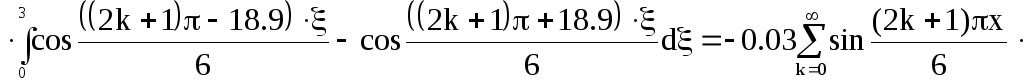
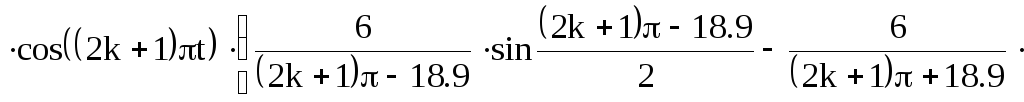
(11)

Выходная величина:

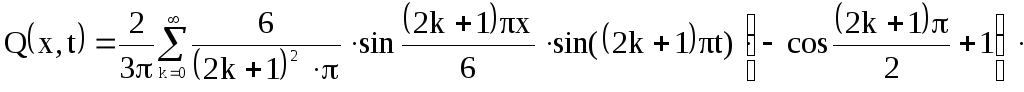
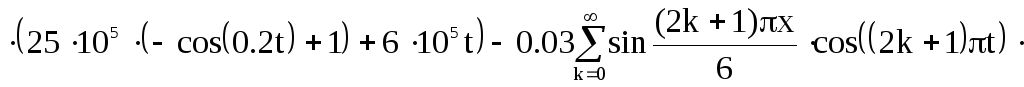
Построим график этой функции при фиксированном времени t:

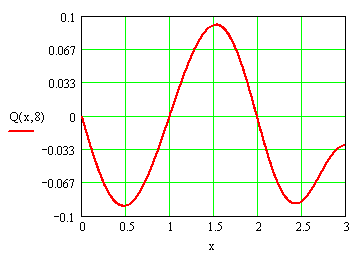
Рисунок 3 – График выходной величины Q(x,t) при t = 8 с.

Полученный в результате расчета выходной распределенной величины график не соответствует исходным данным, а именно: граничным условиям, т.к. один конец струны находится в свободном движении, а не жестко закреплен, как это было задано изначально. Такое несоответствие можно объяснить погрешностью вычислений или же неправильно подобранными значениями исходных данных.

4. Расчет интегральной передаточной функции

Динамическая характеристика находится по интегральной передаточной функции , которая рассчитывается как пространственная композиция от произведения континуальной передаточной функциина преобразованную по Лапласу стандартизирующую функциюс выделенным из нее входным воздействием.

Стандартизирующая функция содержит входное воздействие f(x,t) и имеет вид:

Произведем преобразование Лапласа стандартизирующей функции:

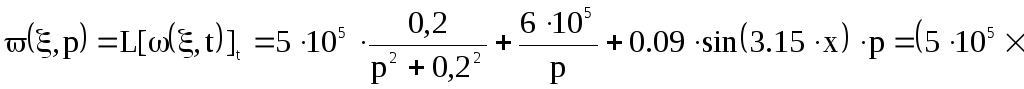
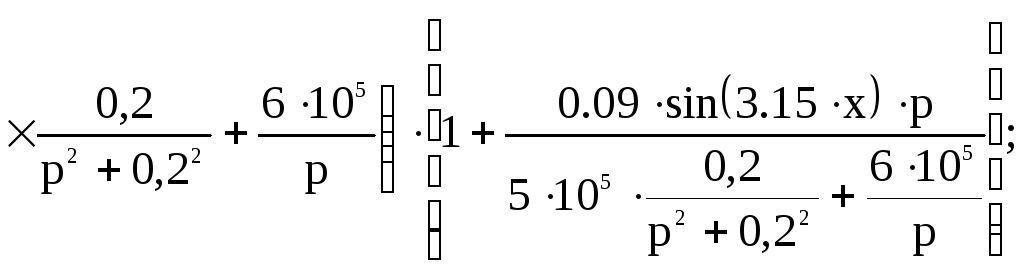
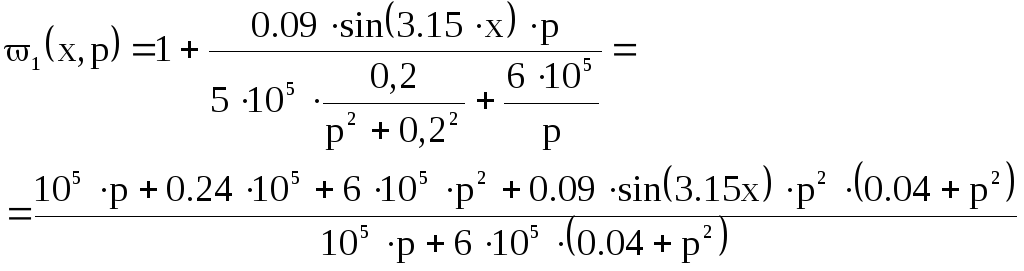
Интегральная передаточная функция:

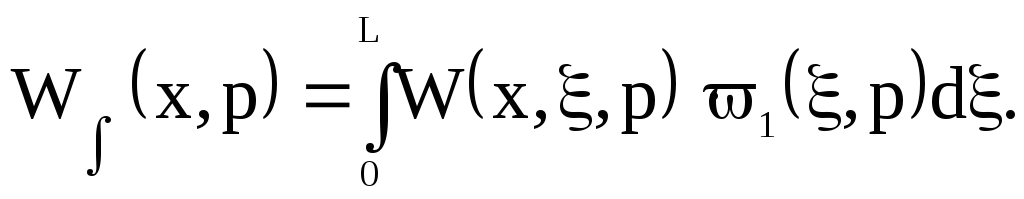
Континуальная передаточная функция:

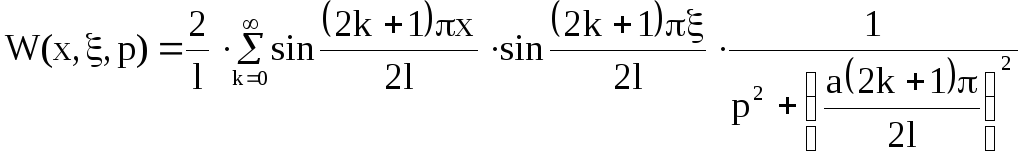
Интегральную передаточную функцию найдем как:

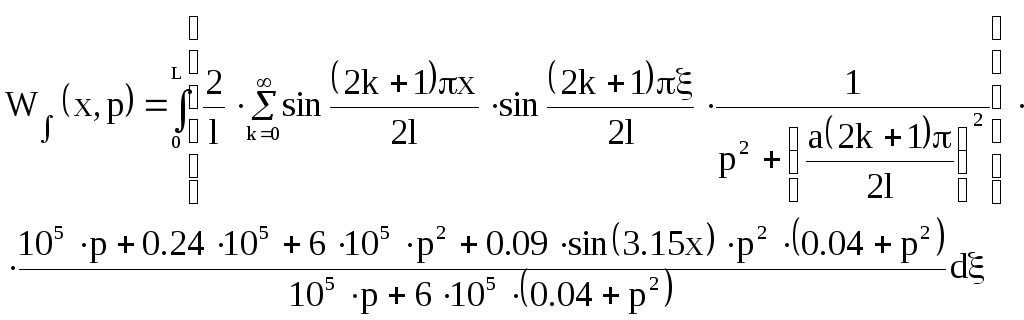
Подставим значения и получим:

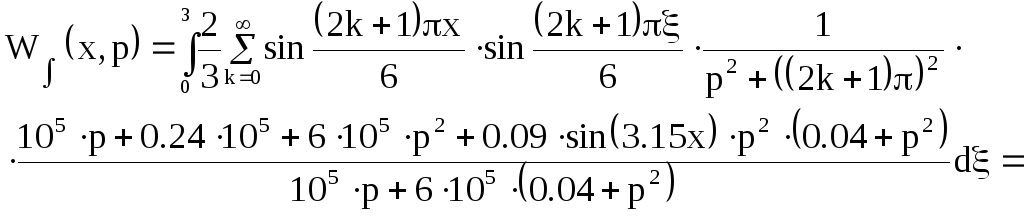
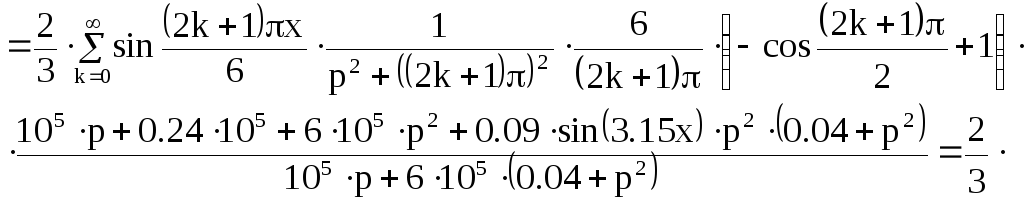
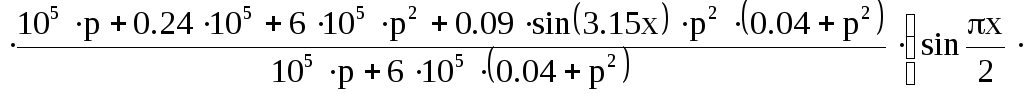
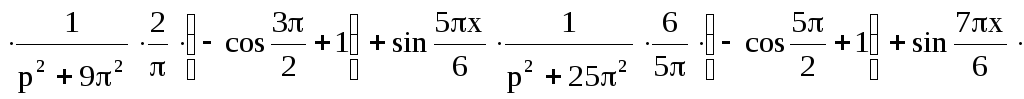
(12)

Для построения ЛАЧХ необходимо подставить значение в выражение (12) и получить частотную форму записи интегральной передаточной функции, для чего произведем заменуp = jω:

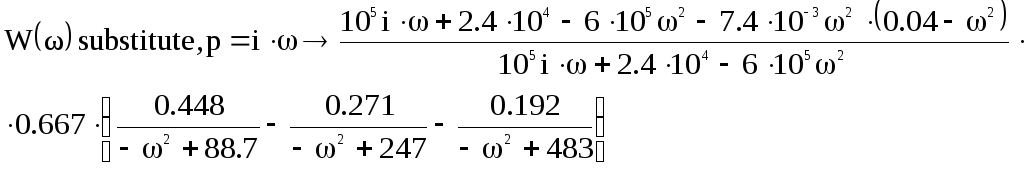
Для построения характеристики используем программу MathCad.