
курсовая работа / ЗАДАНИЕ
.DOCМинистерство общего и специального образования Российской Федерации
Саратовский государственный технический университет
Балаковский институт техники, технологии и управления
Кафедра УИТ
Курсовая работа
по дисциплине «Моделирование систем управления»
Выполнил студент группы УИТ - 41
Жалилина Ю. А.
Проверил преподаватель
Фролова М. А.
1999
Задание.
По заданному дифференциальному уравнению получить выражение для передаточной функции в распределенных параметрах, выражения для выходной величины, для оценочной передаточной функции для наилучших условий управления. Построить оценочную ЛАЧХ, аппроксимировать ее с погрешностью 5% инерционно-форсированными звеньями и записать выражение передаточной функции через типовые звенья.
![]() (1)
(1)
начальные условия:![]() ,
,
![]() ;
;
граничные условия:
![]()
![]()
![]() ;
;
![]()
![]() (2)
(2)
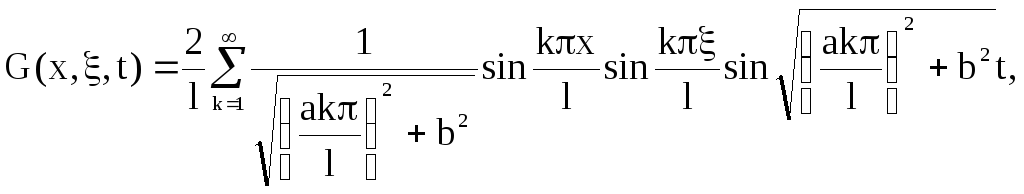 (3)
(3)
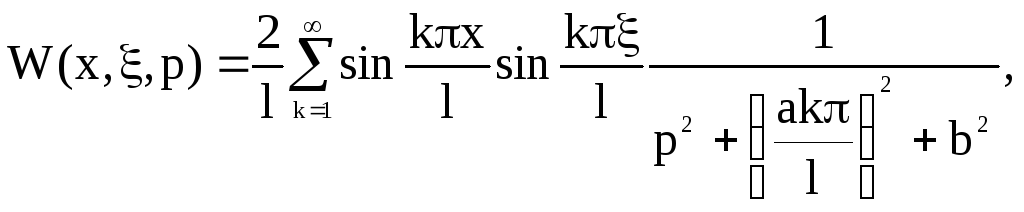 (4)
(4)
Решение.
По виду уравнения определяем, рассматриваемый процесс можно идентифицировать, как продольные колебания стержня, концы которого движутся по заданному закону:
Пусть начальные условия нулевые:
![]() ,
,
![]() ;
;
Зададим граничные
условия. Пусть один конец жестко
закреплен:
![]() а второй движется по заданному закону:
а второй движется по заданному закону:![]() ,
а
,
а
![]() .f(x,t)=Fsint,
.f(x,t)=Fsint,
Тогда нормирующая функция (2) будет иметь вид:
![]()
Учитывая свойство
![]() получим:
получим:
![]()
Найдем вариации отклонения:
![]() (5)
(5)
Используя выражение (3) получим:
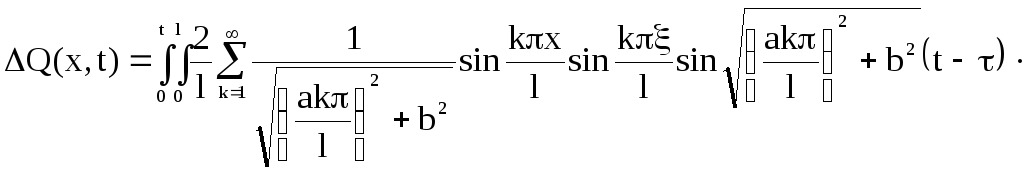
![]()
Преобразуем (5) по Лапласу:
![]() (6)
(6)
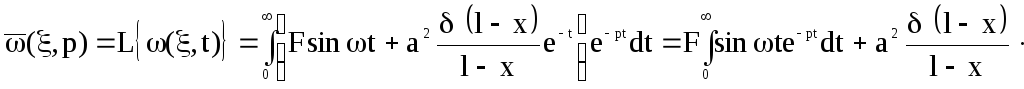 .
.![]()
По таблице преобразования Лапласа вычисляем интегралы, тогда получим:
![]() .
.
Представим
![]() в виде двух множителей:
в виде двух множителей:
![]() .
.
Подставляя
![]() ,
получим выражение изображения по Лапласу
выходной функции
,
получим выражение изображения по Лапласу
выходной функции
![]()
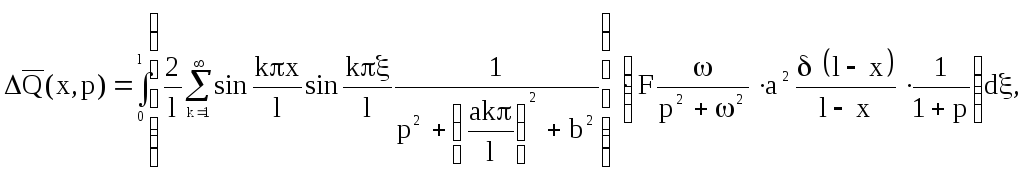
Выносим
за скобку
![]() :
:
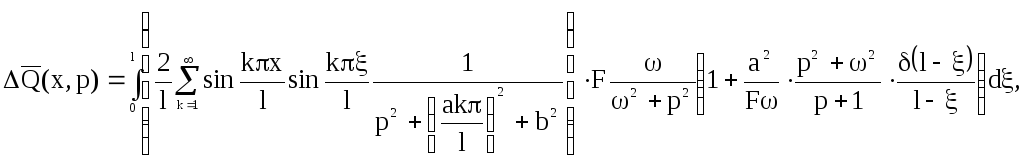
Находим интегральную передаточную функцию:
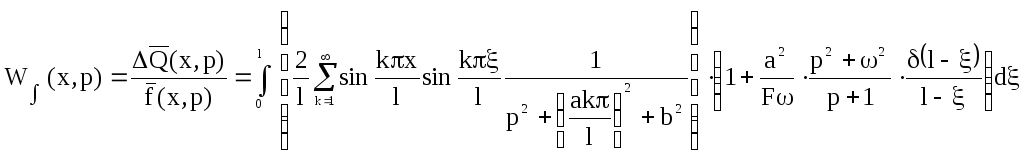
Разбиваем интегральную передаточную функцию на два интеграла и решим их с помощью программы MathCad 8:
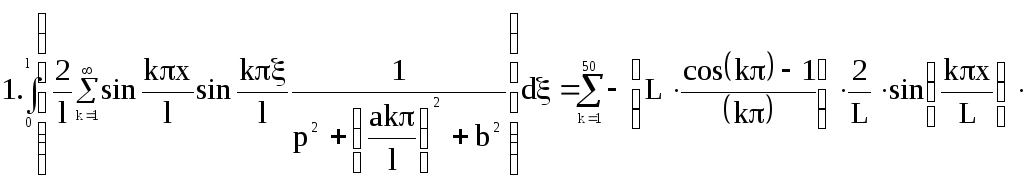
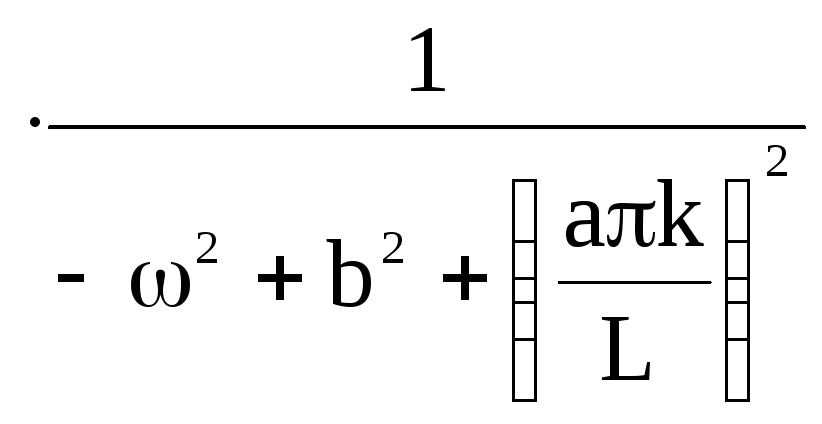
2.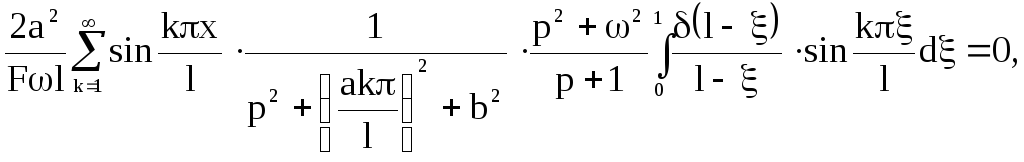
т.к.
при замене p на
![]() получаем :
получаем :![]()
Окончательно интегральная передаточная функция имеет вид:
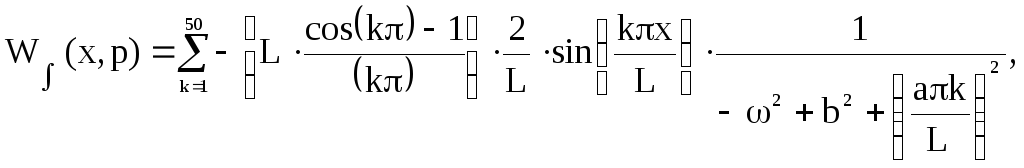
т.е. первому интегралу, решенному в программе MathCad 8
Заменим
р на j
и с помощью программы MathCad 8
строим оценочную ЛАЧХ при х = 1,9;
L=2; b=1; a=1;![]() ,
,
![]() ,
,
которая представлена на рис. 1.
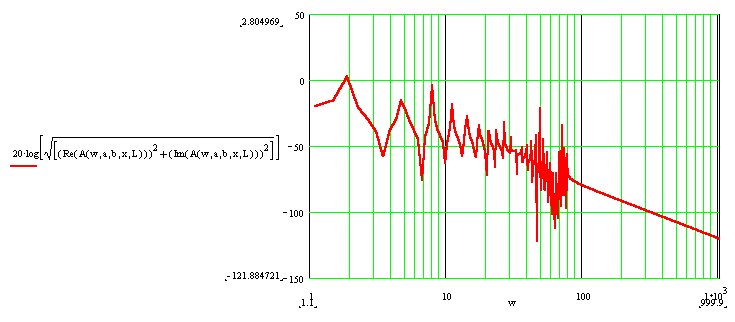
Рис. 1. Оценочная ЛАЧХ.
Данная ЛАЧХ имеет сложный характер, поэтому аппроксимировать ее не представляется возможным.
