курсовая работа / 2 РАСЧЕТ ИНТЕГРАЛЬНОЙ ПЕРЕДАТОЧНОЙ ФУНКЦИИ СРП

2 РАСЧЕТ ИНТЕГРАЛЬНОЙ ПЕРЕДАТОЧНОЙ ФУНКЦИИ СРП

ЗАДАНИЕ

Необходимо представить устройство (индуктивный датчик) как систему элементарных звеньев и рассмотрев один из блоков, по заданному дифференциальному уравнению получить его выражение для передаточной функции в распределенных параметрах, выражение для выходной величины, выражение для оценочной передаточной функции для наилучших условий управления. Построить оценочную ЛАЧХ, аппроксимировать ее и записать выражение передаточной функции через типовые звенья.

Дифференциальное уравнение:

Начальное условие:

,

, ,

Функция Грина: ;

Нормирующая функция:

2.1 ОБЩИЕ СВЕДЕНИЯ ОБ ОСНОВНЫХ ХАРАКТЕРИСТИКАХ СИСТЕМ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

Система с распределенными параметрами (СРП) – это система, в которой практически все сигналы (особенно входной и выходной) зависят от пространственных координат и времени.

Есть среды, которые не могут быть описаны в сосредоточенных параметрах (электромагнитное поле, электростатическое поле, течение потока, гравитационное поле, температура и т.д.).

Система с сосредоточенными параметрами является частным случаем СРП и вводится для упрощения и решения задач на первом (нулевом) этапе.

Основной характеристикой СРП является континуальная передаточная функция. Она показывает отношение выходной функции к входной (по Лапласу) в привязке к конкретной точке.

В искомой задаче выходная функция будет обозначаться буквой Q(x, t), где x – трехмерная переменная в декартовых, цилиндрических или сферических координатах.

f(x,t) – входная координата по среде, зависящая от трехмерной координаты x и времени t.

Основное уравнение задачи записывается в виде:

где l – так называемый оператор дифференциального уравнения – это формула преобразования выходной величины Q.

В каждой задаче определяются граничные или краевые условия:

где Г – оператор граничных или краевых условий;

g – входное воздействие на границе в каждый момент времени;

Для того, чтобы решить задачу во всей области координат, необходимо знать ее значения в каждой точке по границе области.

Начальные условия для задачи записываются в виде:

где N – оператор начальных условий;

Q₀ (x) – значение искомой функции в заданный момент времени t₀ в каждой точке пространства x.

Получили систему:

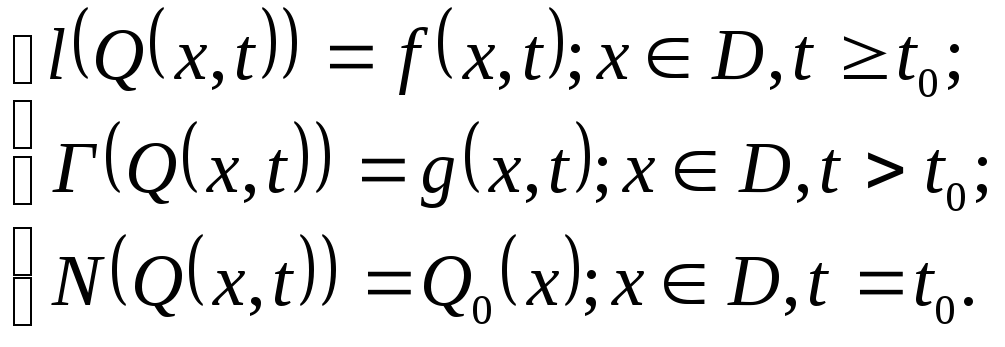
Необходимо знать:

1. Значение функции на границе в каждый момент времени.

2. Значение в каждой точке области в момент времени t₀.

В указанном виде система практически не разрешима. Вводится в рассмотрение так называемая стандартная форма записи. Она подразумевает нулевые граничные и начальные условия. Ее вид:

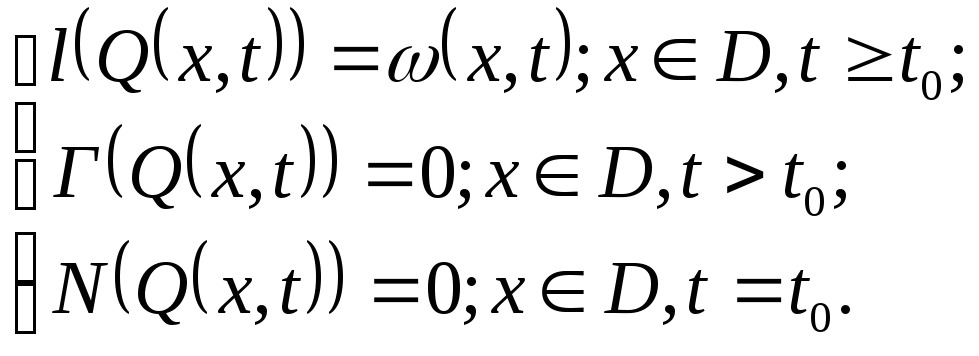
где (x, t) – стандартизующая функция.

Второй функцией является функция Грина (импульсная переходная функция, функция влияния, функция источника, функция веса).

Функцией Грина называется функция источника, которая равна выходному сигналу:

,

при ,

где - пространственная  - функция по координатам x, y, z.

-  - функция по времени;

x – координаты входного возмущения;

 - координаты точки отклика от удара.

С учетом этого стандартная задача (2) перепишется в виде:

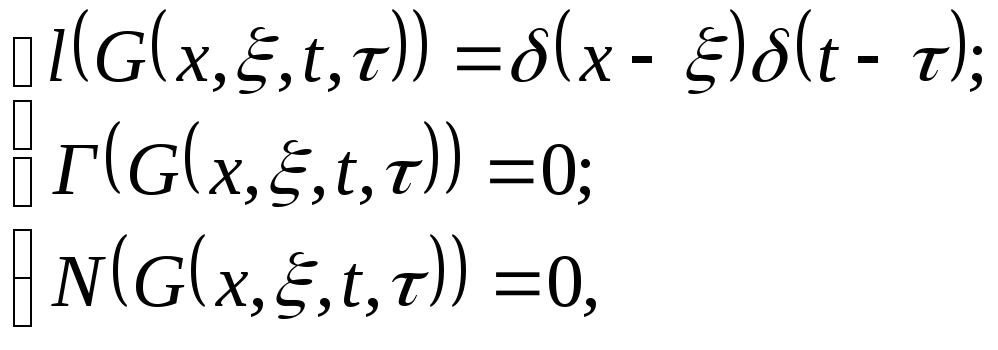
где функция Грина от G(x, t) берется из справочника и является второй основной характеристикой.

Зная эти две характеристики можно найти выходную функцию по следующему выражению:

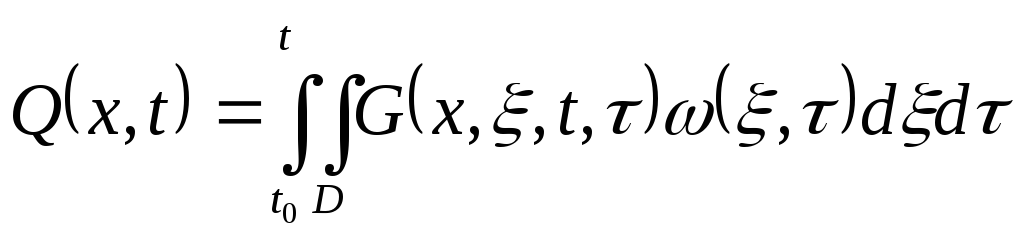
Если задача статическая, тогда отсутствует уравнение времени t. Бывают задачи, в которых отсутствуют пространственные координаты, т.е. процесс во времени.

Для управления и синтеза системы управления, исходя из ТАУ, необходимо знать передаточную функцию. В теории СРП вводится понятие так называемой континуальной передаточной функции, т.е. точечной передаточной функции, в пределах области D, когда возмущение подается на среду в точке x функциями: и , а реакция регистрируется в точке .

Континуальная передаточная функция выражается следующим образом:

.

По сути, континуальная передаточная функция – это преобразование Лапласа функции Грина, т.е. при этих функциях континуальная передаточная функция является производной и всегда может определиться по функции Грина.

Таким образом, для решения задачи по СРП необходимо знать две функции: нормирующую функцию и функцию Грина.

Теория СРП включает структурный метод ТАУ, который подразумевает операции с распределенными блоками:

1. блоки соединяются последовательно;

2. блоки соединяются параллельно;

3. включение второго блока в обратную связь.

В связи с этим вводится понятие операторного изображения выходной величины. В теории распределенных блоков выходная величина определяется следующим образом:

,

где - изображение по Лапласу выходной величины решаемой задачи;

- континуальная передаточная функция;

- изображение по Лапласу нормирующей функции.

Если удается из нормирующей функции выделить в явном виде компоненту входной координаты с помощью специальных средств или методов

,

то уравнение для перепишется в виде:

С помощью двух способов (коэффициент разложения и коэффициент приближения) по возможности выносится входное возмущение (по Лапласу) за знак интегрирования, имеем:

.

Полученное выражение – отношение изображения по Лапласу выходной величины к изображению по Лапласу входного возмущения, как интеграл по области D континуальных функций, называется интегральной передаточной функцией (функция Власова В.В.).

2.2 ПРЕДСТАВЛЕНИЕ УСТРОЙСТВА КАК СИСТЕМУ ЭЛЕМЕНТАРНЫХ ЗВЕНЬЕВ

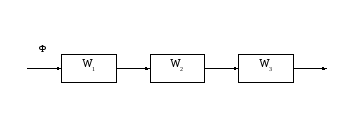
Рисунок 2 – Индуктивный датчик представленный виде системы элементарных звеньев

W₁ – сопло, где входным сигналом является поток жидкости скоростью υ, выходной сигнал - υ' (из-за формы сопло, скорость потока жидкости на выходе меняется);

W₂ – жидкость внутри сильфона, где р_у – давление удара, которое передается через центральное отверстие в перегородке;

W₃ – пространство с наружи сильфона, где р_с – статическое давление потока, которое передается жидкости во время протекания ее по выходному штуцеру;

2.3 CИНТЕЗ ИНТЕГРАЛЬНОЙ ПЕРЕДАТОЧНОЙ ФУНКЦИИ ДЛЯ

ОБЪЕКТОВ УПРАВЛЕНИЯ

Рассмотрим решения данного дифференциального уравнения для входного сопла W₁, на вход которого подается жидкость, характеризующаяся скорость υ [м/сек.], а на выходе имеем скорость υ' [м/сек.].

Т.к. скорость измеряется в м/с, то возникает необходимость в коэффициенте, стоящем перед первым слагаемым ДУ, который измеряется в cек.

а – коэффициент, измеряемый в сек, а=1 с.

В соответствии с установленными ограничениями размерностей коэффициентов, размерности входного и выходного сигнала совпадают.

Для дальнейшего расчета необходимо провести идентификацию выходной величины Q и входного возмущения f.

Зададим входное воздействие: - поток жидкости, протекающий по входному сопло.

Координаты точки, в которой необходимо отыскать выходную величину Q как функцию отклика на возмущение, ζ изменяется в пределах 0<ζ<L (что соответствует длине сопло), а η – будет изменятся в пределах 0<η<R (ширина сопло).

Q – выходная величина, соответствующая скорости жидкости после протекания ее через сопло.

В соответствии с этими допущениями начальные условия запишутся в виде:

Тогда нормирующая функция примет вид:

Выходная величина записывается в виде:

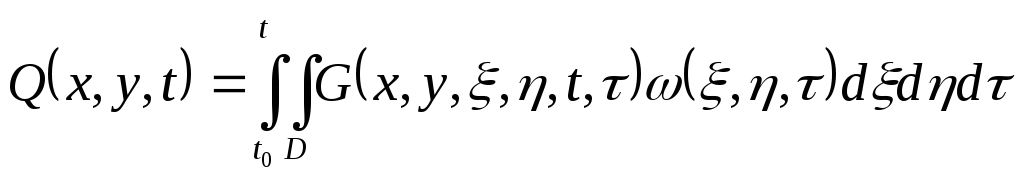
Подставим выражение для функции Грина и нормирующей функции , получим:

Для определения интегральной передаточной функции необходимо найти операторное выражение выходной величины, которое будет иметь вид:

,

где - континуальная передаточная функция;

- изображение по Лапласу нормирующей функции.

Найдем изображение по Лапласу нормирующей функции:

,

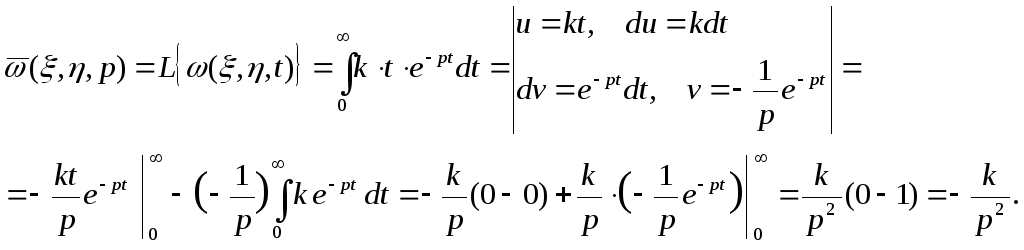
Для дальнейших вычислений необходимо определить континуальную передаточную функцию по формуле:

,

Т.е.:

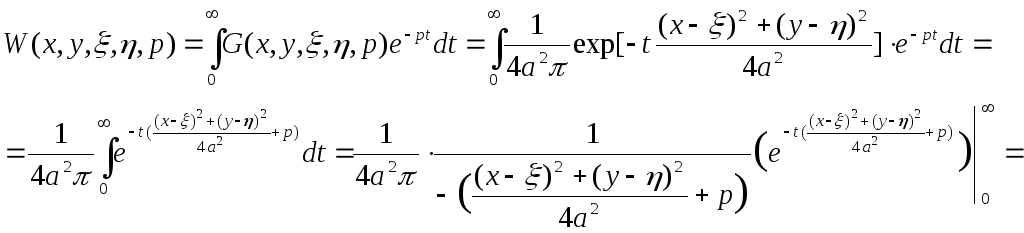
Таким образом, операторное изображение выходной величины запишется:

.

Интегральная передаточная функция записывается в следующем виде:

,

т.к. ,), Следовательно:

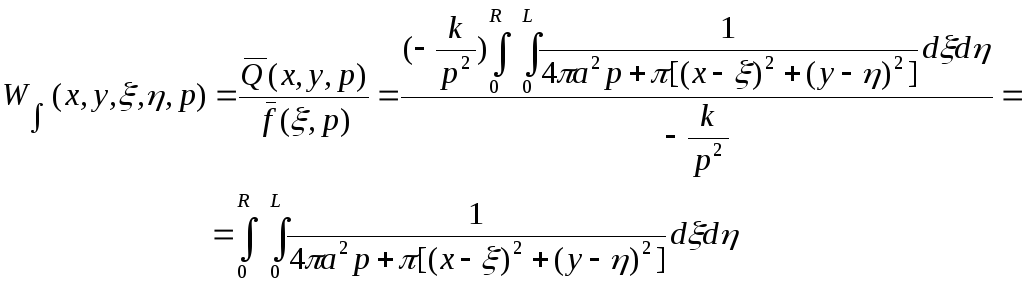
Для конкретного случая переменную ξ ограничим длиной рассматриваемого сопло L=6м, т.е. 0<ζ<6, а переменную η – ограничим шириной данного сопла R=1м (0<η<1). При х=0, у=0 имеем:

.

Дальнейшее решение интегральной передаточной функции будем вести с помощью программы Matchcad 2000.

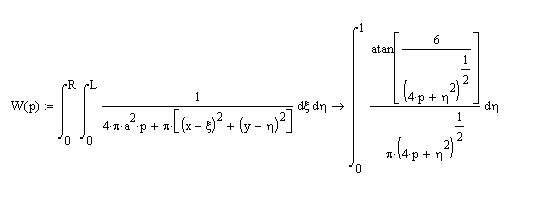
Для того, что бы решить получившийся интеграл, необходимо выражение

разложить в ряд относительно η. Получим: Возьмем интеграл от каждого члена этого ряда в отдельности.

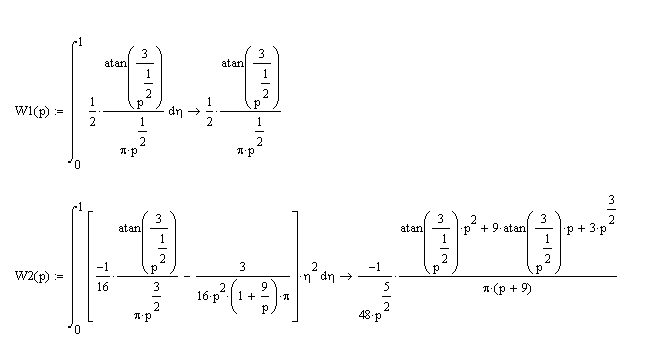
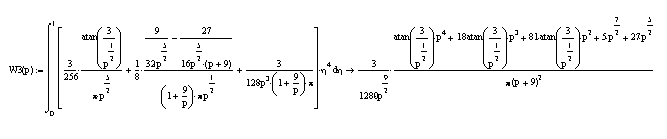
Тогда интегральная передаточная функция принимает вид:

Для построения ЛАЧХ и ФЧХ необходимо перейти от операторной формы записи передаточной функции к передаточной функции, записанной в изображениях по Лапласу. А после получить частотную форму записи передаточной функции, для этого произведем замену р= j.

Выделим в полученном выражение действительную и мнимую части, и воспользуемся следующими формами для нахождения ЛАЧХ и ЛФЧХ:

;

.

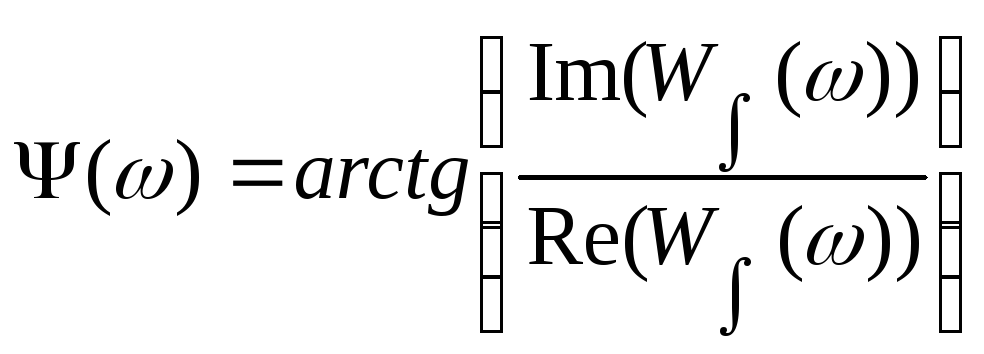При проведении аппроксимации определим сопрягающиеся частоты.

ω = 1 → T = 1/ω = 1.

20lg k =-14 , откуда k = 10 ^{(-14 / 20)} = 0,1995 – статический коэффициент передачи.

С помощью аппроксимации передаточная функция запишется в виде:

В результате аппроксимации получили произведение интегрирующего и апериодическое звено первого порядка.