курсовая работа / Пример синтеза интегральной передаточной функции СРП

Пример синтеза интегральной передаточной функции СРП.

Исходные данные:

;

;

;

;

; ; ;

; ;

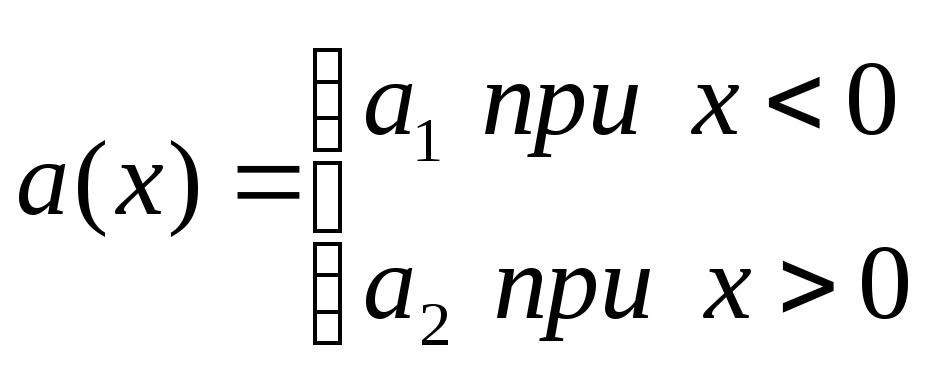где а_1­ и а₂ – коэффициенты температуропроводности;

;

;

; ; ; -

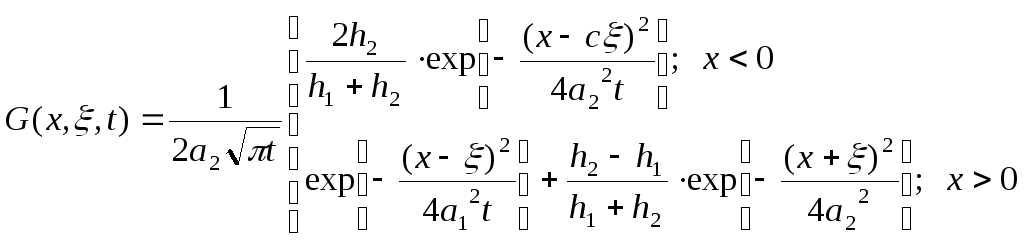температура неограниченного составного стержня;

;

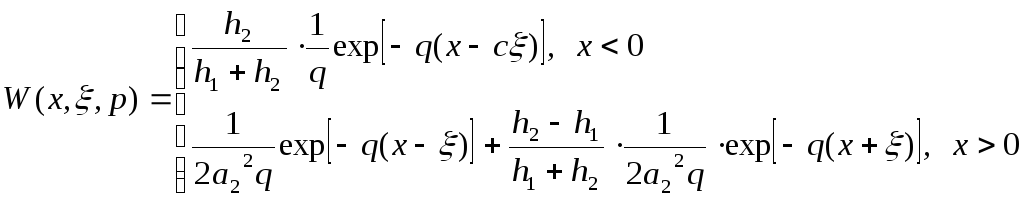В начале расчета необходимо провести идентификацию выходной величины Q, входного возмущения f и координат x, t .

Входным возмущением f(x, t) является поток тепла от нагревательного элемента, приложенного к стержню в точке 0.

.

 - координата точки, в которой необходимо отыскать выходную величину Q как функцию отклика на возмущение,  изменяется в пределах -    +.

Q – выходная величина, соответствующая температуре стержня после воздействия на него теплового потока.

Начальные условия с учетом этих допущений запишутся в виде:

, что соответствует температуре окружающей среды, которая равна температуре стержня в начальный момент времени.

Граничные условия заданы в виде пределов:

, при А = const = 100⁰ C;

;

;

отсюда, , где  - коэффициент теплообмена.

;

где k – коэффициент теплопроводности, зависящий от материала стержня;

с – удельная теплоемкость тела;  - плотность среды. а₁ = а₂ = 1.

Таким образом, выходная величина запишется в виде уравнения :

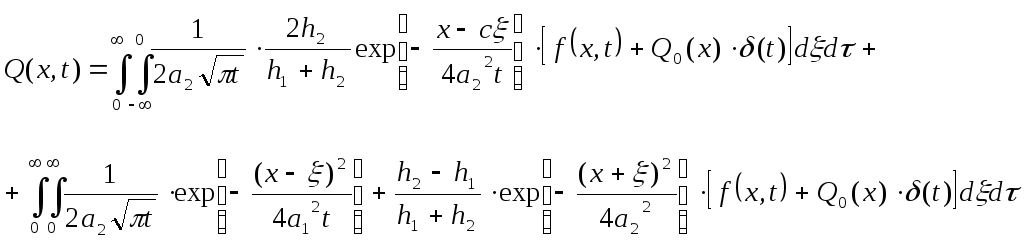Нормирующая функция

Для определения интегральной передаточной функции необходимо найти операторное выражение выходной величины, которое будет иметь вид выражения (14).

Континуальная передаточная функция примет вид:

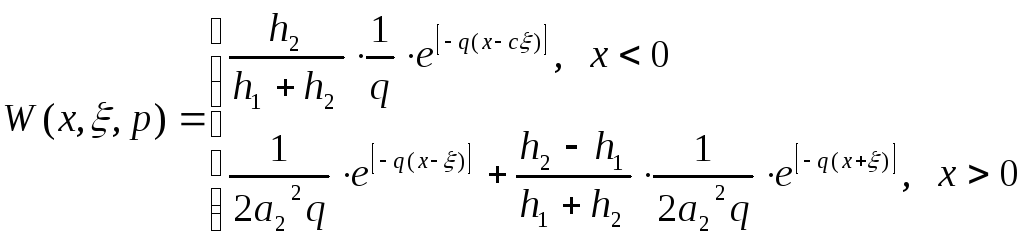При подстановке исходных данных h₁=h₂=1, , a₂=1:

;

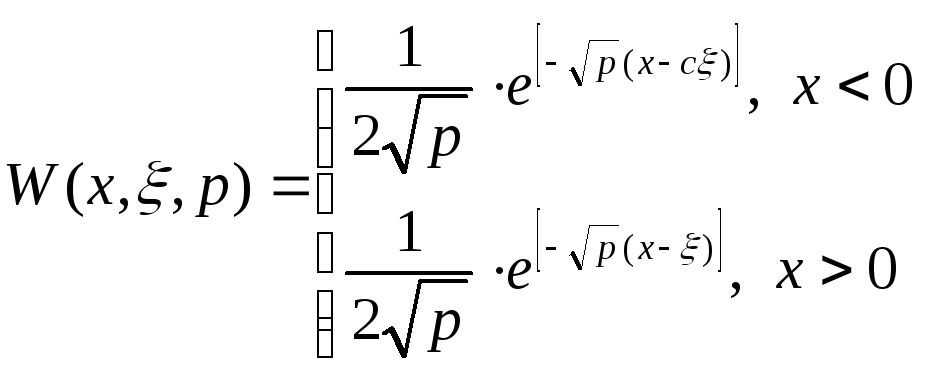
Таким образом, при изменении континуальная передаточная функция равна

Для дальнейших вычислений необходимо определить изображение по Лапласу нормирующей функции по формуле (15)

;

;

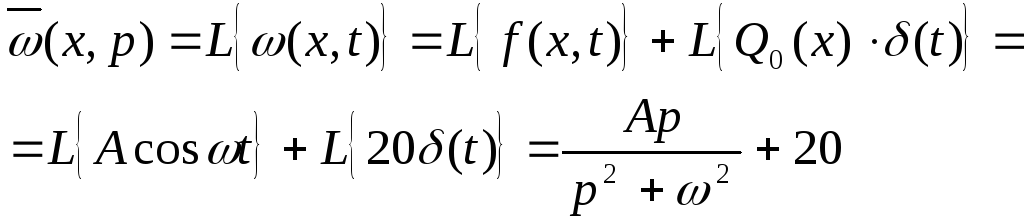Таким образом, операторное изображение выходной величины запишется:

;

интегральная передаточная функция перепишется в виде:

Для конкретного случая рассматривается стержень ограниченной длины, следовательно,  изменяется в пределах от 0 до 10.

Таким образом, передаточная функция запишется в виде:

;

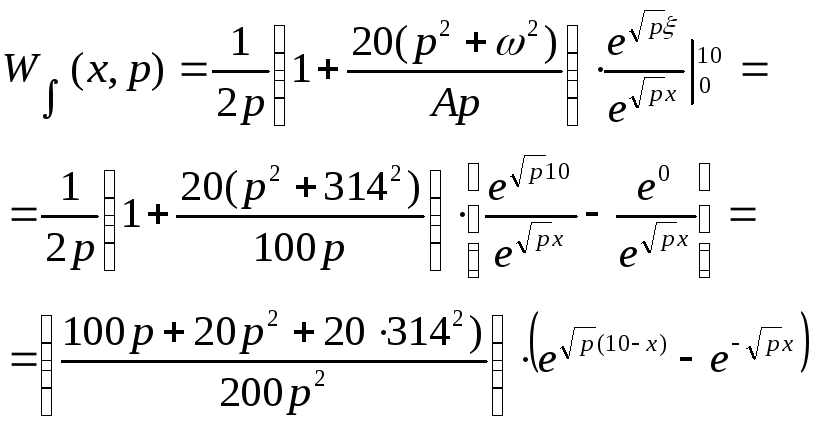При замене оператора р на j, выражение будет:

;

Разделив полученное выражение на действительную и мнимую части:

;

.

По полученным данным строим графики ЛАЧХ и ФЧХ (рисунки 1 и 2).

;

.

При проведении аппроксимации сопрягающие частоты будут:

;

;

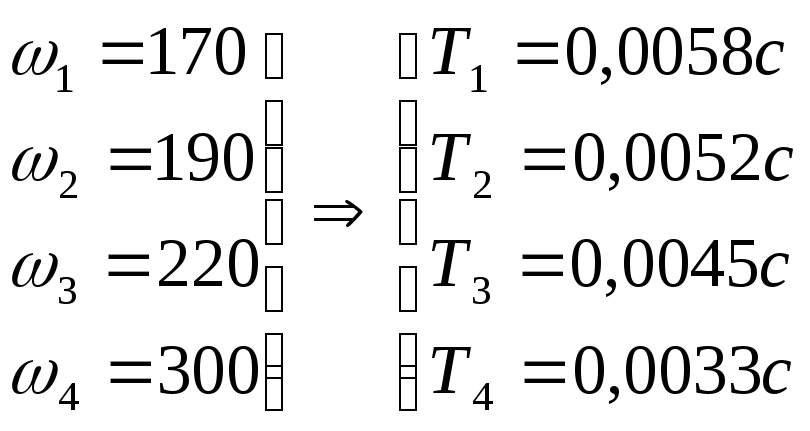С помощью аппроксимации передаточная функция запишется в виде:

На рисунке 1 показаны фактическая L() и аппроксимированная N() ЛАЧХ.

Для построения ЛФЧХ:

На рисунке 2 изображены фактическая () и аппроксимированная () ЛФЧХ.

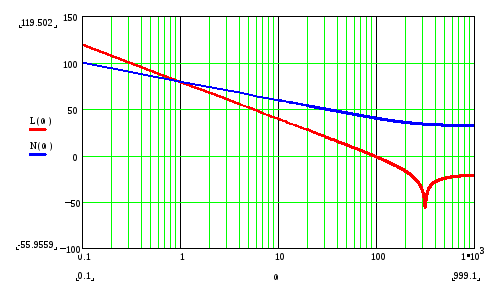
Рисунок 1 – Логарифмическая амплитудно-частотная характеристика (фактическая и аппроксимированная)

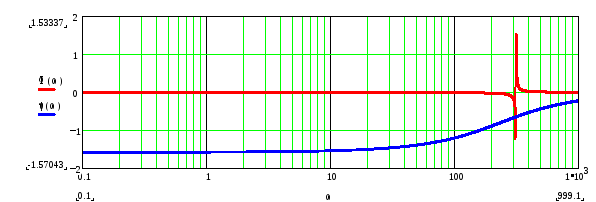
Рисунок 2 – ЛФЧХ системы (фактическая и аппроксимированная)