курсовая работа / Уравнения матфизики

2 . ОСНОВНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ

Уравнения гиперболического типа

2.1 Уравнения поперечных колебаний струны

Рассмотрим струну длиной l, которая в положении равновесия находится вдоль оси Ох. Ее поперечные колебания в каждый момент времени t для каждой точки х (0≤х≤l) характеризуется вектором смещения Q(x,t) и описывается уравнением вида:

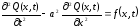, (2.1)

где а – волновая скорость, м/с;

f(x,t) – удельная сила (сила, действующая на единицу массы струны), м/с².

Волновая скорость определяется согласно выражению:

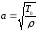, (2.2)

где Т₀ – сила натяжения струны, Н;

ρ – линейная плотность (масса, приходящаяся на единицу длины струны), кг/м.

Удельная сила, в свою очередь, может быть представлена в виде:

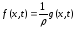, (2.3)

где g(x,t) – линейная плотность внешней силы, Н/м.

Если внешней силы нет f(x,t)=0, получаем уравнение свободных колебаний струны:

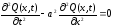. (2.4)

Для выбора начальных условий к данной задаче необходимо задать:

- профиль начальных смещений струны:

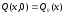; (2.5)

- профиль начальных скоростей:

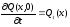. (2.6)

Также необходимо задать граничные условия (условия на концах струны).

1) Если концы струны закреплены, то имеем следующие граничные условия:

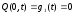; (2.7)

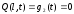. (2.8)

2) Если концы струны свободны, т.е. могут свободно перемещаться по прямым, параллельным направлению отклонения Q(x,t), то граничные условия имеют вид:

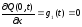; (2.9)

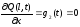. (2.10)

3) Если концы струны закреплены упруго, т.е. каждый конец испытывает со стороны заделки сопротивление, пропорциональное отклонению и направленное противоположно ему, то ГУ:

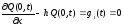; (2.11)

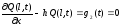, (2.12)

где h=k/T₀;

k – коэффициент упругости упругого закрепления концов струны.

4) Если концы струны двигаются в поперечном направлении по заданным законам, то ГУ:

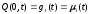; (2.13)

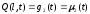, (2.14)

где μ₁(t), μ₂(t) - определяют закон движения концов.

Пример 1.

Движение струны, натянутой и закрепленной в двух точках на расстоянии l, начинается посредством смещения струны в положение у=a·sin(πx/l), из которого струну отпускают в момент времени t=0. Сформулировать краевую задачу для данного условия.

Функция Q(x,t), описывающая поперечные смещения струны определяется уравнением:

.

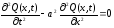Поскольку концы струны закреплены, имеем граничные условия вида (2.7), (2.8):

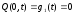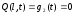; . Начальные условия представляются в виде:

;

.

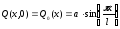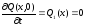Пример 2.

Сформулировать краевую задачу о колебаниях однородной струны (0<x<l), закрепленной на концах, под действием внешней непрерывно распределенной силы с плотностью g(x,t)=Asin(ωt), где ω≠(kπa/t) (k=1,2…). Начальные условия нулевые.

Функция Q(x,t), описывающая колебания струны определяется уравнением:

,

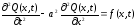где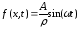

Поскольку концы струны закреплены граничные условия нулевые:

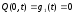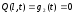; . Начальные условия по условию задачи также равны нулю:

;

.

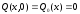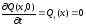Пример 3.

Сформулировать краевую задачу о вынужденных поперечных колебаниях струны, закрепленной на одном конце (х=0) и подверженной на другом конце (x=l) действию возмущающей силы, которая вызывает смещение, равное А·sin(ωt), где ω≠(kπa/t) (k=1,2…). В момент времени t=0 смещения и скорости равны нулю.

Функция Q(x,t), описывающая вынужденные колебания струны определяется уравнением:

.

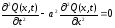Начальные условия:

;

.

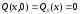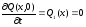Граничные условия задаются в виде:

;

.

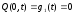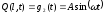2.2 Уравнения продольных колебаний стержня

Рассмотрим стержень длиной l, который в положении равновесия находится вдоль оси Ох. Его продольные колебания описываются функцией Q(x,t), представляющие собой в каждый момент времени t продольное смещение точки стержня, координата которой в положении равновесия была равна х. Предполагается, что натяжение в стержне подчиняется закону Гука. Тогда уравнение, описывающее продольное колебание стержня имеет вид:

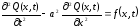, (2.15)

где а – волновая скорость, м/с;

f(x,t) – удельная сила, м/с².

Волновая скорость стержня определяется согласно выражению:

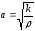, (2.16)

где k – коэффициент упругости, Н;

ρ – линейная плотность (масса, приходящаяся на единицу длины стержня), кг/м.

Коэффициент упругости k может быть найден следующим образом:

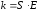, (2.17)

где S – площадь поперечного сечения стержня, м²;

Е – модуль Юнга (напряжение, возникающее в образце при увеличении (уменьшении) его длины в два раза при прочих неизменных условиях), Н/м².

Для однородного стержня k=const, ρ=const. В противном случае k(х), ρ(х).

Удельная сила, в свою очередь, может быть представлена в виде:

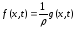, (2.18)

где g(x,t) – линейная плотность продольной внешней силы (сила, действующая на единицу длины), Н/м.

Начальные условия задаются в виде:

- профиля начальных смещений:

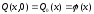; (2.19)

- профиля начальной скорости:

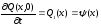. (2.20)

Граничные условия могут быть заданы для следующих случаев:

1) Первая краевая задача (граничные условия 1 рода):

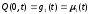; (2.21)

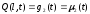, (2.22)

где μ₁(t), μ₂(t) – заданные функции времени, описывающие закон

движения конца стержня.

Для жестко закрепленного конца μ(t)=0.

2) Вторая краевая задача (граничные условия).

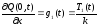; (2.23)

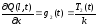, (2.24)

где T₁, T₂ – сила натяжения, приложенная к концу стержня, Н.

В случае свободного конца, натяжение стержня вблизи него отсутствует (g(t)=0).

3) Третья краевая задача (граничные условия 3 рода).

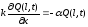. (2.25)

Данные условия формулируются в случае упругого закрепления стержня, при котором конец стержня может перемещаться, но возникает упругая сила, стремящаяся вернуть сместившийся конец в прежнее положение.

Пример.

Сформулировать краевую задачу о продольных колебаниях однородного цилиндрического стержня, один конец которого заделан, а к другому концу приложена сила F=A·sin(ωt), направление которой совпадает с осью стержня.

Функция Q(x,t), описывающая продольные колебания стержня определяется уравнением:

.

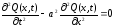Начальные условия нулевые:

;

.

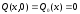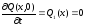Граничные условия задаются в виде:

;

,

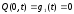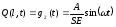где S – площадь поперечного сечения стержня, м²;

E – модуль Юнга материала стержня, Па (см. Приложение).

Общие замечания.

1) Если рассматривается колебательный процесс струны (стержня), у которой концы находятся достаточно далеко и в течение небольшого интервала времени влияние концов еще не успевает проявиться, то можно считать струну бесконечной. При этом рассматривается задача, в которой -∞<x<∞ и граничные условия не формулируются.

2) Если рассматриваемый участок струны (стержня) находится вблизи от одного его конца и далеко от другого, то рассматривается задача о полубесконечной струне, когда 0≤x<+∞ и граничные условия формулируются только на одно ее конце.

2.3 Уравнения крутильных колебаний стержня

Рассмотрим круговой цилиндрический стержень длиной l, который под влиянием некоторой причины совершает крутильные колебания. Под крутильными колебаниями будем понимать такие колебания, когда поперечные сечения стержня остаются плоскими и поворачиваются одно относительно другого без искажений, вращаясь вокруг оси стрежня.

Тогда уравнение, описывающее крутильное колебание стержня имеет вид:

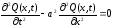, (2.26)

где а – скорость, м/с, определяемая из выражения:

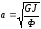, (2.27)

где G – модуль сдвига (описывает отклик материала на сдвиговую нагрузку), Па;

J – полярный момент инерции поперечного сечения, кг·м²;

Ф – осевой момент инерции стержня, приведенный к длине, кг·м.

Модуль сдвига связан с модулем Юнга Е через коэффициент Пуассона υ:

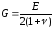. (2.28)

Значения модуля сдвига для ряда материалов при комнатной температуре представлены в таблице.

Таблица - Значения модуля сдвига G для ряда материалов

№	Материал	G, ГПа	№	Материал	G, ГПа
1	Алмаз	478	4	Алюминий	25,5
2	Сталь	79,3	5	Полиэтилен	0,117
3	Стекло	41,4	6	Резина	0,0006

Пример.

Пусть один конец круглого однородного вала закреплен (х=0), а к другому его концу (х=l) жестко прикреплен диск с моментом инерции J. В начальный момент времени диск закручивается на угол α и отпускается без начальной скорости. Поставить краевую задачу для определения углов поворота поперечных сечений вала при t>0.

Уравнение, описывающее данный процесс имеет вид:

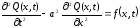, 0≤х≤l

где Q(x,t) – угол поворота сечения вала с координатой х в момент времени t;

f(x,t)=0;

,

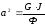где G – модуль сдвига, Па;

Ф – осевой момент инерции единицы длины вала, кг·м.

Начальные условия при этом имеют вид:

- профиль начальных смещений

;

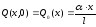- профиль начальной скорости:

.

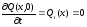Граничные условия задаются в виде:

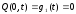- жесткое закрепление левого конца;

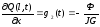- закрепление диска с моментом инерции J/

2.4 Уравнение колебаний мембраны

Рассмотрим мембрану (тонкую пленку, в которой возникает сопротивление деформациям изгиба и сдвига), расположенную в равновесном положении в плоскости хОу. Колебания точек мембраны в направлении, перпендикулярном плоскости хОу описываются функцией Q(x,у,t) согласно уравнению:

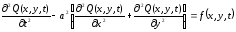, (2.29)

где а – волновая скорость мембраны, м/с;

f(x,у,t) – внешнее воздействие, м/с².

Далее может быть использовано обозначение оператора Лапласа, которое в декартовой системе координат имеет вид (см. Приложение):

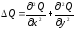. (2.30)

С учетом оператора Лапласа (2.30) уравнение (2.29) может быть представлено в виде:

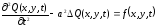(2.31)

Волновая скорость определяется согласно выражению:

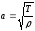, (2.32)

где Т – натяжение, приложенное к контуру единичной длины, Н/м;

ρ – поверхностная плотность (масса, приходящаяся на единицу длины площади мембраны), кг/м².

Внешнее воздействие f(x,у,t) может быть выражено через поверхностную плотность силы g(x,у,t), т.е. силу, действующую на единицу площади (Н/м²):

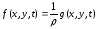. (2.33)

Аналогично колебанию струны, в случае отсутствия внешней силы f(x,у,t)=0, получаем уравнение свободных колебаний мембраны.

Начальные условия задаются в виде:

- профиля начальных смещений мембраны:

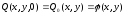; (2.34)

- профиля начальной скорости мембраны:

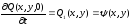. (2.35)

Граничные условия формулируются аналогично струне.

1) Так для мембраны, закрепленной на границе:

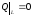при t≥0,

где L – граница мембраны.

Для квадратной мембраны (0≤х≤l₁) и (0≤у≤l₂) граничные условия запишутся в виде:

;

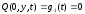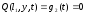; (2.36)

;

.

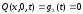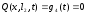2) Если края мембраны свободны, т.е. они могут свободно перемещаться по вертикальной боковой поверхности цилиндра с основанием L (в случае круглой мембраны), то граничные условия имеют вид:

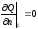. (2.37)

Для квадратной мембраны в этом случае условия принимают вид:

;

;

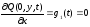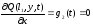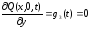; (2.38)

.

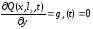3) Если края мембраны упруго закреплены, то:

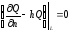, (2.39)

где h=k/T;

k – жесткость закрепления мембраны.

Описанная задача применительно к квадратной мембране. Рассмотрим случай круглой мембраны радиусом R с центром в начале координат. В этом случае удобно использовать полярные координаты r и φ. Тогда отклонение точек мембраны будет описываться функцией Q(r,φ,t), а уравнение иметь вид:

.

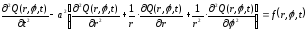Данное уравнение получено из (2.29) путем использования выражения для оператора Лапласа ΔQ в полярных координатах:

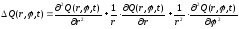. (2.40)

Для данной задачи начальные и условия запишутся в виде:

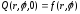; (2.41)

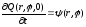. (2.42)

Граничное условие, например, в случае жесткого закрепления мембраны:

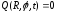. (2.43)

Если рассматривается задача об осесимметричных колебаниях мембраны, не зависящих от угла φ, уравнение упрощается и приобретает вид:

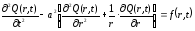. (2.44)

Начальные и граничные условия при этом:

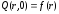; (2.45)

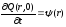; (2.46)

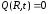. (2.47)

Пример 1.

Сформулировать краевую задачу о свободных колебаниях прямоугольной мембраны (0≤х≤l₁, 0≤y≤l₂), если в начальный момент времени t=0 отклонение точек мембраны от плоскости xOy описывается функцией xy(l₁-x)( l₂-y), а начальная скорость равна нулю. Вдоль контура мембрана закреплена неподвижно.

Функция Q(x,t), описывающая свободные колебания мембраны определяется уравнением:

.

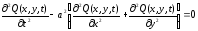Начальные условия описываются следующим образом:

;

.

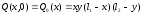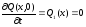Граничные условия задаются в виде:

; ;

; .

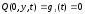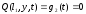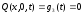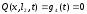Пример 2.

Круглая однородная мембрана радиуса R, закрепленная по контуру, находится в состоянии равновесия при натяжении Т₀. В момент времени t=0 к поверхности мембраны приложена равномерно распределенная гармоническая сила плотностью g(r,t)=Asin(ωt). Сформулировать краевую задачу при данных условиях.

Функция Q(r,t), описывающая колебания круглой мембраны определяется уравнением:

,

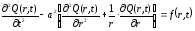где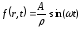

Начальные и граничные условия при этом:

; ;

.

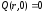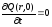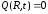2.5 Уравнение распределения температуры в стержне

Рассмотрим тонкий стержень, в пределах любого сечения которого температуру будем считать постоянной, окруженный теплоизолирующей оболочкой. Направим ось Ох вдоль данного стержня. Температура стержня в каждой его точке х в момент времени t описывается функцией Q(x,t) согласно уравнению:

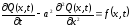, (2.48)

где а² – коэффициент температуропроводности, м²/с;

f(x,t) – внешнее воздействие, К/с.

Коэффициент температуропроводности рассчитывается из выражения:

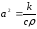, (2.49)

где k – коэффициент теплопроводности вещества, Вт/(м·К);

c – удельная теплоемкость вещества, Дж/(кг·К);

ρ – плотность вещества, кг/м³.

Внешнее воздействие определяется следующим образом:

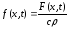, (2.50)

где F(x,t) – функция плотности тепловых источников, которая определяет количество теплоты, выделяющееся за единицу времени в единице объема тепла

Некоторые значения коэффициента температуропроводности представлены в таблице (Эдвардс,с838).

Таблица – Коэффициенты температуропроводности материалов

№	Материал	а2, м2/с
1	Серебро	1,7·10-4
2	Медь	1,15·10-4
3	Алюминий	0,85·10-4
4	Железо	0,15·10-4
5	Бетон	0,005·10-4

Начальные условия для уравнения теплопроводности состоят в задании температуры всех точек стержня в начальный момент времени:

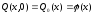. (2.51)

Для задания граничных (краевых условий) могут быть использованы следующие варианты: (Кузнецов,66)

1) Температура на конце стержня поддерживается по определенному закону (граничные условия первого рода):

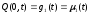; (2.52)

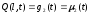. (2.53)

2) На конце стержня (например, при х=0) задан тепловой поток q(t) – граничные условия второго рода:

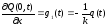, (2.54)

где k – коэффициент теплопроводности вещества, Вт/(м·К).

В частности в случае теплоизолированного конца тепловой поток через него отсутствует:

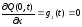. (2.55)

3) На конце стержня происходит теплообмен с окружающей средой по закону Ньютона – граничные условия третьего рода.

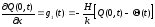, (2.56)

где Θ(t) – температура окружающей среды;

Н – коэффициент теплообмена, т.е. количество тепла, прошедшее через единичную площадку сечения стержня за единицу времени при изменении температуры на один градус, Вт/(К·м²).

Пример 1(Эдвардс,с838)

Пусть стержень длиной l погружают в пар до тех пор, пока температура во всех его точках не достигнет 100⁰С. В момент времени t=0 его боковую поверхность теплоизолируют, а его оба конца вставляют в лед при 0⁰С. Сформулировать краевую задачу для вычисления температуры стержня после выполнения сформулированных условий.

Функция Q(x,t), описывающая распределение температуры в стержне определяется уравнением:

,

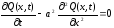где 0≤х≤l;

а² - коэффициент температуропроводности материала стержня.

Начальные условия:

Q(x,0)=100.

Граничные условия:

Q(0,t)=Q(l,t)=0.

Пример 2.

Поставить краевую задачу определения температурного поля одномерного однослойного шара радиусом R. В начальный момент времени температурное поле подчиняется закону F(r). Шар помещен в среду с температурой Θ, при этом теплообмен на поверхности подчиняется закону Ньютона и коэффициент теплоотдачи (теплообмена) равен Н. Коэффициент теплопроводности шара k.

Так как в задаче рассматривается одномерный шар, то это означает симметричное температурное поле по всем направлениям. Тогда можете быть использовано уравнение теплопроводности в полярных координатах, которое с учетом отсутствия внутренних источников тепла имеет вид:

,

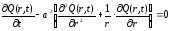Начальные условия при этом определяются заданным законом:

;

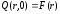Граничные условия на поверхности шара запишем как гранияные условия третьего рода:

,

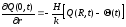Шар имеет центральную точечную симметрию. При равномерном теплообмене по поверхности температурное поле будет симметричным. В связи с этим появляются дополнительное условие симметрии:

.
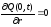