курсовая работа / Оптимизация факторного процесса

МИНИСТЕРСТВО РФ ПО ВЫСШЕМУ И ПРОФЕССИОНАЛЬНОМУ

ОБРАЗОВАНИЮ

САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ

КАФЕДРА УИТ

КУРСОВАЯ РАБОТА

По курсу: “Моделирование систем управления”

Тема: “Оптимизация факторного процесса”

Выполнил: ст. гр. УИТ-42

Сысолятин А. С.

Принял: преп. каф.

Фролова М. А.

Балаково 1999

Задание 1. Вариант 21.

Оптимизация вибрационного расходомера.

Таблица 1

Факторы	-1	1
x1 Диаметр трубки мм	4	6
x2 Диаметр кольца мм	160	190
x3 Угол при колебании кольца вокруг оси градус	0	0,5
x4 Частота колебаний кольца Гц	9,95	10,05

Составить 2^4-1.

Проведем оптимизацию дробнофакторного эксперимента.

Так как задача допускает выбор параметра оптимизации, каждый из факторов предполагается управляемым, опыты равноценны и воспроизводимы воспользуемся методом Бокса – Уилсона. Будем рассматривать задачу с максимальным числом факторов равным четырем и числом опытов 2^4-1=8.

Составим матрицу планирования для линейной модели в первом приближении. В качестве нового фактора берем столбец с максимальным разрешением

Таблица №2

№	х0	х1	х2	х3	х1*х3*х2	У1	У2	У3	уср	S2	ŷ	у2
1	+	-	-	-	-	16,25	16,35	20	16,3	0,005	15,625	0,45563
2	+	+	-	-	+	15,7	15,81		15,755	0,00605	15,7925	0,00141
3	+	-	+	-	+	12,12	12,25		12,185	0,00845	12,8	0,37822
4	+	+	+	-	-	15,75	15,87		15,81	0,0072	15,8325	0,00051
5	+	-	-	+	+	16,2	16,35		16,275	0,01125	16,2975	0,00051
6	+	+	-	+	-	18,75	18,68		18,715	0,00245	19,33	0,37822
7	+	-	+	+	-	16,35	16,25		16,3	0,005	16,3375	0,00141
8	+	+	+	+	+	17,24	17,12		17,18	0,0072	16,505	0,45563

Подсчитываем средние значения в сериях .

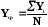(1)

где у_i – i-ое значение в серии опытов;

N – количество опытов в серии.

Подсчитываем дисперсию S² различных серий опытов.

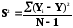(2)

Проверяем первую серию опытов на наличие ошибки.

Так как дисперсия S²=0,005, то

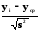=52,32>t=12,71 (3)

где t – коэффициент Стьюдента для степени свободы

(n – 1)=(2 – 1)=1.

t=12.71

А, значит значение опыта равное 11 – промах и из дальнейшего рассмотрения мы его исключаем.

Проверяем дисперсию на однородность.

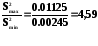(4)

Полученное значение меньше табличного значения критерия Фишера равного F=164 для степеней свободы числителя f₁ = n-1=1 и знаменателя

f₁ = n – 1=1.

Находим дисперсию выходного параметра.

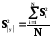=0,00658

Записываем линейную модель:

у=b₀+b₁х₁+b₂х₂+ b₃х₃ +b₄х_1*х_2*х₃

Получили следующие значения коэффициентов

b0=	16,065
b1=	0,8
b2=	-0,696
b3=	1,0525
b4=	-0,7163

Линейная модель запишется в виде:

ŷ=16,065+0,8х₁-0,696х₂+1,0525х₃-0,7163x₅

Рассчитываем по этой модели расчетные значения параметра оптимизации

ŷ= f(x) и заносим эти значения в таблицу.

После чего находим квадрат отклонения расчетного значения от экспериментального

у² =(ŷ – у_ср)²

и заносим полученные значения в таблицу.

Затем находим дисперсию адекватности для равномерного дубирования

S²_АД = 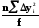=1,1144

где: f=N- (k+1)=8-5=3

Проверяем модель на адекватность, для чего находим расчетный коэффициент Фишера как отношение:

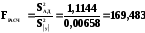
Полученное значение сравниваем с табличным значением критерия Фишера F = 6,6 f₁=n-1=2-1=1; f₂=N-(n+1)=8-(2+1)=5 и поскольку полученное значение превышает его, то полученная линейная модель неадекватна.

Оценим значимость коэффициентов для чего найдем дисперсию коэффициентов регрессии:

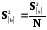== 0,00082

Определим доверительный интервал

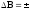t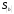=12,71*0,02863=0,36437

Так как все коэффициенты по абсолютной величине больше доверительного интервала, то все они значимы.

Приступим к нахождению максимального значения параметра оптимизации движением по градиенту.

Основной уровень выбираем как центр области, так как не известно никакой дополнительной информации о лучших точках.

Найдем произведение I_j*b_j для каждого фактора. Далее, определяем шаги движения по факторам. Методом подбора были определены наиболее оптимальные шаги для каждого фактора, полученные путем деления вышеуказанного произведения на (7,25).

И, наконец, находим значение параметра оптимизации, предварительно переведя натуральные значения факторов в кодированные согласно формуле:

х_i=(X_i – X_{i o})/I_j

Таблица №3

Натуральные значения	X1	X2	X3	X4	Y
Основной уровень	5	175	0,25	10
Ji–интервал варьирования	1	15	0,25	0,05
Верхний уровень	6	190	0,5	10,05
Нижний уровень	4	160	0	9,95
Кодированное значение	x1	x2	x3	x1*x2*x3	Уср
Опыты 1	-	-	-	-	15,625
2	+	-	-	+	15,7925
3	-	+	-	+	12,8
4	+	+	-	-	15,8325
5	-	-	+	+	16,2975
6	+	-	+	-	19,33
7	-	+	+	-	16,3375
8	+	+	+	+	16,505
bJ= 16,065	0,8	-0,696	1,0525	-0,7163
bJ*JJ	0,8	-10,444	0,263125	-0,0358
шаг	0,11034	-1,44052	0,03629	-0,0049
опыт 1	5,11034	173,559	0,28629	9,99506
2	5,22069	172,119	0,32259	9,990121
3	5,33103	170,678	0,35888	9,985181
4	5,44138	169,238	0,39517	9,980241
5	5,55172	167,797	0,43147	9,975302
6	5,66207	166,357	0,46776	9,970362
7	5,77241	164,916	0,50405	9,965422
8	5,88276	163,476	0,54034	9,960483
9	5,9931	162,035	0,57664	9,955543
кодированные значения	x1	x2	x3	x1*x2*x3	ŷ
опыт 1	0,11034	-0,096	0,14517	-0,098793	16,4437
2	0,22069	-0,1921	0,29034	-0,197586	16,8224
3	0,33103	-0,2881	0,43552	-0,296379	17,2011
4	0,44138	-0,3841	0,58069	-0,395172	17,5798
5	0,55172	-0,4802	0,72586	-0,493966	17,9585
6	0,66207	-0,5762	0,87103	-0,592759	18,3372
7	0,77241	-0,6722	1,01621	-0,691552	18,7159
8	0,88276	-0,7683	1,16138	-0,790345	19,0946
9	0,9931	-0,8643	1,30655	-0,889138	19,4732

Максимальное значение параметра оптимизации 19,47 оно достигается при X1=5,99: X2=162.035; X3=0.576; X4=9.9555