- 32

Введение

Под моделированием понимается процесс замещения реального объекта некоторой моделью, позволяющей проводить над ней определённые исследования. В зависимости от уровня абстрагирования выделяют три иерархических уровня: микро-, макро- и мегауровень. Цель курсовой работы – моделирование некоторых физических процессов на микро- и макроуровнях.

Под моделированием на микроуровне понимается также теория систем с распределёнными параметрами. Есть среды, которые не могут быть описаны в сосредоточенных параметрах (электромагнитное поле, электростатическое поле, течение потока, гравитационное поле, температура и т.д.). Система с распределенными параметрами (СРП) - это система, в которой практически все сигналы (особенно входной и выходной) зависят от пространственных координат и времени. Система с сосредоточенными параметрами является частным случаем СРП и вводится для упрощения и решения задач на первом (нулевом) этапе. Математически СРП описываются дифференциальными уравнениями в частных производных с начальными и граничными условиями, составляющими краевую задачу. Для её решения в статике и динамике используется функция Грина, являющаяся решением краевой задачи при воздействии на неё дельта-функции и нулевых начальных и граничных условиях, а также континуальная передаточная функция, являющаяся преобразованной по Лапласу функцией Грина. В данной работе при моделировании на микроуровне решается вопрос построения математической модели диска, закрепленного по краям.

На макроуровне исследуется гидравлическая система. При разработке и исследовании модели макроуровня необходимо выполнить: синтез моделей в графической и матричной формах, в виде системы обыкновенных дифференциальных уравнений, а также анализ полученной математической модели в статическом и динамическом режимах.

1 МОДЕЛИРОВАНИЕ НА МИКРОУРОВНЕ

1.1 Исходные данные

Есть среды, которые не могут быть описаны в сосредоточенных параметрах (электромагнитное поле, электростатическое поле, течение потока, гравитационное поле, температура и так далее), поэтому они рассматриваются как системы с распределёнными параметрами (СРП).

Конечной задачей решения уравнения СРП является нахождения выходной распределённой величины Q(x,t) в любой момент времени t>0 в любой пространственной точке х.

Рассмотрим одномерную задачу — колебание струны, которое может быть описано уравнением гиперболического типа:

где f(x,t) - входная координата, зависящая от координаты х и времени t, для которого формируются следующие условия:

1) Начальные условия:

2) Граничные условия:

, ,

Стандартизирующая функция, компенсирующая влияние начальных и граничных условий для данной задачи имеет вид:

Функция Грина, являющаяся решением краевой задачи при нулевых граничных условиях и входном воздействии в виде δ-функции имеет вид:

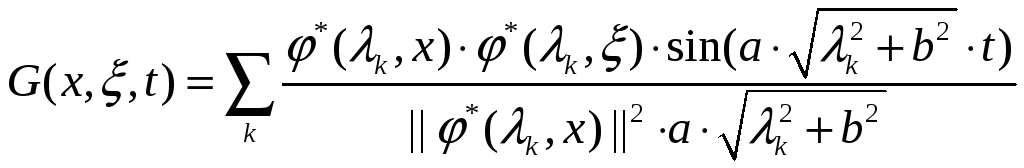
Континуальная передаточная функция, являющаяся преобразованием Лапласа функции Грина имеет вид:

где λ_к – положительные корни следующего уравнения:

1.2 Идентификация краевой задачи

Для решения частной задачи примем следующие условия:

– входное возмущение

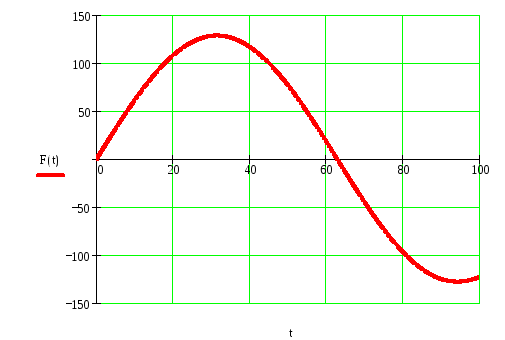
Рисунок 1 – Входное возмущение

– начальные условия, описывающие положение струны в начальный момент времени ,

– граничные условия, описывающие колебание струны на концах стержня

,

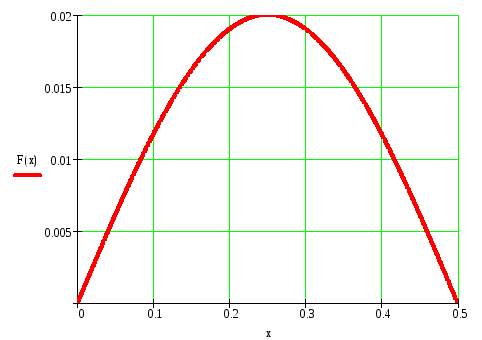
Рисунок 2 – Начальные условия

Найдем корни уравнения графически.

Примем , ,

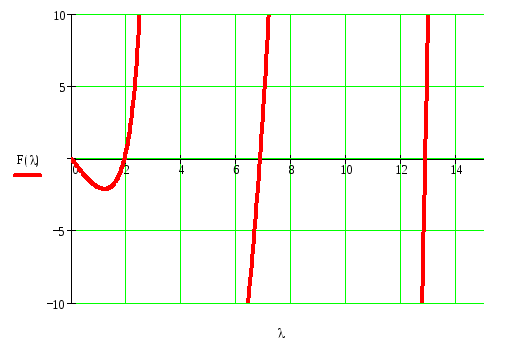
Рисунок 3 – График функции

Рассчитаем размерность для f(x,t):

,

где p – давление на струну, [Н/м²];

ρ – плотность материала струны, [кг/м³];

– длина струны, [м].

Тогда:

.

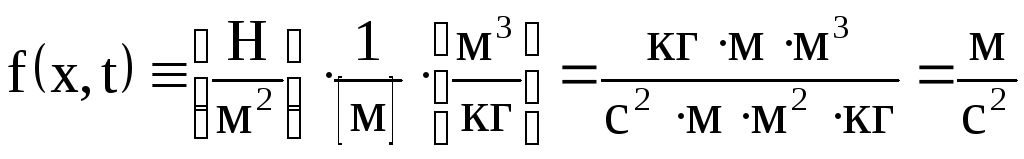Рассчитаем размерность для а:

,

где T – натяжение струны, [Н/м²];

ρ – плотность материала струны, [кг/м³].

Тогда:

.

Примем, что:

– а = 10 – волновая скорость струны;

– l = 0,5 [м] – длина струны;

– материал струны – сталь;

– ρ = 7.8 · 10³ – плотность стали.

С учётом входного воздействия, принятых начальных и граничных условий стандартизирующая функция примет вид:

где – импульсная переменная функция.