БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ ТЕХНОЛОГИИ И УПРАВЛЕНИЯ

ФАКУЛЬТЕТ “ИНЖЕНЕРНО-СТРОИТЕЛЬНЫЙ”

Курсовая работа

по курсам «Моделирование систем управления»

на тему «Моделирование динамической системы методом планирования эксперимента»

Выполнил: ст. гр. УИТ-42

Проверила:

2001

Содержание

Введение. 2

Исходные данные 3

Построение матрицы планирования 3

Расчет линейной модели 6

Оценка адекватности модели 6

Расчет крутого восхождения 7

Введение.

Цель работы – изучение метода планирования эксперимента при исследовании многофакторной динамической системы и его применения для получения линейной математической модели и проверки ее адекватности.

Построение моделей по результатам наблюдений представляет собой формализацию, необходимую для определения основных признаков, связей и закономерностей, присущих объекту, и отсеивания второстепенных признаков. В качестве динамических объектов могут рассматриваться технические системы и процессы в них. Для одного и того же объекта в зависимости от конкретных требований практики и типа решаемой задачи может быть построен ряд моделей различной сложности.

В данной курсовой работе решается вопрос построения моделей на основе экспериментальных данных.

Идентификация динамических объектов (систем или процессов) сводится к задаче построения математической модели, адекватной исследуемому объекту. Для получения математической модели необходимо построить идеализированную модель объекта на основе изучения физических процессов в нем и уточнить значение параметров модели на основе результатов специальных экспериментов. Для идентификации динамических объектов может быть использован метод планирования эксперимента (МПЭ). Под планированием эксперимента понимают процесс определения числа и условий проведения опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью. Эффективность использования МПЭ при исследовании процессов в различных объектах объясняется тем, что их наиболее важные характеристики являются случайными величинами, распределение которых близко к нормальному.

Основная задача исследований – оптимизация, заключающаяся в нахождении совокупности варьируемых параметров, при которых выбранная целевая функция (параметр оптимизации) принимает экстремальное значение.

Исходные данные

Вариант 7-12. Составить план 2^4-1

Уровни факторов	Факторы процесса
	X1	X2	X3	X4
Нижний	6	70	0.22	12
Основной	8	75	0.36	32
Верхний	10	80	0.50	52

Массив данных В9

Y1	Y2	Y3
0.12	0.91	0.13
0.06	0.06	0.08
0.20	0.21	0.20
0.18	0.18	0.17
0.12	0.14	0.16
0.12	0.11	0.10
0.23	0.22	0.21
0.21	0.20	0.18

Построение матрицы планирования

Определим интервал варьирования по выражению:

. (1)

Таблица №1

Уровни факторов и интервалы варьирования

Уровни факторов	Факторы процесса
	X1	X2	X3	X4
Нижний	6	70	0.22	12
Основной	8	75	0.36	32
Верхний	10	80	0.50	52
Интервал варьирования	2	5	0.14	20

Таблица №2

Матрица планирования дробного факторного эксперимента

Номер точки плана	Факторы				Значение параметра оптимизации
	X1	X2	X3	X4	Y
1	-	-	-	-	Y1
2	+	-	-	-	Y2
3	-	+	-	-	Y3
4	+	+	-	-	Y4
5	-	-	+	-	Y5
6	+	-	+	-	Y6
7	-	+	+	-	Y7
8	+	+	+	-	Y8
9	-	-	-	+	Y9
10	+	-	-	+	Y10
11	-	+	-	+	Y11
12	+	+	-	+	Y12
13	-	-	+	+	Y13
14	+	-	+	+	Y14
15	-	+	+	+	Y15
16	+	+	+	+	Y16

Таблица №3

Экспериментальные данные

№ опыта	Y1	Y2	Y3	Y4
1	0,12	1,1	0,11	0,12
2	0,06	0,06	0,06	0,08
3	0,2	0,18	0,22	0,2
4	0,18	0,16	0,18	0,16
5	0,14	0,12	0,14	0,16
6	0,11	0,12	0,1	0,1
7	0,24	0,23	0,24	0,21
8	0,12	0,11	0,1	0,13
9	0,04	0,06	0,08	0,08
10	0,18	0,18	0,2	0,21
11	0,18	0,14	0,18	0,17
12	0,13	0,14	0,14	0,17
13	0,11	0,12	0,11	0,1
14	0,26	0,25	0,23	0,2
15	0,22	0,23	0,21	0,17
16	0,2	0,22	0,2	0,18

Определим ошибки опыта по следующим показателям:

1. Среднее арифметическое результатов:

= (y₁ + y₂ + y₃ + . . . + y_n) / n = (2)

где у_l - результаты экспериментов, n - количество опытов в серии.

n = 4;

2. Дисперсия - среднее значение квадрата отклонений величины от ее среднего значения:

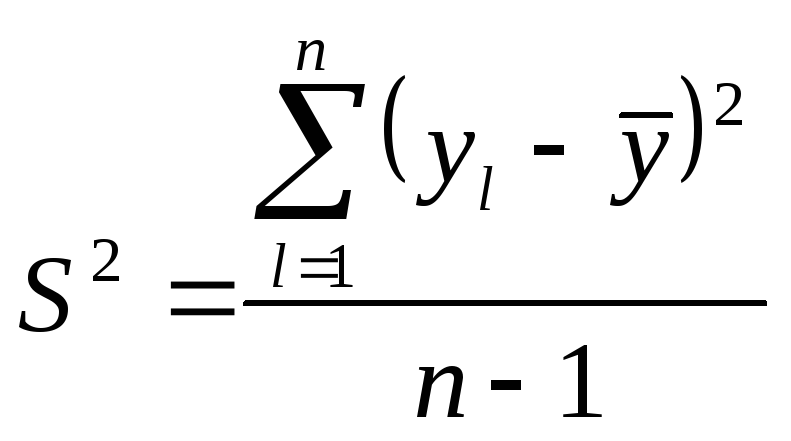, (3)

где (n-1) - число степеней свободы, равное количеству параллельных опытов минус единица.

3. Квадратичная ошибка или стандарт:

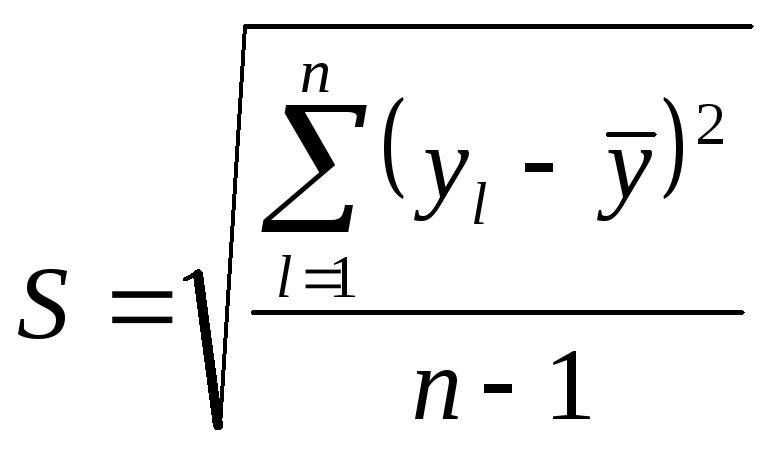. (4)

Результаты вычислений сведем в таблицу №4.

Таблица №4

№ опыта		S2	S	y2
1	0,116667	3,33333E-05	0,005774	0,000153657
2	0,065	0,0001	0,01	0,001477441
3	0,2	0,000266667	0,01633	0,002053223
4	0,17	0,000133333	0,011547	0,000260688
5	0,14	0,000266667	0,01633	6,10352E-05
6	0,1075	9,16667E-05	0,009574	0,000569021
7	0,23	0,0002	0,014142	0,002246365
8	0,115	0,000166667	0,01291	0,004458344
9	0,065	0,000366667	0,019149	0,003789941
10	0,1925	0,000225	0,015	0,004458344
11	0,1675	0,000358333	0,01893	8,98546E-05
12	0,145	0,0003	0,017321	0,000970063
13	0,11	6,66667E-05	0,008165	0,001978396
14	0,235	0,0007	0,026458	0,0066185
15	0,2075	0,000691667	0,0263	6,78168E-06
16	0,2	0,000266667	0,01633	1,65039E-05

Проверяем первую серию опытов на наличие ошибки.

Для определения ошибок опыта используем критерий Стьюдента:

;

S = 0.0057

=170t=3.18,

где t - коэффициент Стьюдента для степеней свободы (n-1)=3

А значит значение опыта равное 1.1 - промах и из дальнейшего рассмотрения мы его исключаем.

Проверяем дисперсию на однородность:

=0,0007/0.000033=21.21

f₁ = (n-1) = 3; (для опыта №14)

f₂ = (n-1) = 2. (для опыта №1)

Полученное значение больше табличного значения критерия Фишера равного F=19.2, значит дисперсии неоднородны.

Находим дисперсию выходного параметра или параметра оптимизации:

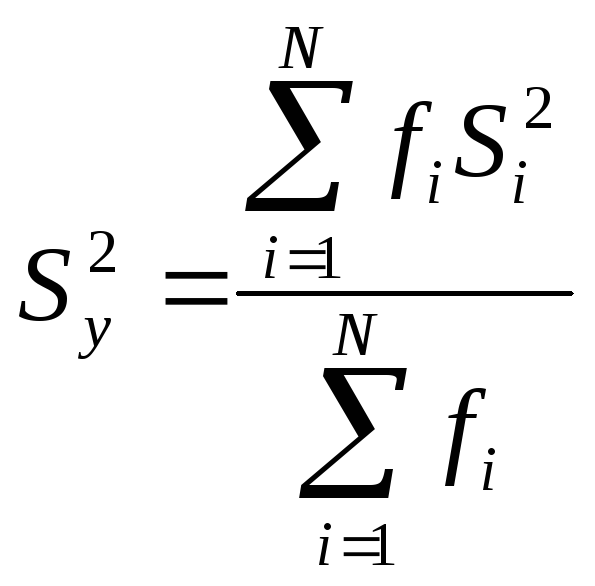= 0,000269504

где =15*3+2=47.