1.6 Моделирование в программе Elcut

При воздействии на диск в центр температурой Т=0К, модель будет иметь вид:

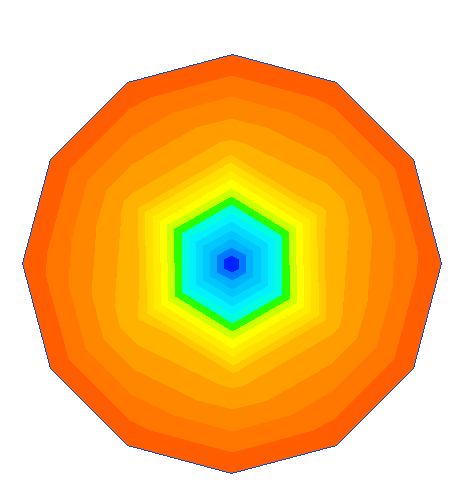
Рисунок 6 - Диск, при воздействии на него Т=0К

График изменения температуры по вдоль диаметра имеет вид:

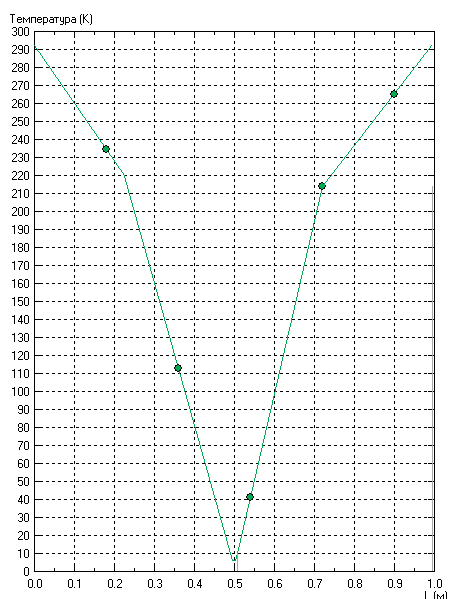
Рисунок 7 – График изменения температуры

С помощью прикладной программы Elcut мы имеем возможность определить различные показатели в произвольной точке.

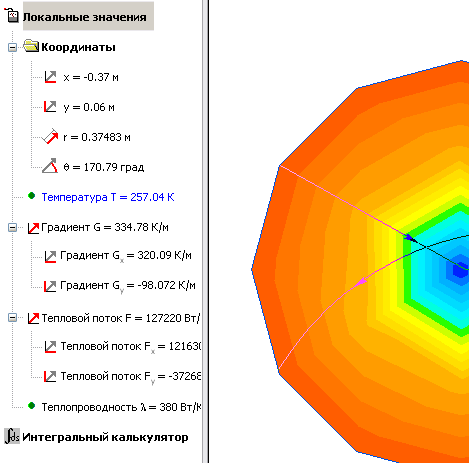
Рисунок 8 – Различные показатели в произвольной точке.

2. Моделирование на макроуровне

2.1 Исходные данные

Дана схема гидравлической системы, представленная на рисунке 11. В системе используется в качестве рабочей жидкости веретенное масло АУ. Материал трубопровода – сталь. Основные параметры системы и жидкости приведены в таблице 1 Параметры трубопроводов приведены в таблице 2

Рисунок 9– Схема гидравлической системы

Таблица 1 – Параметры системы и жидкости

Основные параметры	Обозначение	Значение
Плотность рабочей жидкости, кг/м3	ρ	860
Вязкость, м2/с	ν	0.15×10-4
Модуль упругости системы, Па	Eс	1.7×108
Модуль упругости трубопровода, Па	Eтр	2.1×1011
Коэффициент потерь на трение при турбулентном потоке	λт	0.03
Толщина стенки трубопровода, м	δтр	2.2×10-3

Таблица 2 – Параметры трубопроводов

Параметр	Обозначение	Номер трубопровода
		1	2	3	4	5
Диаметр трубопровода, м	dтр	1	2	3	4	1
Длина трубопровода, м	l	25	30	30	32	25
Коэффициент местных сопротивлений	ζ	1,5	2,5	2	0,9	1,5
Давление потребителей и насосов, МПа	p	4	5,5	5	3	4

2.2 Графические формы математической модели гидросистемы

На основании исходной принципиальной схемы гидравлической системы (рисунок 11) строится динамическая модель. Участки магистралей представляются как последовательное соединение инерционного и диссипативного элемента, причем для инерционного элемента указывается направление движения рабочей жидкости. В точки ветвления магистралей устанавливают упругие элементы, учитывающие сжимаемость жидкости и деформируемость стенок трубопровода. На рисунке 12 представлена полученная динамическая модель.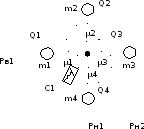

Рисунок 10 – Динамическая модель гидравлической системы.

2.3 Матричная форма математической модели

Для формирования полной математической модели на основе компонентных и топологических уравнений широкое применение получил узловой метод, для него необходимо сформировать матрицу инциденций, отражающую структуру связей всех элементов графа. Число строк матрицы соответствует числу узлов орграфа, число столбцов – числу ветвей. Отсутствие связи между узлом и ветвью обозначается «0», если ветвь входит в узел – «1», если выходит – «-1».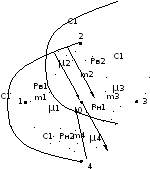

Рисунок 11– Ориентированный граф гидравлической системы

Таблица 3 – Матрица инциденций гидравлической системы

Узлы	Ветви
	Диссипативные				Упругие	Ветви внешнего воздействия
	μ1	μ2	μ3	μ4	С1	PB1	PB2	PH1	PH2
1	-1	0	0	0	+1	-1	0	0	0
2	0	-1	0	0	+1	0	-1	0	0
3	0	0	-1	0	-1	0	0	+1	0
4	0	0	0	-1	-1	0	0	0	+1