курсовая работа / курсвариант2
.docЗадание
1. Идентифицировать вид ДУ
-
По полученной выходной функции построить графики зависимостей выходной функции от точки приложения сигнала и от времени.
-
Синтезировать интегральную передаточную функцию
-
Построить ЛАЧХ и ФЧХ
-
Аппроксимировать ЛАЧХ
-
Получить выражение для оценочной интегральной передаточной функции
-
Сделать выводы.
Исходные данные.
Дифференциальное уравнение:
![]()
Начальные условия:
Q(x,0)=Q0(x), ,
![]() ;
;
Граничные условия:
Q(1,t)=g1(t), Q(l,t)=g2(t)
1 x l t0
Нормирующая функция задана в виде:
![]()
Функция Грина имеет вид:
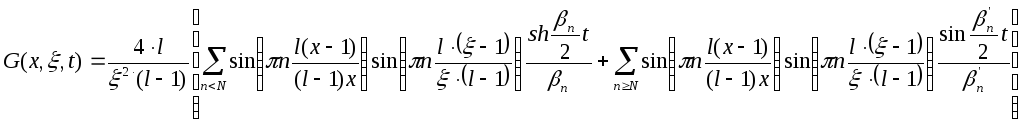 N-такое число, что
N-такое число, что
![]() 0 при nN,
0 при nN,
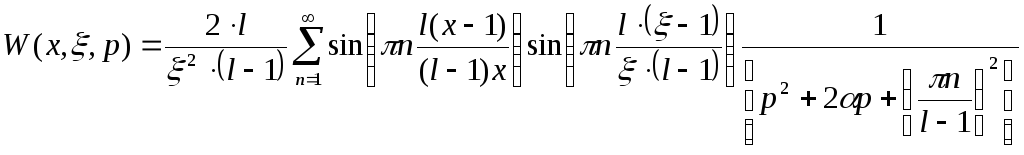
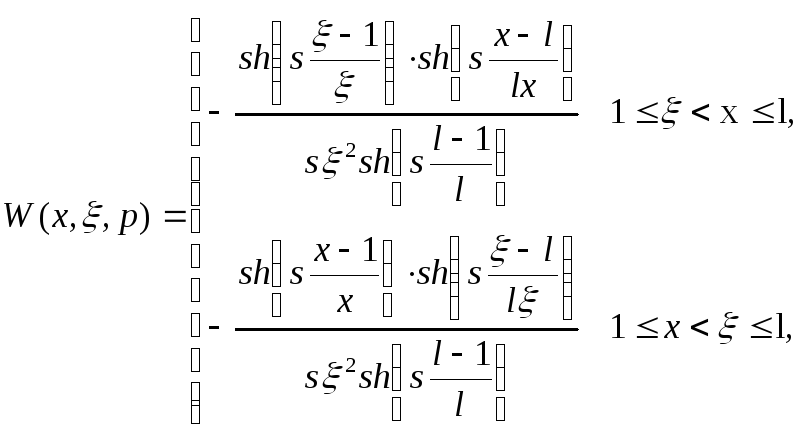
![]()
Введение
Система с распределёнными параметрами (СРП) – это система, в которой практически все сигналы (особенно входной и выходной) зависят от пространственных координат и времени.
Есть среды, которые не могут быть описаны в сосредоточенных параметрах (электромагнитное поле, течение потока, гравитационное поле, температура и т. д.).
Система с сосредоточенными параметрами является частным случаем СРП и выводится для упрощения и решения задач на первом (нулевом) этапе.
Практически все природные явления и функции могут быть описаны семью дифференциальными уравнениями в частных производных.
В данной курсовой работе решается вопрос построения математической модели элемента на основе теории распределённых сигналов.
Цель работы – синтез интегральной передаточной функции для объектов управления с распределёнными параметрами.
Решение.
По виду уравнения определяем, что рассматриваемый процесс можно идентифицировать, как продольные колебания стержня, концы которого движутся по заданному закону:
Пусть начальные условия и граничные нулевые:
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
Тогда нормирующая функция будет иметь вид:
![]()
Зная функцию Грина и нормирующую функцию можно найти выходную функцию по следующему выражению:
![]()
![]()
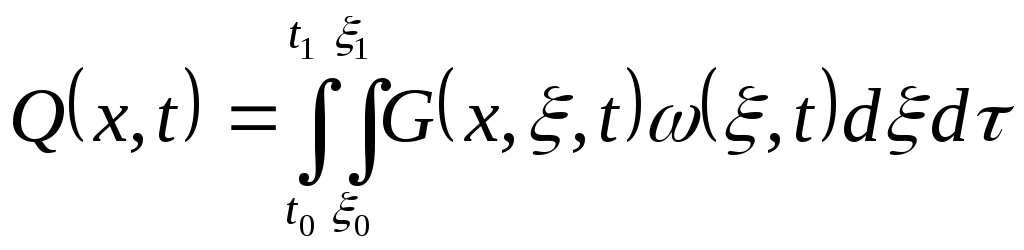
![]()
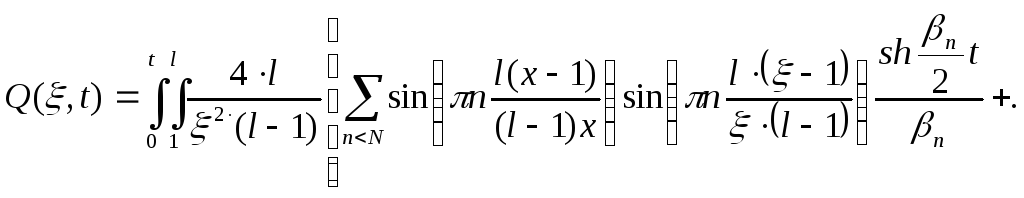
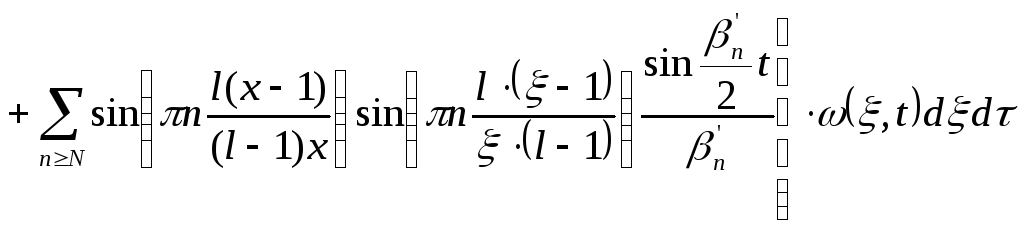
Пусть
![]() ,
l=2.65, тогда
,
l=2.65, тогда
![]() 0 при n2
.
0 при n2
.
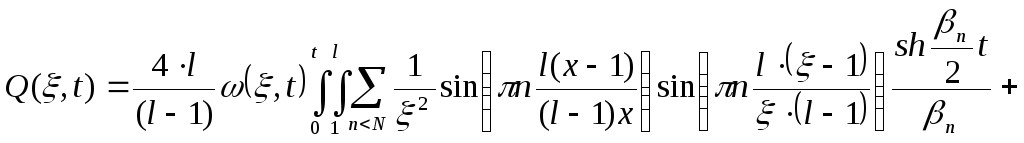
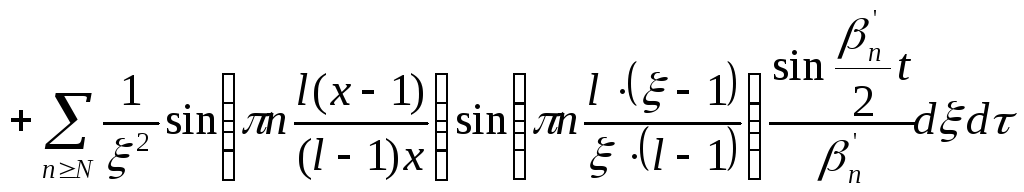
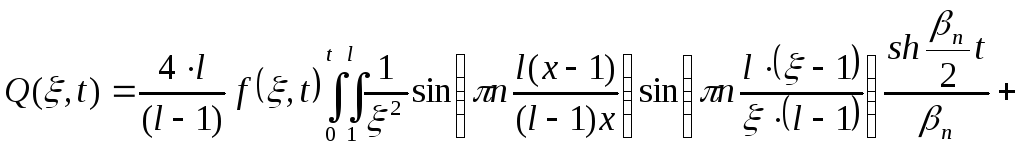
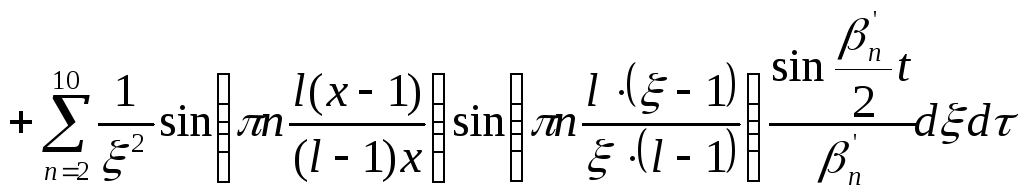
![]()
Разобьем полученный интеграл на 2части:
1)
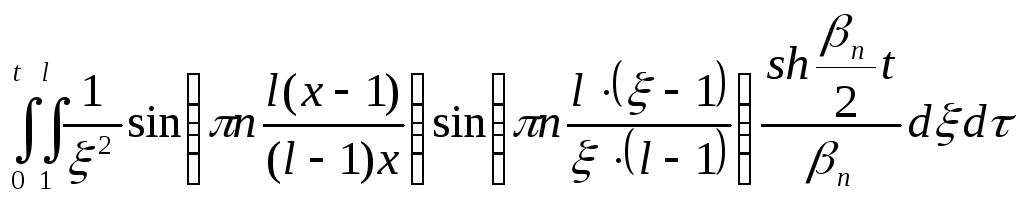 =
=
![]()
![]()
=![]() =
=![]() =
=
![]()
=![]()
![]() 2)
2)
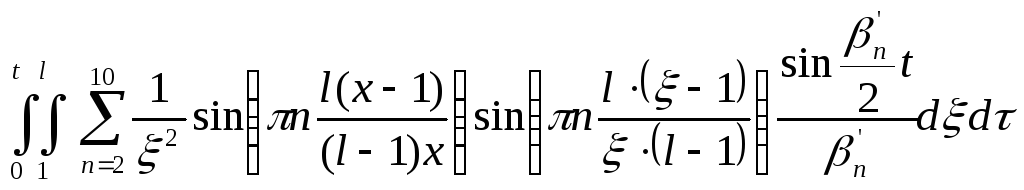 =
=
=![]()
+![]()
![]() )
)![]()
Разобьем полученный интеграл на несколько и посчитаем их по очереди:
![]() =
=
=
![]() =
=
=
![]()
![]()
![]()
![]() =
=![]()
![]() =
=
=
![]()
![]()
Сложим полученные выражения, тогда выходная функция запишется в виде:
![]()
![]() +
+
+
![]() +
+![]() +
+
+
+![]()
В результате вычислений, мы получили уравнение, описывающее зависимость выходной величины Q(x,t) от времени и координаты х в точке приложения входного воздействия.
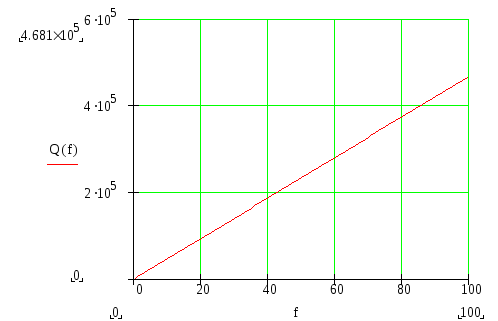
Построим статическую характеристику системы, которая описывается данным уравнением.
Введем следующие величины:
t=1c
x=1.5-точка воздействия
После подстановки данных получим:
![]()
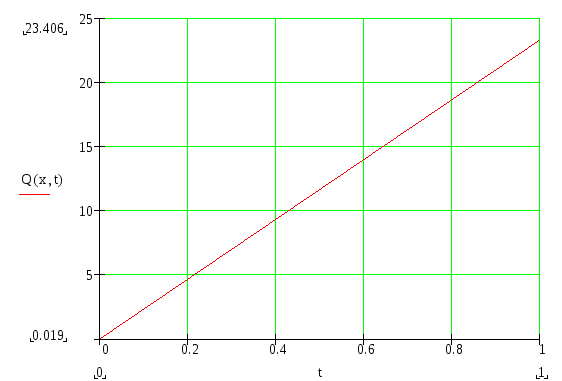
Построим
динамическую характеристику для системы,
описываемой уравнением Q(x,t)
при входном воздействии g=0.005,
остальные параметры остаются неизменными
t![]() .
.
Используя
выражение для континуальной передаточной
функции
![]() ,
построим следующие характеристики:
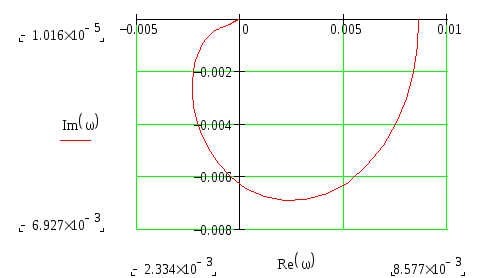
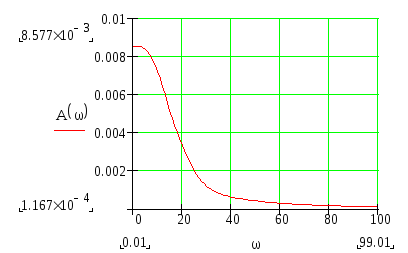
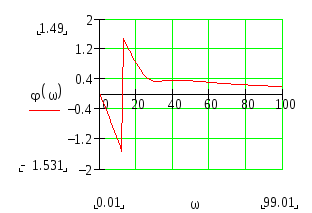
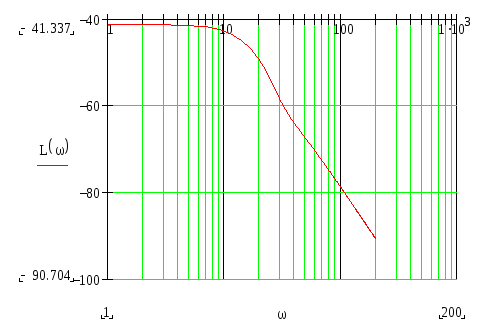
АФХ, АЧХ, ФЧХ и ЛАЧХ.
,
построим следующие характеристики:
АФХ, АЧХ, ФЧХ и ЛАЧХ.
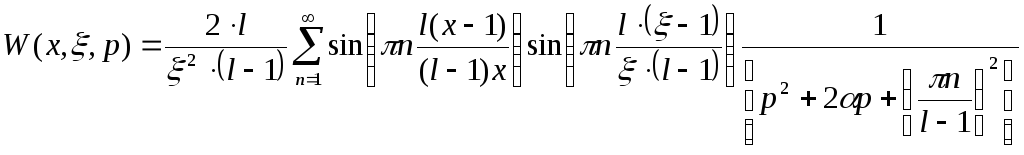
Заменяем
р на
![]()
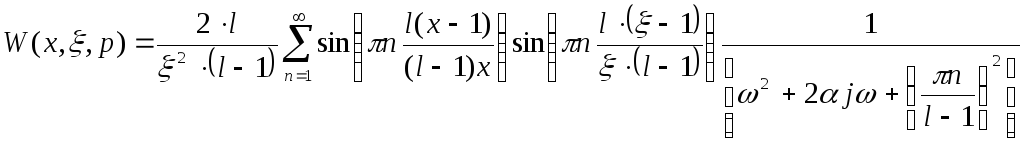
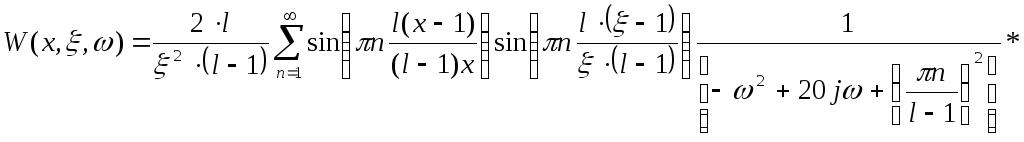
*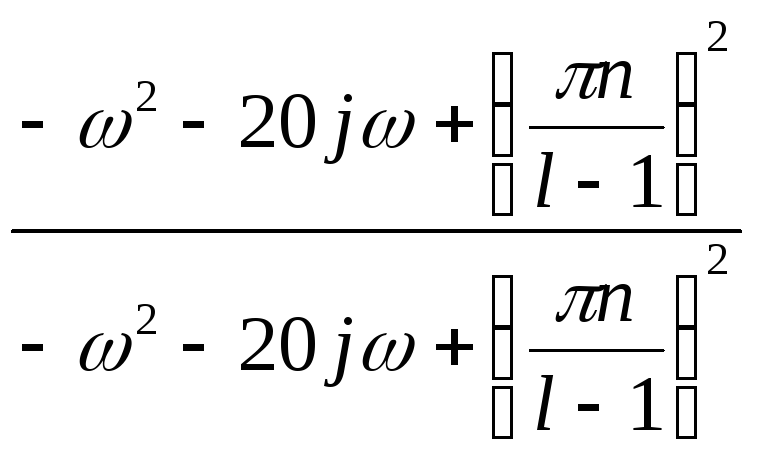 =
=
=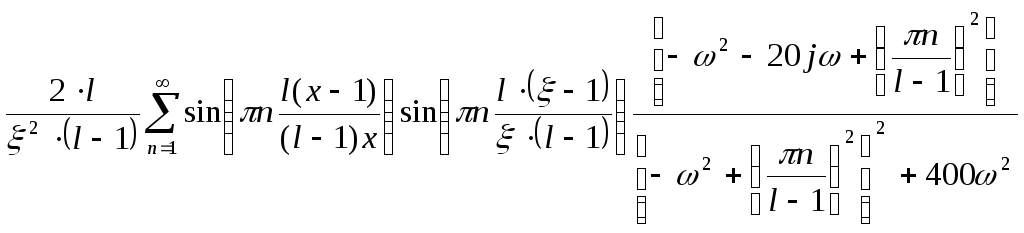 =
=
=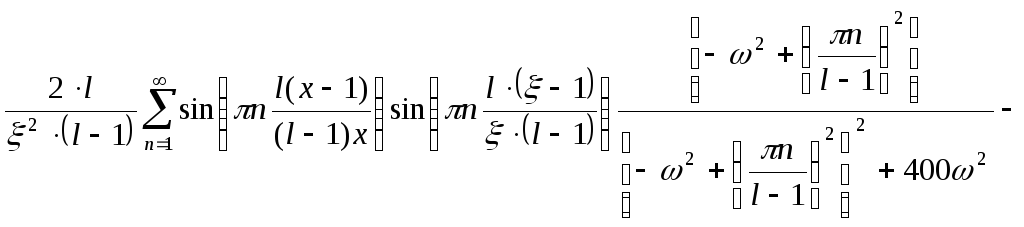
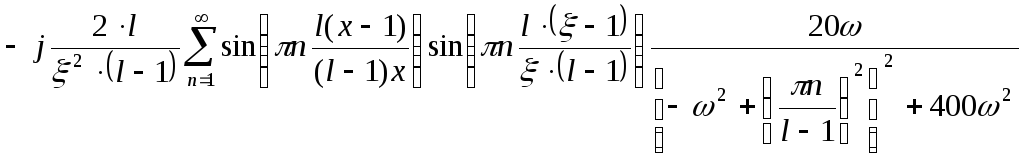
Представим континуальную передаточную функцию в следующем виде:
![]()
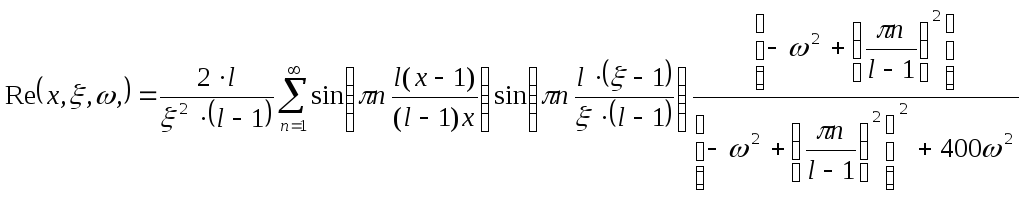
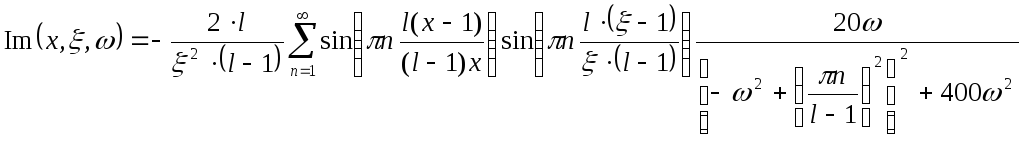
Построим графики АФХ, АЧХ, ФЧХ и ЛАЧХ