Содержание

Введение 3

СОДЕРЖАНИЕ 1

1 МОДЕЛИРОВАНИЕ НА МИКРОУРОВНЕ 3

1.1Постановка краевой задачи 3

1.2Расчёт выходной распределенной величины 5

1.3Оценка динамических свойств объекта моделирования 10

2 МОДЕЛИРОВАНИЕ НА МАКРОУРОВНЕ 15

2.1 Исходные данные 15

2.2 Графические формы математической модели гидросистемы 16

2.3 Матричная форма математической модели 17

2.4 Узловой метод формирования математической модели 19

2.5 Расчет параметров трубопровода гидросистемы 19

2.6 Расчет статического режима работы гидросистемы 21

2.7 Анализ динамических свойств гидросистемы 24

ЗАКЛЮЧЕНИЕ 29

1 Моделирование на микроуровне

1. Постановка краевой задачи

Сформулировать и решить краевую задачу о колебаниях однородной мембраны (0<r<R), закрепленной по контуру, под действием внешней непрерывно распределенной силы с плотностью g(r,t)=Asin(ωt). Начальное отклонение задать самостоятельно, а начальную скорость принять равной нулевой.

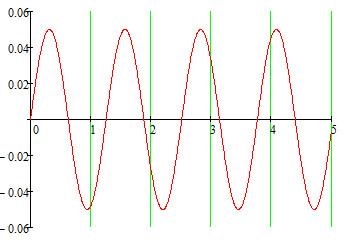
Колебания струны осуществляется под действием внешней непрерывно распределенной силы с плотностью g(r,t)=0.05∙sin(5t) Н/м, график которой представлен на рисунке 1.1.

Рисунок 1.1 – Плотность внешней силы

Материал мембраны - резина, радиусR=0.5 м.

Сформулируем краевую задачу для данного условия.

Функция Q(r,t), описывающая поперечные смещения струны определяется уравнением:

. (1)

Данное уравнение одномерное гиперболического типа (содержащее вторые производные по времени t и пространственной координате r).

Опишем параметры, входящие в данное уравнение.

Волновая скорость струны определяется выражением:

, (2)

где Т₀ – сила натяжения струны, Н;

ρ_П – поверхностная плотность (масса, приходящаяся на единицу площади мембраны), кг/м².

Рассчитаем поверхностную плотность мембраны:

, (3)

где m – масса мембраны, кг;

h – толщина мембраны, м;

V – объем мембраны, м³;

S – площадь мембраны, м².

Плотность резины ρ=1,5∙10³ кг/м³ .

Тогда поверхностная плотность мембраны:

Волновая скорость мембраны согласно (2):

м/с.

Входное воздействие (удельная сила) f(r,t), м/с² – это сила, действующая на единицу массы струны, которая через известную линейную плотность внешней силы g(x,t), Н/м определяется через линейную плотность:

. (4)

С учетом известных значений, имеем:

(5)

Начальные условия представлены в виде:

- начальное смещение струны:

(6)

- начальная скорость струны:

. (7)

Имеются граничные условия вида:

; (8)

. (9)

Для выбранного уравнения гиперболического типа стандартизирующая функция имеет вид:

(10)

С учётом входного воздействия (5), принятых начальных (6),(7) и граничных (8),(9) условий стандартизирующая функция принимает вид:

. (11)

Функция Грина:

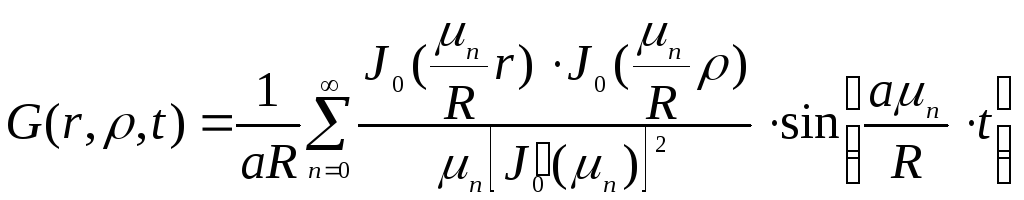. (12)

Передаточная функция:

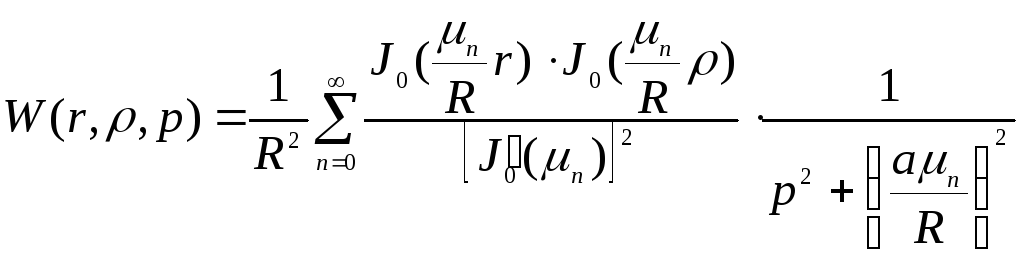. (13)

2. Расчёт выходной распределенной величины

Идентификация исходного уравнения позволяет перейти к расчету распределенной выходной величины, являющейся функцией как пространственной, так и временной координаты и рассчитываемой как пространственно-временная композиция от произведения функции Грина и стандартизирующей функции:

. (14)

Выходная распределенная величина Q(r,t) находится как сумма двух составляющих:

Q(r,t)=Q₁(r,t) + Q₂(r,t), (15)

где Q₁(r,t) и Q₂(r,t) – первая и вторая составляющие выходной величины, определяемые согласно выражениям:

(16)

(17)

Рассчитаем отдельно каждую составляющую решения.

Первая составляющая решения выходной функции:

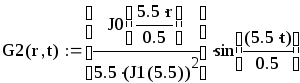
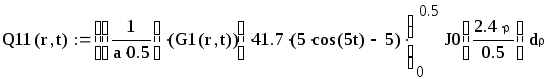
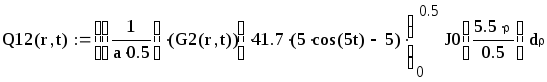
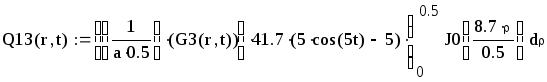
Вторая составляющая решения выходной функции:

.

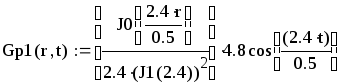
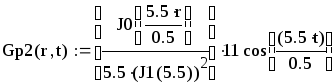
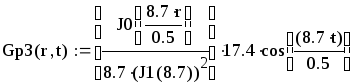
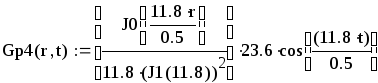
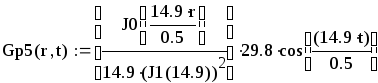
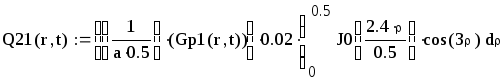
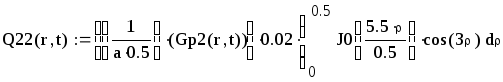
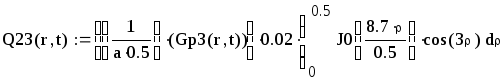
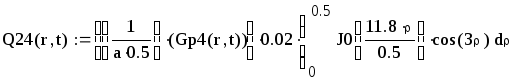
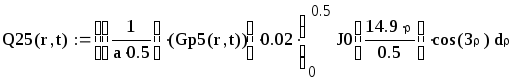
Выходная величина, в результате суммирования двух составляющих решения:

(19)

Как видно из выражения (19) она является функцией двух аргументов: пространственной координаты r и временной координаты t. Построим график этой функции при фиксированном времени t при помощи программы MathCAD.

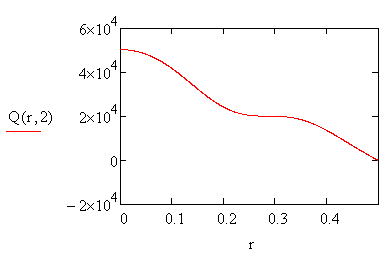
Рисунок 1.2 – График выходной величины Q(r,t) при t=2с